I 5 numere complexe. Ghid de studiu: numere complexe. Numere complexe în formă algebrică

AGENȚIA FEDERALĂ PENTRU EDUCAȚIE

INSTITUȚIE DE ÎNVĂȚĂMÂNT DE STAT

ÎNVĂŢĂMÂNT PROFESIONAL SUPERIOR

„UNIVERSITATEA PEDAGOGICĂ DE STAT VORONEZH”

SCAUN DE AGLEBRA SI GEOMETRIE

Numere complexe

(sarcini selectate)

LUCRARE DE CALIFICARE FINALA

specialitatea 050201.65 matematica

(cu specialitatea suplimentară 050202.65 informatică)

Completat de: student anul 5

fizice si matematice

facultate

Consilier stiintific:

VORONEZH - 2008

1. Introducere……………………………………………………...…………..…

2. Numere complexe (probleme selectate)

2.1. Numere complexe în formă algebrică….……………….….

2.2. Interpretarea geometrică a numerelor complexe…………..…

2.3. Forma trigonometrică a numerelor complexe

2.4. Aplicarea teoriei numerelor complexe la soluționarea ecuațiilor de gradul 3 și 4 ………………………………………………………………………………

2.5. Numere și parametri complexi………………………...….

3. Concluzie………………………………………………………………………………

4. Lista referințelor………………………………………………………………………………

1. Introducere

În programul de matematică curs şcolar teoria numerelor este introdusă pe exemple de mulțimi de numere naturale, întregi, raționale, iraționale, i.e. pe multimea numerelor reale ale caror imagini umplu intreaga linie numerica. Dar deja în clasa a VIII-a nu există suficient stoc de numere reale, rezolvând ecuații patratice cu un discriminant negativ. Prin urmare, a fost necesară completarea stocului de numere reale cu numere complexe pentru care rădăcina pătrată a număr negativ are sensul.

Alegerea temei „Numere complexe”, ca subiect al lucrării mele de calificare finală, este că conceptul de număr complex extinde cunoștințele studenților despre sisteme numerice, despre rezolvarea unei clase largi de probleme atât de conținut algebric, cât și geometric, despre rezolvarea ecuații algebrice orice grad si despre rezolvarea problemelor cu parametri.

În această lucrare de teză este luată în considerare soluția a 82 de probleme.

Prima parte a secțiunii principale „Numere complexe” conține soluții la problemele cu numere complexeîn formă algebrică, se definesc operațiile de adunare, scădere, înmulțire, împărțire, operația de conjugare pentru numere complexe în formă algebrică, gradul unității imaginare, modulul unui număr complex și se precizează și regula extracției. rădăcină pătrată dintr-un număr complex.

În a doua parte se rezolvă probleme de interpretare geometrică a numerelor complexe sub formă de puncte sau vectori ai planului complex.

Partea a treia tratează operațiile cu numere complexe în formă trigonometrică. Se folosesc formule: De Moivre și extragerea unei rădăcini dintr-un număr complex.

A patra parte este dedicată rezolvării ecuațiilor de gradul 3 și 4.

La rezolvarea problemelor ultimei părți „Numere și parametri complexe”, se utilizează și se consolidează informațiile date în părțile anterioare. O serie de probleme din acest capitol este dedicată determinării familiilor de drepte în plan complex dat de ecuații (inegalități) cu un parametru. În parte a exercițiilor, trebuie să rezolvați ecuații cu un parametru (peste câmpul C). Există sarcini în care o variabilă complexă satisface simultan o serie de condiții. O caracteristică a rezolvării problemelor din această secțiune este reducerea multora dintre ele la rezolvarea ecuațiilor (inegalități, sisteme) de gradul doi, iraționale, trigonometrice cu un parametru.

O caracteristică a prezentării materialului fiecărei părți este intrarea inițială fundamente teoretice, iar ulterior aplicarea lor practică în rezolvarea problemelor.

La sfârșitul teza este prezentată o listă a literaturii utilizate. În majoritatea acestora, materialul teoretic este prezentat suficient de detaliat și într-un mod accesibil, sunt luate în considerare soluțiile unor probleme și sarcini practice pentru o soluție independentă. Aș dori să acord o atenție deosebită unor surse precum:

1. Gordienko N.A., Belyaeva E.S., Firstov V.E., Serebryakova I.V. Numerele complexe și aplicațiile lor: Tutorial. . Materialul manualului este prezentat sub formă de prelegeri și exercitii practice.

2. Shklyarsky D.O., Chentsov N.N., Yaglom I.M. Probleme și teoreme alese ale matematicii elementare. Aritmetică și algebră. Cartea conține 320 de probleme legate de algebră, aritmetică și teoria numerelor. Prin natura lor, aceste sarcini diferă semnificativ de standard sarcinile școlare.

2. Numere complexe (probleme selectate)

2.1. Numere complexe în formă algebrică

Rezolvarea multor probleme din matematică și fizică se reduce la rezolvarea ecuațiilor algebrice, adică. ecuații ale formei

unde a0 , a1 , …, an sunt numere reale. Prin urmare, studiul ecuațiilor algebrice este unul dintre probleme criticeîn matematică. De exemplu, o ecuație pătratică cu un discriminant negativ nu are rădăcini reale. Cea mai simplă astfel de ecuație este ecuația

Pentru ca această ecuație să aibă o soluție, este necesar să extindem mulțimea numerelor reale adăugând la aceasta rădăcina ecuației

Să notăm această rădăcină ca

prin urmare,

Expresia rezultată a fost numită numere complexe deoarece conțineau atât părți reale, cât și imaginare.

Deci, numerele complexe se numesc expresii ale formei

Numerele complexe ale formei

Numerele complexe ale formei

Notarea algebrică a numerelor complexe face posibilă efectuarea de operații asupra lor conform regulilor obișnuite ale algebrei.

Suma a două numere complexe

Produsul a două numere complexe

Planul lecției.

1. Moment organizatoric.

2. Prezentarea materialului.

3. Tema pentru acasă.

4. Rezumând lecția.

În timpul orelor

I. Moment organizatoric.

II. Prezentarea materialului.

Motivația.

Setați extinderea numere reale constă în faptul că la numerele reale se adaugă numere noi (imaginare). Introducerea acestor numere este legată de imposibilitatea extragerii rădăcinii dintr-un număr negativ din mulțimea numerelor reale.

Introducerea conceptului de număr complex.

Numerele imaginare cu care suplimentăm numerele reale se scriu ca bi, Unde i este unitatea imaginară și i 2 = - 1.

Pe baza acesteia, obținem următoarea definiție a unui număr complex.

Definiție. Un număr complex este o expresie a formei a+bi, Unde AȘi b sunt numere reale. În acest caz, sunt îndeplinite următoarele condiții:

a) Două numere complexe a 1 + b 1 iȘi a 2 + b 2 i egal dacă și numai dacă a 1 = a 2, b1=b2.

b) Adunarea numerelor complexe este determinată de regula:

(a 1 + b 1 i) + (a 2 + b 2 i) = (a 1 + a 2) + (b 1 + b 2) i.

c) Înmulțirea numerelor complexe este determinată de regula:

(a 1 + b 1 i) (a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (a 1 b 2 - a 2 b 1) i.

Forma algebrică a unui număr complex.

Scrierea unui număr complex în formă a+bi se numește forma algebrică a unui număr complex, unde A- parte reală bi este partea imaginară și b este un număr real.

Număr complex a+bi este considerat egal cu zero dacă părțile sale reale și imaginare sunt egale cu zero: a=b=0

Număr complex a+bi la b = 0 considerat a fi un număr real A: a + 0i = a.

Număr complex a+bi la a = 0 se numește pur imaginar și se notează bi: 0 + bi = bi.

Două numere complexe z = a + biȘi = a – bi, care diferă doar prin semnul părții imaginare, se numesc conjugate.

Acțiuni asupra numerelor complexe în formă algebrică.

Următoarele operații pot fi efectuate pe numere complexe în formă algebrică.

1) Adăugarea.

Definiție. Suma numerelor complexe z 1 = a 1 + b 1 iȘi z 2 = a 2 + b 2 i numit număr complex z, a cărui parte reală este egală cu suma părților reale z1Și z2, iar partea imaginară este suma părților imaginare ale numerelor z1Și z2, acesta este z = (a 1 + a 2) + (b 1 + b 2)i.

Numerele z1Și z2 se numesc termeni.

Adunarea numerelor complexe are următoarele proprietăți:

1º. Comutativitate: z1 + z2 = z2 + z1.

2º. Asociativitate: (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3).

3º. Număr complex -a -bi se numește opusul unui număr complex z = a + bi. Număr complex opus numărului complex z, notat -z. Suma numerelor complexe zȘi -z este egal cu zero: z + (-z) = 0

Exemplul 1: Adăugați (3 - i) + (-1 + 2i).

(3 - i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.

2) Scăderea.

Definiție. Scăderea din numărul complex z1 număr complex z2 z, Ce z + z 2 = z 1.

Teorema. Diferența numerelor complexe există și, în plus, este unică.

Exemplul 2: Scăderea (4 - 2i) - (-3 + 2i).

(4 - 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) i = 7 - 4i.

3) Înmulțirea.

Definiție. Produsul numerelor complexe z 1 =a 1 +b 1 iȘi z 2 \u003d a 2 + b 2 i numit număr complex z, definit prin egalitate: z = (a 1 a 2 – b 1 b 2) + (a 1 b 2 + a 2 b 1)i.

Numerele z1Și z2 se numesc factori.

Înmulțirea numerelor complexe are următoarele proprietăți:

1º. Comutativitate: z 1 z 2 = z 2 z 1.

2º. Asociativitate: (z 1 z 2)z 3 = z 1 (z 2 z 3)

3º. Distributivitatea înmulțirii în raport cu adunarea:

(z 1 + z 2) z 3 \u003d z 1 z 3 + z 2 z 3.

4º. z \u003d (a + bi) (a - bi) \u003d a 2 + b 2 este un număr real.

În practică, înmulțirea numerelor complexe se realizează după regula înmulțirii sumei cu suma și separării părților reale și imaginare.

În exemplul următor, luați în considerare înmulțirea numerelor complexe în două moduri: prin regulă și prin înmulțirea sumei cu suma.

Exemplul 3: Înmulțiți (2 + 3i) (5 – 7i).

1 cale. (2 + 3i) (5 – 7i) = (2× 5 – 3× (- 7)) + (2× (- 7) + 3× 5)i = = (10 + 21) + (- 14 + 15 )i = 31 + i.

2 sensuri. (2 + 3i) (5 - 7i) = 2× 5 + 2× (- 7i) + 3i× 5 + 3i× (- 7i) = = 10 - 14i + 15i + 21 = 31 + i.

4) Diviziune.

Definiție. Împărțiți un număr complex z1 la un număr complex z2, înseamnă a găsi un număr atât de complex z, Ce z z 2 = z 1.

Teorema. Coeficientul numerelor complexe există și este unic dacă z2 ≠ 0 + 0i.

În practică, câtul numerelor complexe se găsește prin înmulțirea numărătorului și numitorului cu conjugatul numitorului.

Lăsa z 1 = a 1 + b 1 i, z 2 = a 2 + b 2 i, Apoi

.

În exemplul următor, efectuăm împărțirea după formula și regula înmulțirii cu conjugatul numitorului.

Exemplul 4. Găsiți un coeficient .

5) Ridicarea la un întreg grad pozitiv.

a) Puterile unitatii imaginare.

Profitând de egalitate i 2 \u003d -1, este ușor de definit orice putere întreagă pozitivă a unității imaginare. Avem:

i 3 \u003d i 2 i \u003d -i,

i 4 \u003d i 2 i 2 \u003d 1,

i 5 \u003d i 4 i \u003d i,

i 6 \u003d i 4 i 2 \u003d -1,

i 7 \u003d i 5 i 2 \u003d -i,

i 8 = i 6 i 2 = 1 etc.

Aceasta arată că gradul valorează eu n, Unde n- întreg număr pozitiv, se repetă periodic cu o creștere a indicatorului cu 4 .

Prin urmare, pentru a crește numărul i la o putere întreagă pozitivă, împărțiți exponentul la 4 și erectă i la puterea al cărei exponent este restul diviziunii.

Exemplul 5 Calculați: (i 36 + i 17) i 23.

i 36 = (i 4) 9 = 1 9 = 1,

i 17 = i 4 × 4+1 = (i 4) 4 × i = 1 i = i.

i 23 = i 4 × 5+3 = (i 4) 5 × i 3 = 1 i 3 = - i.

(i 36 + i 17) i 23 \u003d (1 + i) (- i) \u003d - i + 1 \u003d 1 - i.

b) Ridicarea unui număr complex la o putere întreagă pozitivă se realizează conform regulii ridicării unui binom la puterea corespunzătoare, deoarece este un caz special de înmulțire a factorilor complecși identici.

Exemplul 6 Calculați: (4 + 2i) 3

(4 + 2i) 3 = 4 3 + 3× 4 2 × 2i + 3× 4× (2i) 2 + (2i) 3 = 64 + 96i – 48 – 8i = 16 + 88i.

Numerele complexe sunt o extensie minimă a mulțimii de numere reale cunoscute nouă. Diferența lor fundamentală este că apare un element care la pătrat dă -1, adică. eu, sau.

Orice număr complex are două părți: reale și imaginare:

Astfel, este clar că mulțimea numerelor reale coincide cu mulțimea numerelor complexe cu parte imaginară zero.

Cel mai popular model pentru mulțimea de numere complexe este planul obișnuit. Prima coordonată a fiecărui punct va fi partea sa reală, iar a doua - imaginară. Atunci rolul numerelor complexe în sine vor fi vectori cu începutul în punctul (0,0).

Operații pe numere complexe.

De fapt, dacă luăm în considerare modelul mulțimii numerelor complexe, este intuitiv clar că adunarea (scăderea) și înmulțirea a două numere complexe se realizează în același mod ca și operațiile corespunzătoare pe vectori. Mai mult, ne referim la produsul încrucișat al vectorilor, deoarece rezultatul acestei operații este din nou un vector.

1.1 Adăugarea.

(După cum puteți vedea, această operație corespunde exact cu )

1.2 Scăderea, în mod similar, se realizează conform următoarei reguli:

2. Înmulțirea.

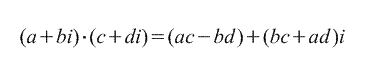
3. Diviziune.

Este definită pur și simplu ca operația inversă de înmulțire.

formă trigonometrică.

Modulul unui număr complex z este următoarea mărime:

,

este evident că acesta, din nou, este pur și simplu modulul (lungimea) vectorului (a,b).

Cel mai adesea, modulul unui număr complex este notat ca ρ.

Se pare că

z = ρ(cosφ+isinφ).

Următoarele decurg direct din forma trigonometrică a scrierii unui număr complex. formule :

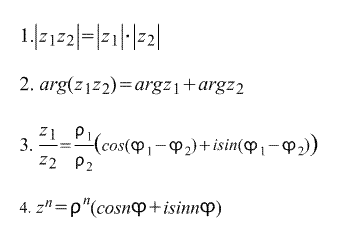
Ultima formulă se numește Formula De Moivre. Formula este derivată direct din ea. a n-a rădăcină a unui număr complex:

astfel, există n-a rădăcini ale numărului complex z.