Rozdelenie gama je matematickým očakávaním. Distribúcia gama a distribúcia Erlang. Stanovenie distribučnej funkcie ukazovateľov spoľahlivosti na základe výsledkov spracovania štatistických informácií

ZÁKLADNÉ ZÁKONY DISTRIBÚCIE KONTINUÁLNYCH NÁHODNÝCH PREMENNÝCH

Hzákon normálneho rozdelenia a jeho význam v teórii pravdepodobnosti. Logaritmicky normálny zákon. Distribúcia gama. Exponenciálny zákon a jeho využitie v teórii spoľahlivosti, teória radenia. Rovnaké právo. distribúcia. Študentská distribúcia. Fisherova distribúcia.

1. Zákon normálneho rozdelenia (Gaussov zákon).

Hustota pravdepodobnosti normálne rozloženej náhodnej premennej je vyjadrená vzorcom:

. (8.1)

Na obr. 16 znázorňuje distribučnú krivku. Je symetrický o

Ryža. 16 Obr. 17

bodov (maximálny bod). Pri znižovaní sa ordináta maximálneho bodu neobmedzene zvyšuje. V tomto prípade je krivka proporcionálne sploštená pozdĺž osi x, takže jej plocha pod grafom zostáva rovná jednotke (obr. 17).

Zákon normálneho rozdelenia je v praktických problémoch veľmi rozšírený. Ljapunov ako prvý vysvetlil dôvody širokého rozšírenia zákona o normálnom rozdeľovaní. Ukázal, že ak možno náhodnú premennú považovať za súčet Vysoké číslo malé termíny, potom za dosť všeobecné podmienky zákon rozdelenia tejto náhodnej veličiny je blízky normálu, bez ohľadu na to, aké sú zákony rozdelenia jednotlivých členov. A keďže prakticky náhodné premenné sú vo väčšine prípadov výsledkom veľkého množstva rôznych príčin, ukazuje sa, že najbežnejším distribučným zákonom je normálny zákon (viac o tom pozri v kapitole 9). Označme číselné charakteristiky normálne rozloženej náhodnej premennej:

Teda parametre a vo vyjadrení (8.1) zákona normálneho rozdelenia sú očakávaná hodnota a štandardná odchýlka náhodnej premennej. Berúc do úvahy túto skutočnosť, vzorec (8.1) možno prepísať takto:

Tento vzorec ukazuje, že zákon normálneho rozdelenia je úplne určený matematickým očakávaním a rozptylom náhodnej premennej. Matematické očakávanie a rozptyl teda úplne charakterizujú normálne rozloženú náhodnú premennú. Je samozrejmé, že vo všeobecnom prípade, keď povaha distribučného zákona nie je známa, znalosť matematického očakávania a rozptylu nestačí na určenie tohto distribučného zákona.

Príklad 1. Vypočítajte pravdepodobnosť, že normálne rozložená náhodná premenná spĺňa nerovnosť.

Riešenie. Pomocou vlastnosti 3 hustoty pravdepodobnosti (kapitola 4, časť 4) dostaneme:

kde je Laplaceova funkcia (pozri prílohu 2).

Urobme nejaké numerické výpočty. Ak dáme , za podmienok príkladu 1, potom

Posledný výsledok znamená, že s pravdepodobnosťou blízkou jednej () náhodná premenná, ktorá sa riadi zákonom normálneho rozdelenia, neprekročí interval . Toto vyhlásenie sa nazýva tri sigma pravidlá.

Nakoniec, ak , , potom náhodná premenná rozdelená podľa normálneho zákona s takýmito parametrami sa nazýva štandardizovaná normálna premenná. Na obr. 18 je znázornený graf hustoty pravdepodobnosti tejto hodnoty .

2. Logaritmicky normálne rozdelenie.

O náhodnej premennej sa hovorí, že má log-normálne rozdelenie (skrátene lognormálne rozdelenie) ak je jeho logaritmus normálne rozdelený, t.j

kde hodnota má normálne rozdelenie s parametrami , .

Hustota lognormálneho rozdelenia je daná nasledujúcim vzorcom:

, .

Matematické očakávanie a rozptyl sú určené vzorcami

Distribučná krivka je znázornená na obr. 19.

Log-normálne rozdelenie sa vyskytuje pri množstve technických problémov. Udáva rozloženie veľkostí častíc pri drvení, rozloženie obsahov prvkov a minerálov vo vyvrelých horninách, rozloženie hojnosti rýb v mori atď. Nachádza sa vo všetkých

tie problémy, kde logaritmus uvažovaného množstva môže byť reprezentovaný ako súčet veľkého počtu nezávislých rovnomerne malých veličín:

t.j. , kde sú nezávislé.

Najjednoduchším druhom gama distribúcie je distribúcia s hustotou

Kde - parameter posunu, - funkcia gama, t.j.

(2)

Každá distribúcia môže byť "rozšírená" do rodiny s posunom škály. V skutočnosti pre náhodnú premennú s distribučnou funkciou zvážte rodinu náhodných premenných , kde je parameter scale a je parameter shift. Potom je distribučná funkcia .

Zahrnutím každého rozdelenia s hustotou tvaru (1) do rodiny s posunom škály získame rodinu gama rozdelení prijatú v parametrizácii:

Tu - parameter tvaru, - parameter mierky, - parameter posunu, funkcia gama je daná vzorcom (2).

V literatúre sú aj iné parametrizácie. Takže namiesto parametra sa často používa parameter . Niekedy sa uvažuje o dvojparametrovej rodine s vynechaním parametra posunu, ale so zachovaním parametra mierky alebo jeho analógu, parametra . Pri niektorých aplikovaných problémoch (napríklad pri štúdiu spoľahlivosti technických zariadení) je to opodstatnené, pretože z vecných úvah sa zdá prirodzené predpokladať, že hustota rozdelenia pravdepodobnosti je pozitívna pre kladné hodnoty argument a len pre nich. S týmto predpokladom súvisí dlhodobá diskusia v 80. rokoch o „pridelených ukazovateľoch spoľahlivosti“, nad ktorou sa nebudeme zdržiavať.

Konkrétne prípady gama distribúcie pre určité hodnoty parametrov majú špeciálne názvy. V , máme exponenciálne rozdelenie. Ak je gama distribúcia prirodzená, je to Erlangovo rozdelenie, ktoré sa používa najmä v teórii radenia. Ak má náhodná premenná gama rozdelenie s parametrom tvaru tak, že - celé číslo a, potom má chí-kvadrát rozdelenie so stupňami voľnosti.

Aplikácie gama distribúcie

Distribúcia gama má široké uplatnenie v rôznych oblastiach technických vied (najmä v spoľahlivosti a teórii testov), v meteorológii, medicíne a ekonómii. Podriadiť možno najmä celkovú životnosť výrobku, dĺžku reťazca vodivých prachových častíc, čas dosiahnutia medzného stavu výrobku pri korózii, prevádzkovú dobu do k-tej poruchy a pod. gama distribúciu. . Stredná dĺžka života pacientov s chronickými ochoreniami, čas na dosiahnutie určitého účinku pri liečbe má v niektorých prípadoch gama distribúciu. Toto rozdelenie sa ukázalo ako najvhodnejšie pre popis dopytu v mnohých ekonomických a matematických modeloch riadenia zásob.

Možnosť využitia gama distribúcie v množstve aplikovaných problémov môže byť niekedy odôvodnená vlastnosťou reprodukovateľnosti: súčet nezávislých exponenciálne rozdelených náhodných premenných s rovnakým parametrom má gama distribúciu s tvarovými a mierkovými parametrami. a posun. Preto sa gama rozdelenie často používa v aplikáciách, kde sa používa exponenciálne rozdelenie.

Stovky publikácií sú venované rôznym otázkam štatistickej teórie súvisiacej s gama distribúciou (pozri zhrnutia). V tomto článku, ktorý si nenárokuje byť komplexný, sa zaoberáme len niektorými matematickými a štatistickými problémami súvisiacimi s vývojom štátnej normy.

Zvážte rozdelenie Gamma, vypočítajte jeho matematické očakávanie, rozptyl, režim. Pomocou funkcie MS EXCEL GAMMA.DIST() vykreslíme distribučnú funkciu a grafy hustoty pravdepodobnosti. Poďme vygenerovať pole náhodných čísel a odhadnúť parametre rozdelenia.

Rozdelenie gama(Angličtina) Gammadistribúcia) závisí od 2 parametrov: r(definuje tvar rozloženia) a λ (definuje mierku). toto rozdelenie je dané nasledujúcim vzorcom:

kde Г(r) je funkcia gama:

ak r je kladné celé číslo, potom Г(r)=(r-1)!

Vyššie uvedený vstupný formulár hustota distribúcie jasne ukazuje svoj vzťah s. Pre r=1 Rozdelenie gama vrie do exponenciálne rozdelenie s parametrom λ.

Ak je parameter λ celé číslo, potom Rozdelenie gama je suma r nezávislé a rovnomerne rozdelené exponenciálny zákon s parametrom λ náhodných veličín X. Takže náhodná premenná r= X 1 + X 2 +… x r Má gama distribúcia s parametrami r a λ.

, zasa úzko súvisí s diskrétnym . Ak Poissonovo rozdelenie popisuje počet náhodných udalostí, ktoré sa vyskytli v určitom časovom intervale, teda exponenciálne rozdelenie, v tomto prípade popisuje dĺžku časového intervalu medzi dvoma po sebe nasledujúcimi udalosťami.

Z toho vyplýva, že ak je napríklad čas pred prvou udalosťou opísaný o exponenciálne rozdelenie s parametrom λ, potom je opísaný čas, kým nastane druhá udalosť gama distribúcia s r = 2 a rovnakým parametrom λ.

Gamma distribúcia v MS EXCEL

V MS EXCEL je prijatá ekvivalentná, ale iná forma zápisu hustota gama distribúcia.

Parameter α ( alfa) je ekvivalentný parametru r a parameter b (beta) - parameter 1/A. Nižšie sa budeme držať práve takéhoto zápisu, pretože to uľahčí písanie vzorcov.

V MS EXCEL, počnúc verziou 2010, pre Distribúcia Gamma existuje funkcia GAMMA.DIST(), anglický názov- GAMMA.DIST(), ktorý vám umožňuje vypočítať hustota pravdepodobnosti(pozri vzorec vyššie) a (pravdepodobnosť, že náhodná premenná X má gama distribúcia, nadobúda hodnotu menšiu alebo rovnú x).

Poznámka: Pred MS EXCEL 2010 mal EXCEL funkciu GAMMADIST(), ktorá vám umožňuje vypočítať integrálna distribučná funkcia A hustota pravdepodobnosti. GAMMADIST() je ponechaný v MS EXCEL 2010 kvôli kompatibilite.

Grafy funkcií

Vzorový súbor obsahuje grafy hustota rozdelenia pravdepodobnosti A integrálna distribučná funkcia.

Rozdelenie gama má označenie Gamma (alfa; beta).

Poznámka: Pre pohodlie pri zapisovaní vzorcov do vzorového súboru pre parametre rozdelenia alfa a beta vytvorené zodpovedajúce .

Poznámka: Závislosť na 2 parametroch umožňuje stavať rozvody rôznych tvarov, čo rozširuje uplatnenie tohto rozvodu. Rozdelenie gama, Páči sa mi to Exponenciálna distribúciačasto sa používa na výpočet čakacej doby medzi náhodné udalosti. Okrem toho je možné túto distribúciu použiť na modelovanie zrážok a návrh ciest.

Ako je uvedené vyššie, ak parameter alfa= 1, potom sa funkcia GAMMA.DIST() vráti s parametrom 1/beta. Ak parameter beta= 1, funkcia GAMMA.DIST() vráti štandard gama distribúcia.

Poznámka: Pretože je špeciálny prípad gama distribúcia, potom vzorec =GAMMA.DIST(x,n/2,2,PRAVDA) pre kladné celé číslo n vráti rovnaký výsledok ako vzorec =XI2.DIST(x; n; TRUE) alebo =1-XI2.DIST.X(x;n) . A vzorec =GAMMA.DIST(x,n/2;2;FALSE) vráti rovnaký výsledok ako vzorec =XI2.DIST(x; n; FALSE), t.j. hustota pravdepodobnosti distribúcie XI2.

IN vzorový súbor na hárku grafiky je uvedený výpočet gama distribúcia rovný alfa*beta A

Rovnomerné rozdelenie. spojitá hodnota X je rovnomerne rozložené v intervale ( a, b) ak sú všetky jeho možné hodnoty v tomto intervale a hustota rozdelenia pravdepodobnosti je konštantná:

Pre náhodnú premennú X, rovnomerne rozložené v intervale ( a, b) (obr. 4), pravdepodobnosť pádu do ľubovoľného intervalu ( X 1 , X 2) ležiace vo vnútri intervalu ( a, b), rovná sa:

(30)

Ryža. 4. Graf hustoty rovnomerného rozdelenia

Chyby zaokrúhľovania sú príklady rovnomerne rozdelených veličín. Ak sú teda všetky tabuľkové hodnoty určitej funkcie zaokrúhlené na rovnakú číslicu, potom náhodným výberom tabuľkovej hodnoty považujeme za zaokrúhľovaciu chybu zvoleného čísla náhodnú premennú rovnomerne rozloženú v intervale.

exponenciálne rozdelenie. Spojitá náhodná premenná X Má exponenciálne rozdelenie

(31)

Graf hustoty rozdelenia pravdepodobnosti (31) je znázornený na obr. 5.

Ryža. 5. Graf hustoty exponenciálneho rozdelenia

Čas T bezporuchovosť počítačového systému je náhodná veličina, ktorá má exponenciálne rozdelenie s parametrom λ , fyzický významčo je priemerný počet porúch za jednotku času, bez odstávok systému na opravy.

Normálne (Gaussovo) rozdelenie. Náhodná hodnota X Má normálne (gaussovské) rozdelenie, ak je rozdelenie hustoty jeho pravdepodobností určené závislosťou:

(32)

Kde m = M(X) , .

o normálne rozdelenie sa nazýva štandardné.

Graf hustoty normálneho rozdelenia (32) je znázornený na obr. 6.

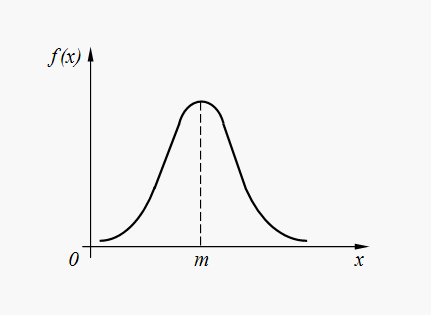
Ryža. 6. Graf hustoty normálneho rozdelenia

Normálne rozdelenie je najbežnejším rozdelením v rôznych náhodných javoch prírody. Takže chyby pri vykonávaní príkazov automatizovaným zariadením, výstupné chyby vesmírna loď k danému bodu v priestore, chyby v parametroch počítačových systémov a pod. vo väčšine prípadov majú normálne alebo blízke normálne rozdelenie. Navyše náhodné premenné tvorené súčtom Vysoké číslo náhodné pojmy sú rozdelené takmer podľa normálneho zákona.

Distribúcia gama. Náhodná hodnota X Má gama distribúcia, ak je rozdelenie hustoty jeho pravdepodobností vyjadrené vzorcom:

(33)

Kde je Eulerova gama funkcia.

PRAX APLIKÁCIE GAMA DISTRIBÚCIE TEÓRIA SPOĽAHLIVOSTI TECHNICKÝCH SYSTÉMOV

Ruslan Litvinenko

kandidát technických vied, docent na subkatedre elektrotechnických komplexov a systémov Kazanskej štátnej energetickej univerzity,

Rusko,tatárska republika,Kazaň

Aleksandr Jamshhikov

magisterský študent,

Rusko,tatárska republika,Kazaň

Aleksej Bagajev

magisterský študentKazanská štátna energetická univerzita,

Rusko,tatárska republika,Kazaň

ANOTÁCIA

V praxi prevádzkovania technických systémov sa vo väčšine prípadov musíme zaoberať pravdepodobnostnými (náhodnými) procesmi, keď funkcia s určitou pravdepodobnosťou odráža argument. V podmienkach neistoty informácií o zákone rozdelenia času vzniku porúch v dôsledku malých objemov štatistických údajov, čo sa zvyčajne deje na skoré štádia vývoj technológie, výskumník sa musí rozhodnúť o výbere a priori modelu spoľahlivosti na základe skúseností z predchádzajúcej prevádzky prototypov alebo analógov. Systematizácia informácií o praktickom využití základných rozdelení pri predpovedaní a hodnotení spoľahlivosti rôznych technických systémov je naliehavou vedeckou úlohou.

Predložený materiál je založený na systematizácii informácií publikovaných v literatúre a predstavuje analýzu výsledkov modelových a experimentálne štúdie spoľahlivosť zariadení, ako aj štatistické údaje získané počas prevádzky.

Prezentované teoretické informácie o použití gama rozdelenia v teórii spoľahlivosti môžu byť použité ako prvé priblíženie a podliehajú povinnému spresňovaniu pomocou rôznych kritérií testovania hypotéz, keďže objem štatistických údajov sa počas nasledujúcich testov zvyšuje.

Na uplatnenie zákona o exponenciálnom rozdelení ako každého iného je potrebné mať dostatok dôvodov. Preto môže byť článok užitočný pre výskumníkov v počiatočných štádiách vývoja alebo modernizácie technického systému ako a priori informácia pre modely budov a kritériá používané na zabezpečenie a kontrolu spoľahlivosti.

ABSTRAKT

V praxi sa prevádzka technických systémov vo väčšine prípadov musí vysporiadať so stochastickými (náhodnými) procesmi, keď funkcia s určitou pravdepodobnosťou odráža argument. Tvárou v tvár neistote o zákone rozloženia času výskytu porúch v dôsledku malého množstva štatistických údajov, čo sa zvyčajne deje v počiatočných fázach vývoja technológie, sa výskumník musí rozhodnúť pre výber spoľahlivosti predchádzajúceho modelu na základe predchádzajúcich prevádzkové skúsenosti s prototypmi alebo analógmi. Systematizácia informácií o praktickom využití základných rozdelení pri predpovedaní a hodnotení spoľahlivosti rôznych technických systémov je dôležitou vedeckou úlohou.

Vo vyššie uvedenom materiáli je systematizácia informácií publikovaných v literatúre a predstavujúca výsledky analýzy modelových a experimentálnych štúdií spoľahlivosti zariadení, ako aj štatistické údaje získané počas prevádzky.

Prezentované teoretické informácie o využití gama distribúcie v teórii spoľahlivosti môžu byť použité ako prvé priblíženie a sú predmetom povinnej špecifikácie s použitím rôznych kritérií testovania hypotéz, čím sa zvyšuje objem štatistických údajov v následných testoch.

Na aplikáciu zákona o exponenciálnom rozdelení ako každého iného je potrebné mať dostatočné dôvody. Preto môže byť článok užitočný pre výskumníkov v počiatočných fázach vývoja alebo modernizácie technických systémov ako a priori informácia na zostavenie modelov a kritérií používaných na zabezpečenie a kontrolu spoľahlivosti.

Kľúčové slová: spoľahlivosť, distribúcia, prevádzkový čas, pravdepodobnosť, hustota, štádium, matematické očakávanie.

Kľúčové slová: spoľahlivosť, distribúcia, prevádzkový čas, pravdepodobnosť, hustota distribúcie, štádium, očakávaná hodnota.

Na popis systémových porúch možno navrhnúť modely na riešenie rôzne úlohy spoľahlivosť a rôznymi spôsobmi zohľadňujú komplex faktorov, ktoré sú vlastné povahe porúch.

Náhodný charakter výskytu porúch pri prevádzke technických systémov a ich prvkov umožňuje uplatniť pri ich popise pravdepodobnostno-štatistické metódy. Najbežnejšie sú modely porúch založené na rozdelení zodpovedajúcich náhodných premenných – času do zlyhania neobnoviteľných objektov a času medzi poruchami obnoviteľných objektov.

Ako hlavné typy distribúcie prevádzkového času produktov do zlyhania je potrebné zdôrazniť:

exponenciálny;
Weibulla-Gnedenko;
gama;
log-normálny;
normálne.

Ako výsledok prehľadu literatúry v oblasti spoľahlivosti technických systémov sa urobilo hodnotenie praktickej aplikácie gama rozdelenia pri štúdiu rôznych technických objektov. Na základe vykonanej analýzy je možné zvoliť vhodné predbežné rozdelenie zodpovedajúceho kritéria alebo ukazovateľa spoľahlivosti.

Rozdelenie gama má dvojparametrovú hustotu s parametrom tvaru a parametrom mierky:

Pravdepodobnosť bezporuchovej prevádzky je určená vzorcom:

Kde: je funkcia gama;

je neúplná funkcia gama.

Matematické očakávania (stredný čas medzi poruchami) a štandardná odchýlka pre gama distribúciu sú:

Vzorec pre mieru zlyhania je nasledujúci:

Rozdelenie gama slúži na opis porúch opotrebovania; poruchy v dôsledku nahromadenia poškodenia; popisy prevádzkového času zložitého technického systému s nadbytočnými prvkami; rozdelenie času na zotavenie; a možno ho použiť aj pri zvažovaní životnosti (zdroja) niektorých technických objektov.

Distribúcia gama má množstvo užitočných vlastností:

Na základe vyššie uvedeného môžeme konštatovať, že gama distribúciu možno použiť vo všetkých oblastiach životného cyklu: zábeh (), normálna prevádzka () a starnutie () .

Na základe , v problémoch, ktoré sú riešené pomocou Laplaceovej transformácie, je vhodné použiť gama rozdelenie na aproximáciu skutočných rozdelení.

B poskytuje nasledujúcu definíciu: gama distribúcia je charakteristika času výskytu porúch v zložitých elektromechanických systémoch v prípadoch, keď sa v počiatočnom štádiu prevádzky alebo v procese ladenia systému vyskytnú okamžité poruchy prvkov, to znamená, že výhodná charakteristika času výskytu porúch zariadenia v procese jeho zábehu.

Pre zložité technické systémy pozostávajúce z prvkov, pre ktoré má pravdepodobnosť bezporuchovej prevádzky exponenciálne rozdelenie, bude mať pravdepodobnosť bezporuchovej prevádzky systému ako celku gama rozdelenie.

Rozdelenie času výskytu porúch zložitého technického systému s náhradnou rezervou (za predpokladu, že poruchové toky hlavného systému a všetkých rezervných prvokov) možno opísať aj gama rozdelením. Podobne, v prípade nezaťaženej alebo zmiešanej redundancie, pravdepodobnosť doby prevádzkyschopnosti systému sleduje zovšeobecnené gama rozdelenie.

Na záver treba poznamenať, že pri riešení jednotlivých problémov sa využívajú aj špeciálne typy (je ich niekoľko desiatok), ako aj diskrétne distribúcie, o ktorých sa v rámci tohto článku neuvažovalo. V tomto prípade dochádza k rôznym vzájomným prechodom a prepojeniam medzi rozvodmi. Napriek existujúcim kritériám zhody medzi zvolenými teoretickými a empirickými rozdeleniami, všetky poskytujú odpoveď na otázku: existujú alebo neexistujú dostatočné dôvody na odmietnutie hypotézy o zvolenom rozdelení? Autori poznamenali, že akékoľvek údaje môžu byť upravené na viacparametrový zákon, aj keď nezodpovedajú skutočným. fyzikálnych javov. Pri výbere typu rozvodu a jeho parametrov je teda potrebné v prvom rade zohľadniť fyzikálnu podstatu prebiehajúcich procesov a dejov.

Bibliografia:

GOST R.27.001-2009. Spoľahlivosť v technológii. modely porúch. – M.: Standartinform, 2010. – 16 s.
Gertsbakh I.B., Kordonsky H.B. Modely porúch / ed. B.V. Gnedenko. - M.: Sovietsky rozhlas, 1966. - 166 s.
Gnedenko B.V. Otázky matematickej teórie spoľahlivosti. - M .: Rádio a komunikácia, 1983. – 376 s.
Kashtanov V.N., Medvedev A.I. Teória spoľahlivosti zložitých systémov: učebnica - M.: FIZMATLIT, 2010. - 609 s.
Litvinenko R.S. Simulačný model procesu fungovania elektrického komplexu, berúc do úvahy spoľahlivosť jeho prvkov // Journal "Nadezhnost". - 2016. - č. 1 (56) - S. 46–54.
Litvinenko R.S., Idiyatullin R.G., Kisneeva L.N. Posúdenie spoľahlivosti hybridného vozidla vo fáze vývoja // Journal "Doprava: veda, technika, manažment". - 2016. - č. 2 - S. 34–40.
Strojárstvo: encyklopédia 40 zväzkov T. IV-3: Spoľahlivosť strojov / V.V. Klyuev, V.V. Bolotin, F.R. Sosnin a ďalší; pod celkom vyd. V.V. Klyuev. – M.: Mashinostroenie, 2003. – 592 s.
Truchanov V.M. Spoľahlivosť technických systémov ako sú mobilné inštalácie v štádiu návrhu a testovania prototypov: vedecká publikácia - M.: Mashinostroenie, 2003. - 320 s.
Khazov B.F., Didusev B.A. Príručka na výpočet spoľahlivosti strojov v štádiu projektovania. – M.: Mashinostroenie, 1986. – 224 s.
Cherkesov G.N. Spoľahlivosť hardvérových a softvérových systémov: učebnica. príspevok. - Petrohrad: Peter, 2005. - 479 s.