I 5 күрделі сандар. Оқу құралы: Күрделі сандар. Алгебралық түрдегі күрделі сандар

ФЕДЕРАЛДЫҚ БІЛІМ БЕРУ АГЕНТІГІ

МЕМЛЕКЕТТІК ОҚУ МЕКЕМЕСІ

ЖОҒАРЫ КӘСІБИ БІЛІМ

«ВОРОНЕЖ МЕМЛЕКЕТТІК ПЕДАГОГИКАЛЫҚ УНИВЕРСИТЕТІ»

АГЛЕБРА ЖӘНЕ ГЕОМЕТРИЯ КАФЕДРАСЫ

Күрделі сандар

(таңдалған тапсырмалар)

ҚОРЫТЫНДЫ БІЛІКТІЛІК ЖҰМЫСЫ

050201.65 математика мамандығы

(050202.65 информатика қосымша мамандығымен)

Орындаған: 5 курс студенті

физикалық және математикалық

факультет

Ғылыми жетекші:

ВОРОНЕЖ – 2008 ж

1. Кіріспе……………………………………………………...…………..…

2. Күрделі сандар (таңдалған есептер)

2.1. Алгебралық түрдегі күрделі сандар………………….….

2.2. Күрделі сандардың геометриялық интерпретациясы………………

2.3. Комплекс сандардың тригонометриялық түрі

2.4. Комплекс сандар теориясын 3 және 4 дәрежелі теңдеулерді шешуге қолдану…………………………………………………………………

2.5. Күрделі сандар мен параметрлер………………………………………

3. Қорытынды……………………………………………………….

4. Пайдаланылған әдебиеттер тізімі……………………………………………

1. Кіріспе

Математика бағдарламасында мектеп курсысандар теориясы натурал сандар, бүтін сандар, рационал, иррационал, т. кескіндері бүкіл сан жолын толтыратын нақты сандар жиынында. Бірақ қазірдің өзінде 8-сыныпта теріс дискриминанты бар квадрат теңдеулерді шешетін нақты сандар қоры жеткіліксіз. Сондықтан нақты сандар қорын квадрат түбірі болатын күрделі сандармен толықтыру қажет болды теріс санмағынасы бар.

«Күрделі сандар» тақырыбын менің қорытынды біліктілік жұмысымның тақырыбы ретінде таңдау мынада: күрделі сан ұғымы студенттердің сандық жүйелер туралы білімдерін кеңейтеді, алгебралық және геометриялық мазмұндағы есептердің кең класын шешу, шешу туралы білімдерін кеңейтеді. алгебралық теңдеулеркез келген дәреже және параметрлері бар есептерді шешу туралы.

Бұл дипломдық жұмыста 82 мәселенің шешімі қарастырылған.

«Күрделі сандар» негізгі бөлімінің бірінші бөлімінде есептердің шешімдері берілген күрделі сандаралгебралық түрде қосу, алу, көбейту, бөлу амалдары, алгебралық түрдегі күрделі сандарға жалғау амалдары, жорамал бірлік дәрежесі, комплекс санның модулі анықталады, сонымен қатар шығару ережесі айтылады. шаршы түбіркүрделі саннан.

Екінші бөлімде комплекс сандарды нүктелер немесе комплекс жазықтықтың векторлары түріндегі геометриялық түсіндіруге арналған есептер шығарылады.

Үшінші бөлімде күрделі сандарға амалдар қарастырылады тригонометриялық пішін. Формулалар қолданылады: Де Моивр және күрделі саннан түбірді алу.

Төртінші бөлім 3 және 4 дәрежелі теңдеулерді шешуге арналған.

«Күрделі сандар мен параметрлер» соңғы бөлімінің есептерін шығару кезінде алдыңғы бөлімдерде берілген мәліметтер пайдаланылады және бекітіледі. Бұл тарауда есептер қатары параметрі бар теңдеулер (теңсіздіктер) арқылы берілген күрделі жазықтықтағы түзулердің отбасыларын анықтауға арналған. Жаттығулардың бір бөлігінде параметрі бар теңдеулерді шешу керек (С өрісінің үстінде). Күрделі айнымалы бірнеше шарттарды бір уақытта қанағаттандыратын тапсырмалар бар. Бұл бөлімнің есептерін шешудің ерекшелігі олардың көпшілігін екінші дәрежелі, иррационал, параметрі бар тригонометриялық теңдеулерді (теңсіздіктер, жүйелер) шешуге келтіру болып табылады.

Әрбір бөліктің материалын ұсыну ерекшелігі бастапқы енгізу болып табылады теориялық негіздері, кейінірек оларды есептерді шешуде практикалық қолдану.

Соңында дипломдық жұмыспайдаланылған әдебиеттер тізімі берілген. Олардың көпшілігінде теориялық материал жеткілікті түрде егжей-тегжейлі және қолжетімді түрде берілген, кейбір мәселелердің шешімдері қарастырылған және практикалық тапсырмалартәуелсіз шешім үшін. Мынадай көздерге ерекше назар аударғым келеді:

1. Гордиенко Н.А., Беляева Е.С., Фиртов В.Е., Серебрякова И.В. Күрделі сандар және олардың қолданылуы: Оқу құралы. . Әдістемелік нұсқаулықтың материалы лекция және түрінде берілген практикалық жаттығулар.

2. Шклярский Д.О., Ченцов Н.Н., Яглом И.М. Элементар математиканың таңдамалы есептері мен теоремалары. Арифметика және алгебра. Кітапта алгебра, арифметика және сандар теориясына қатысты 320 есеп бар. Табиғаты бойынша бұл тапсырмалар стандарттан айтарлықтай ерекшеленеді мектеп тапсырмалары.

2. Күрделі сандар (таңдалған есептер)

2.1. Алгебралық түрдегі күрделі сандар

Математика мен физикадағы көптеген есептерді шешу алгебралық теңдеулерді шешуге дейін қысқарады, яғни. түріндегі теңдеулер

мұндағы a0 , a1 , …, an нақты сандар. Сондықтан алгебралық теңдеулерді зерттеудің бірі сыни мәселелерматематикада. Мысалы, теріс дискриминанты бар квадрат теңдеудің нақты түбірі болмайды. Мұндай теңдеулердің ең қарапайымы теңдеу болып табылады

Бұл теңдеудің шешімі болуы үшін оған теңдеудің түбірін қосу арқылы нақты сандар жиынын кеңейту керек.

Бұл түбірді деп белгілейік

демек,

Алынған өрнек күрделі сандар деп аталды, өйткені оларда нақты және жорамал бөліктер бар.

Сонымен, күрделі сандар форманың өрнектері деп аталады

Пішіннің күрделі сандары

Пішіннің күрделі сандары

Күрделі сандардың алгебралық жазылуы олармен алгебраның әдеттегі ережелері бойынша амалдарды орындауға мүмкіндік береді.

Екі күрделі санның қосындысы

Екі күрделі санның көбейтіндісі

Сабақ жоспары.

1. Ұйымдастыру кезеңі.

2. Материалды таныстыру.

3. Үйге тапсырма.

4. Сабақты қорытындылау.

Сабақтар кезінде

I. Ұйымдастыру кезеңі.

II. Материалды таныстыру.

Мотивация.

Кеңейтуді орнату нақты сандарнақты сандарға жаңа сандар (ойдан алынған) қосылуынан тұрады. Бұл сандарды енгізу нақты сандар жиынындағы теріс саннан түбір алу мүмкін еместігімен байланысты.

Комплекс сан ұғымымен таныстыру.

Нақты сандарды толықтыратын ойша сандар былай жазылады би, Қайда менойша бірлік болып табылады, және i 2 = - 1.

Осының негізінде күрделі санның келесі анықтамасын аламыз.

Анықтама. Күрделі сан – пішіннің өрнегі a+bi, Қайда аЖәне бнақты сандар. Бұл жағдайда келесі шарттар орындалады:

а) Екі күрделі сан a 1 + b 1 iЖәне a 2 + b 2 iтең болса және тек егер a 1 = a 2, b1=b2.

б) Күрделі сандардың қосылуы мына ережемен анықталады:

(a 1 + b 1 i) + (a 2 + b 2 i) = (a 1 + a 2) + (b 1 + b 2) i.

в) Күрделі сандарды көбейту мына ережемен анықталады:

(a 1 + b 1 i) (a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (a 1 b 2 - a 2 b 1) i.

Комплекс санның алгебралық түрі.

Күрделі санды пішінде жазу a+biкүрделі санның алгебралық түрі деп аталады, мұндағы А- нақты бөлігі биқиял бөлігі болып табылады және бнақты сан болып табылады.

Күрделі сан a+biнөлге тең деп есептеледі, егер оның нақты және жорамал бөліктері нөлге тең болса: a=b=0

Күрделі сан a+biсағ b = 0нақты сан болып есептеледі а: a + 0i = a.

Күрделі сан a+biсағ a = 0таза елестету деп аталады және белгіленеді би: 0 + bi = bi.

Екі күрделі сан z = a + biЖәне = а – би, тек қиял бөлігінің таңбасымен ғана ерекшеленетін сыңарлары құрмалас деп аталады.

Алгебралық түрдегі күрделі сандарға әрекеттер.

Алгебралық түрде күрделі сандарға келесі амалдарды орындауға болады.

1) Қосымша.

Анықтама. Күрделі сандардың қосындысы z 1 = a 1 + b 1 iЖәне z 2 = a 2 + b 2 iкүрделі сан деп аталады z, оның нақты бөлігі нақты бөліктерінің қосындысына тең z1Және z2, ал қиял бөлігі сандардың елестетілген бөліктерінің қосындысы болып табылады z1Және z2, яғни z = (a 1 + a 2) + (b 1 + b 2)i.

Сандар z1Және z2терминдер деп аталады.

Күрделі сандарды қосу бар келесі қасиеттер:

1º. Коммутативтілік: z1 + z2 = z2 + z1.

2º. Ассоциативтілік: (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3).

3º. Күрделі сан -а -бикүрделі санға қарама-қарсы сан деп аталады z = a + bi. Күрделі санға қарама-қарсы күрделі сан z, белгіленген -z. Күрделі сандардың қосындысы zЖәне -zнөлге тең: z + (-z) = 0

1-мысал: Қосу (3 - i) + (-1 + 2i).

(3 - i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.

2) Алу.

Анықтама.Күрделі саннан алу z1күрделі сан z2 z,Не z + z 2 = z 1.

Теорема. Күрделі сандардың айырмашылығы бар және оның үстіне бірегей.

2-мысал: Алу (4 - 2i) - (-3 + 2i).

(4 - 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) i = 7 - 4i.

3) Көбейту.

Анықтама. Күрделі сандардың көбейтіндісі z 1 =a 1 +b 1 iЖәне z 2 \u003d a 2 + b 2 iкүрделі сан деп аталады z, теңдігімен анықталады: z = (a 1 a 2 – b 1 b 2) + (a 1 b 2 + a 2 b 1)i.

Сандар z1Және z2факторлар деп аталады.

Күрделі сандарды көбейту келесі қасиеттерге ие:

1º. Коммутативтілік: z 1 z 2 = z 2 z 1.

2º. Ассоциативтілік: (z 1 z 2)z 3 = z 1 (z 2 z 3)

3º. Көбейтудің қосуға қатысты үлестірімділігі:

(z 1 + z 2) z 3 \u003d z 1 z 3 + z 2 z 3.

4º. z \u003d (a + bi) (a - bi) \u003d a 2 + b 2нақты сан болып табылады.

Практикада күрделі сандарды көбейту қосындыны қосындыға көбейту және нақты және жорамал бөлшектерді бөлу ережесі бойынша жүзеге асырылады.

Келесі мысалда күрделі сандарды екі жолмен көбейтуді қарастырайық: ереже бойынша және қосындыны қосындыға көбейту.

3-мысал: Көбейту (2 + 3i) (5 – 7i).

1 жол. (2 + 3i) (5 – 7i) = (2× 5 – 3× (- 7)) + (2× (- 7) + 3× 5)i = = (10 + 21) + (- 14 + 15)i = 31 + i.

2 жол. (2 + 3i) (5 - 7i) = 2× 5 + 2× (- 7i) + 3i× 5 + 3i× (- 7i) = = 10 - 14i + 15i + 21 = 31 + i.

4) Бөлім.

Анықтама. Күрделі санды бөл z1күрделі санға z2, осындай күрделі санды табуды білдіреді z, Не z z 2 = z 1.

Теорема.Күрделі сандардың бөлімі бар және бірегей, егер болса z2 ≠ 0 + 0i.

Практикада күрделі сандардың бөлімі алымы мен бөлімін бөлгіштің жалғауына көбейту арқылы табылады.

Болсын z 1 = a 1 + b 1 i, z 2 = a 2 + b 2 i, Содан кейін

.

Келесі мысалда формула бойынша бөлуді және көбейту ережесін бөлгіштің жалғауы арқылы орындаймыз.

Мысал 4. Бөліндіні табыңыз .

5) Біртұтас етіп көтеру оң дәреже.

а) Елестету бірлігінің күштері.

Теңдікті пайдалану i 2 \u003d -1, ойша бірліктің кез келген оң бүтін дәрежесін анықтау оңай. Бізде бар:

i 3 \u003d i 2 i \u003d -i,

i 4 \u003d i 2 i 2 \u003d 1,

i 5 \u003d i 4 i \u003d i,

i 6 \u003d i 4 i 2 \u003d -1,

i 7 \u003d i 5 i 2 \u003d -i,

i 8 = i 6 i 2 = 1және т.б.

Бұл дәреже мәндерін көрсетеді мен н, Қайда n- тұтас оң сан, көрсеткішінің артуымен мерзімді түрде қайталанады 4 .

Сондықтан санын көбейту меноң бүтін дәрежеге, көрсеткішті мынаға бөліңіз 4 және тұрғызу менкөрсеткіші бөлімнің қалдығы болатын дәрежеге.

5-мысал Есептеңіз: (i 36 + i 17) i 23.

i 36 = (i 4) 9 = 1 9 = 1,

i 17 = i 4 × 4+1 = (i 4) 4 × i = 1 i = i.

i 23 = i 4 × 5+3 = (i 4) 5 × i 3 = 1 i 3 = - i.

(i 36 + i 17) i 23 \u003d (1 + i) (- i) \u003d - i + 1 \u003d 1 - i.

б) Комплекс санды бүтін натурал дәрежеге көтеру биномдық мәнді сәйкес дәрежеге көтеру ережесі бойынша жүзеге асырылады, өйткені бұл бірдей күрделі көбейткіштерді көбейтудің ерекше жағдайы.

6-мысал Есептеңіз: (4 + 2i) 3

(4 + 2i) 3 = 4 3 + 3× 4 2 × 2i + 3× 4× (2i) 2 + (2i) 3 = 64 + 96i – 48 – 8i = 16 + 88i.

Күрделі сандар бізге таныс нақты сандар жиынының минималды кеңейтімі болып табылады. Олардың түбегейлі айырмашылығы мынада: квадрат -1 беретін элемент пайда болады, яғни. i, немесе .

Кез келген күрделі сан екі бөліктен тұрады: нақты және ойдан шығарылған:

Осылайша, нақты сандар жиыны нөлдік елестетілген күрделі сандар жиынымен сәйкес келетіні анық.

Күрделі сандар жиынының ең танымал үлгісі қарапайым жазықтық болып табылады. Әрбір нүктенің бірінші координатасы оның нақты бөлігі, ал екіншісі - елестетілген болады. Сонда комплекс сандардың өздері рөлі басы (0,0) нүктесінде болатын векторлар болады.

Комплекс сандарға амалдар.

Шын мәнінде, күрделі сандар жиынының моделін ескеретін болсақ, екі күрделі санды қосу (алу) мен көбейту векторларға сәйкес амалдар сияқты орындалатыны интуитивті түрде анық болады. Оның үстіне, біз векторлардың көлденең көбейтіндісін айтамыз, өйткені бұл операцияның нәтижесі қайтадан вектор болып табылады.

1.1 Қосымша.

(Көріп тұрғаныңыздай, бұл әрекет дәл сәйкес келеді)

1.2 Алу, сол сияқты, келесі ережеге сәйкес орындалады:

2. Көбейту.

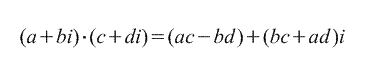
3. Бөлім.

Ол жай ғана көбейтудің кері операциясы ретінде анықталады.

тригонометриялық пішін.

z комплекс санының модулі келесі шама:

,

бұл (a,b) векторының жай ғана модулі (ұзындығы) екені анық.

Көбінесе күрделі санның модулі былай белгіленеді ρ.

Солай екен

z = ρ(cosφ+isinφ).

Төменде күрделі санды жазудың тригонометриялық түрінен тікелей шығады. формулалар :

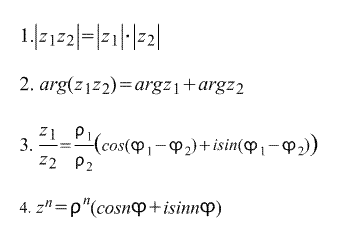
Соңғы формула деп аталады Де Моевр формуласы. Формула одан тікелей алынған. күрделі санның n-ші түбірі:

осылайша, z күрделі санның n-ші түбірлері бар.