Când funcția este continuă într-un punct. Clasificarea punctelor de întrerupere a unei funcții. Proprietățile de bază ale funcțiilor continue

Procesul de studiere a unei funcții pentru continuitate este indisolubil legat de abilitatea de a găsi limite unilaterale ale unei funcții. Prin urmare, pentru a începe studiul materialului acestui articol, este recomandabil să analizați mai întâi subiectul limitei unei funcții.

funcția f(x). este continuuîn punctul x 0 dacă limita din stânga este egală cu limita din dreapta și coincide cu valoarea funcției în punctul x 0 , adică: lim x → x 0 - 0 f (x) = lim x → x 0 + 0 f (x) = f(x0)

Această definiție ne permite să derivăm un corolar: valoarea limitei unei funcții în punctele de continuitate coincide cu valoarea funcției în aceste puncte.

Exemplul 1

Având în vedere o funcție f (x) = 1 6 (x - 8) 2 - 8 . Este necesar să se demonstreze continuitatea acestuia în punctul x 0 = 2.

Soluţie

În primul rând, definim existența unei limite la stânga. Pentru a face acest lucru, folosim o succesiune de argumente x n care se reduce la x 0 = 2 (x n< 2) . Например, такой последовательностью может быть:

2 , 0 , 1 , 1 1 2 , 1 3 4 , 1 7 8 , 1 15 16 , . . . , 1 1023 1024 , . . . → 2

Secvența corespunzătoare de valori ale funcției arată astfel:

f(-2); f(0); f (1) ; f 1 1 2 ; f 1 3 4 ; f 1 7 8 ; f 1 15 16; . . . ; f 1 1023 1024; . . . == 8 . 667; 2. 667; 0 . 167; - 0 . 958; - 1 . 489; - 1 . 747; - 1 . 874; . . . ; - 1 . 998; . . . → - 2

în desen sunt marcate cu verde.

Este destul de evident că o astfel de secvență se reduce la - 2 , deci lim x → 2 - 0 1 6 (x - 8) 2 - 8 = - 2 .

Să definim existența limitei din dreapta: folosim șirul de argumente x n , care se reduce la x 0 = 2 (x n > 2) . De exemplu, o astfel de secvență ar putea fi:

6 , 4 , 3 , 2 1 2 , 2 1 4 , 2 1 8 , 2 1 16 , . . . , 2 1 1024 , . . . → 2

Secvența relevantă de funcții:

f(6) ; f (4); f (3); f 2 1 2 ; f 2 1 4 ; f 2 1 8 ; f 2 1 16 ; . . . ; f211024; . . . == - 7 . 333; - 5 . 333; - 3 . 833; - 2 . 958; - 2 . 489; - 2 . 247; - 2 . 247; - 2 . 124; . . . ; - 2 . 001; . . . → - 2

prezentată cu albastru în figură.

Și această secvență se reduce la - 2 , apoi lim x → 2 + 0 1 6 (x - 8) 2 - 8 = - 2 .

Acțiunile de mai sus au arătat că limitele din dreapta și din stânga sunt egale, ceea ce înseamnă că există o limită a funcției f (x) \u003d 1 6 x - 8 2 - 8 în punctul x 0 \u003d 2, în timp ce lim x → 2 1 6 (x - 8 ) 2 - 8 = - 2 .

După calcularea valorii funcției la un punct dat, următoarea egalitate este evidentă:

lim x → 2 - 0 f (x) = lim x → 2 + 0 f (x) = f (2) = 1 6 (2 - 8) 2 - 8 = - 2 care indică continuitatea funcției date la punct dat.

Să o arătăm grafic:

Răspuns: Se demonstrează continuitatea funcției f (x) = 1 6 (x - 8) 2 - 8 în partea dată.

Discontinuitate detașabilă de primul fel

Funcția are discontinuitate detașabilă de primul felîn punctul x 0, când limitele din dreapta și din stânga sunt egale, dar nu egale cu valoarea funcției din punct, adică:

lim x → x 0 - 0 f (x) = lim x → x 0 + 0 f (x) ≠ f (x 0)

Exemplul 2

Este dată funcția f (x) = x 2 - 25 x - 5. Este necesar să se determine punctele de rupere și să se determine tipul acestora.

Soluţie

În primul rând, notăm domeniul funcției: D (f (x)) ⇔ D x 2 - 25 x - 5 ⇔ x - 5 ≠ 0 ⇔ x ∈ (- ∞ ; 5) ∪ (5 ; + ∞)

Într-o funcție dată, doar punctul limită al domeniului de definiție poate servi ca punct de întrerupere, adică. x 0 = 5. Să examinăm funcția pentru continuitate în acest punct.

Să simplificăm expresia x 2 - 25 x - 5: x 2 - 25 x - 5 \u003d (x - 5) (x + 5) x - 5 \u003d x + 5.

Să definim limitele din dreapta și din stânga. Deoarece funcția g(x) = x + 5 este continuă pentru orice x real, atunci:

lim x → 5 - 0 (x + 5) = 5 + 5 = 10 lim x → 5 + 0 (x + 5) = 5 + 5 = 10

Răspuns: limitele din dreapta și din stânga sunt egale, iar funcția dată în punctul x 0 = 5 nu este definită, adică. în acest moment funcția are o discontinuitate detașabilă de primul fel.

O discontinuitate irecuperabilă de primul fel este determinată și de punctul de salt al funcției.

Definiția 3 Exemplul 3

Având în vedere o funcție continuă pe bucăți f (x) = x + 4 , x< - 1 , x 2 + 2 , - 1 ≤ x < 1 2 x , x ≥ 1 . Необходимо изучить funcţie dată pentru continuitate, desemnați tipul de puncte de întrerupere, întocmește un desen.

Soluţie

Pauzele acestei funcții pot fi numai în punctul x 0 = - 1 sau în punctul x 0 = 1.

Să determinăm limitele la dreapta și la stânga acestor puncte și valoarea funcției date în aceste puncte:

• la stânga punctului x 0 \u003d - 1, funcția dată este f (x) \u003d x + 4, apoi datorită continuității funcție liniară: lim x → - 1 - 0 f (x) = lim x → - 1 - 0 (x + 4) = - 1 + 4 = 3 ;
• direct în punctul x 0 \u003d - 1, funcția ia forma: f (x) \u003d x 2 + 2, apoi: f (- 1) \u003d (- 1) 2 + 2 \u003d 3;
• pe intervalul (- 1 ; 1) funcţia dată este: f (x) = x 2 + 2 . Pe baza proprietății de continuitate a unei funcții pătratice, avem: lim x → - 1 + 0 f (x) = lim x → - 1 + 0 (x 2 + 2) = (- 1) 2 + 2 = 3 lim x → 1 - 0 f (x) = lim x → 1 - 0 (x 2 + 2) = (1) 2 + 2 = 3
• în punctul x 0 \u003d - 1, funcția are forma: f (x) \u003d 2 x și f (1) \u003d 2 1 \u003d 2.
• la dreapta punctului x 0 funcţia dată este f (x) = 2 x . Datorită continuității funcției liniare: lim x → 1 + 0 f (x) = lim x → 1 + 0 (2 x) = 2 1 = 2

Răspuns: am ajuns cu:

• lim x → - 1 - 0 f (x) = lim x → - 1 + 0 f (x) = f (- 1) = 3 - aceasta înseamnă că în punctul x 0 = - 1 funcția dată pe bucăți este continuă;
• lim x → - 1 - 0 f (x) = 3, lim x → 1 + 0 f (x) = 2 - astfel, în punctul x 0 = 1, se definește o discontinuitate inamovibilă de primul fel (salt).

Trebuie doar să pregătim un desen al acestei sarcini.

Funcția are pauză de al doilea felîn punctul x 0, când oricare dintre limitele de pe lim stânga x → x 0 - 0 f (x) sau de pe lim dreapta x → x 0 + 0 f (x) nu există sau este infinită.

Exemplul 4

Este dată funcția f (x) = 1 x. Este necesar să se investigheze funcția dată pentru continuitate, să se determine tipul de puncte de întrerupere și să se pregătească un desen.

Soluţie

Să scriem domeniul funcției: x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) .

Aflați limitele la dreapta și la stânga punctului x 0 = 0.

Să setăm o secvență arbitrară de valori ale argumentelor care converg la x 0 din stânga. De exemplu:

8 ; - 4 ; - 2 ; - 1 ; - 1 2 ; - 1 4 ; . . . ; - 1 1024 ; . . .

Ea corespunde secvenței de valori ale funcției:

f(-8); f(-4); f(-2); f(-1); f - 1 2 ; f - 1 4 ; . . . ; f - 1 1024; . . . = = - 1 8 ; - 14 ; - 12 ; - 1 ; - 2; - 4 ; . . . ; - 1024; . . .

Evident, această succesiune este negativă infinit de mare, atunci lim x → 0 - 0 f (x) = lim x → 0 - 0 1 x = - ∞ .

Acum să definim o secvență arbitrară de valori ale argumentului care converg la x 0 din dreapta. De exemplu: 8 ; 4; 2; 1; 12; 14; . . . ; 1 1024; . . . , și corespunde secvenței de valori ale funcției:

f (8) ; f (4); f (2) ; f (1) ; f 1 2 ; f 1 4 ; . . . ; f 1 1024; . . . == 1 8 ; 14; 12; 1; 2; 4; . . . ; 1024; . . .

Această succesiune este una pozitivă infinit de mare, ceea ce înseamnă că lim x → 0 + 0 f (x) = lim x → 0 + 0 1 x = + ∞ .

Răspuns: punctul x 0 = 0 - punct de discontinuitate a funcţiei de al doilea fel.

Să ilustrăm:

Dacă observați o greșeală în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter

Exemplul #1. Demonstrați că funcția y=sinx este continuă pentru orice valoare a lui x .
Soluţie. Fie x 0 un punct arbitrar. Dându-i un increment Δx, obținem punctul x=x 0 +Δx. Atunci Δy=f(x)-f(x 0) = sin(x 0 +Δx)-sin(x) = . Primim .

Definiție . Funcția y=f(x) se numește continuă în punctul x 0 din dreapta (stânga) dacă
.
O funcție continuă într-un punct interior va fi atât la dreapta cât și la stânga continuă. Este adevărat și invers: dacă o funcție este continuă într-un punct din stânga și din dreapta, atunci va fi continuă în acel punct. Cu toate acestea, funcția poate fi continuă doar pe o parte. De exemplu, pentru , , f(1)=1, prin urmare, această funcție este continuă doar în stânga (pentru graficul acestei funcții, vezi Secțiunea 5.7.2 de mai sus).
Definiție. O funcție se numește continuă pe un anumit interval dacă este continuă în fiecare punct al acestui interval.
În special, dacă intervalul este un segment, atunci continuitatea unilaterală este implicată la capetele sale.

Proprietățile funcțiilor continue

Întreruperile de funcții și clasificarea lor

Următoarea clasificare este acceptată pentru punctele de discontinuitate.
1) Dacă în punctul x 0 sunt finite Și , dar f(x 0 +0)≠f(x 0 -0), atunci x 0 se numește punct de rupere de primul fel , în timp ce ei sună functie de salt .

Exemplul 2 Luați în considerare funcția
Ruperea funcției este posibilă doar în punctul x=2 (în alte puncte este continuă ca orice polinom).
Sa gasim , . Deoarece limitele unilaterale sunt finite, dar nu egale între ele, în punctul x=2 funcția are o discontinuitate de primul fel. observa asta , prin urmare funcția este dreaptă-continuă în acest punct (Fig. 2).
2) Puncte de discontinuitate de al doilea fel sunt numite puncte la care cel puțin una dintre limitele unilaterale este egală cu ∞ sau nu există.

Exemplul 3 Funcția y=2 1/ x este continuă pentru toate valorile lui x, cu excepția x=0. Găsiți limite unilaterale: , , prin urmare x=0 este un punct de discontinuitate de al doilea fel (Fig. 3).
3) Se numește punctul x=x 0 punct de rupere , dacă f(x 0 +0)=f(x 0 -0)≠f(x 0).
Decalajul este „demontabil” în sensul că este suficient să modificați (redefiniți sau redefiniți) valoarea funcției în acest punct prin setarea , iar funcția va deveni continuă în punctul x 0 .
Exemplul 4 Se știe că , iar această limită nu depinde de modul în care x tinde spre zero. Dar funcția în punctul x=0 nu este definită. Dacă extindem definiția funcției prin stabilirea f(0)=1, atunci aceasta se dovedește a fi continuă în acest punct (în alte puncte este continuă ca un coeficient al funcțiilor continue sinx și x).
Exemplul 5 Investigați continuitatea unei funcții .
Soluţie. Funcțiile y=x 3 și y=2x sunt definite și continue peste tot, inclusiv în intervalele indicate. Să examinăm punctul de joncțiune al golurilor x=0:
, , . Obtinem ca , de unde rezulta ca in punctul x=0 functia este continua.
Definiție. O funcție care este continuă pe un interval, cu excepția unui număr finit de discontinuități de primul fel sau a unei discontinuități amovibile, se spune că este continuă pe bucăți pe acest interval.

Exemple de funcții discontinue

Exemplul 4 Este posibil să se elimine întreruperile în funcții:
A) în punctul x=2;
b) în punctul x=2;
V) în punctul x=1?
Soluţie. Despre exemplul a), putem spune imediat că discontinuitatea f(x) în punctul x=2 nu poate fi eliminată, deoarece există infinite limite unilaterale în acest punct (vezi exemplul 1).
b) Funcția g(x) deși are limite unilaterale finite în punctul x=2

(,),

Exemplul numărul 5. Arătați că funcția Dirichlet

discontinuă în fiecare punct al axei numerice.
Soluţie. Fie x 0 orice punct din (-∞,+∞). În oricare dintre cartierele sale, există atât puncte raționale, cât și iraționale. Aceasta înseamnă că în orice vecinătate x 0 funcția va avea valori egale cu 0 și 1. În acest caz, nu poate exista o limită a funcției în punctul x 0 nici în stânga, nici în dreapta, ceea ce înseamnă că funcția Dirichlet în fiecare punct al axei reale are discontinuități de al doilea fel.

Exemplul 6 Găsiți punctele de întrerupere a funcției

Pentru o decizie independentă.
Investigați funcțiile pentru continuitate și determinați tipul punctelor de discontinuitate:
1) ; Răspuns: x=-1 – punctul de rupere;
2) ; Răspuns: Discontinuitate de al doilea fel în punctul x=8;
3) ; Raspuns: Discontinuitate de primul fel la x=1;
4)
Răspuns: În punctul x 1 \u003d -5 există un decalaj detașabil, la x 2 \u003d 1 - un decalaj de al doilea fel și în punctul x 3 \u003d 0 - un decalaj de primul fel.
5) Cum ar trebui să fie ales numărul A astfel încât funcția

ar fi continuu in punctul x=0?
Răspuns: A=2.
6) Este posibil să alegeți numărul A astfel încât funcția

ar fi continuu in punctul x=2?
Răspuns: nu.

Studiul funcției de continuitate într-un punct se realizează conform schemei de rutină deja rulată, care constă în verificarea a trei condiții de continuitate:

Exemplul 1

Investigați funcția pentru continuitate. Determinați natura întreruperilor de funcție, dacă există. Executați desenul.

Soluţie:

1) Singurul punct cade sub vedere, unde funcția nu este definită.

Limitele unilaterale sunt finite și egale.

Astfel, la un moment dat, funcția suferă o discontinuitate discontinuabilă.

Cum arată graficul acestei funcții?

vreau sa simplific , și pare a fi o parabolă obișnuită. DAR funcția originală nu este definită la punctul , așa că este necesară următoarea avertizare:

Să executăm desenul:

Răspuns: functia este continua pe toata dreapta numerica cu exceptia punctului in care sufera o discontinuitate.

Funcția poate fi redefinită într-un mod bun sau nu atât de bun, dar acest lucru nu este cerut de condiție.

Spui că exemplul este exagerat? Deloc. S-a întâmplat de zeci de ori în practică. Aproape toate sarcinile site-ului provin din muncă reală independentă și de control.

Să defalcăm modulele noastre preferate:

Exemplul 2

Funcția de explorare pentru continuitate. Determinați natura întreruperilor de funcție, dacă există. Executați desenul.

Soluţie: din anumite motive, elevilor le este frică și nu le plac funcțiile cu un modul, deși nu este nimic complicat la ele. Am atins deja puțin despre astfel de lucruri în lecție. Transformări ale diagramei geometrice. Deoarece modulul este nenegativ, se extinde în felul următor: , unde „alfa” este o expresie. În acest caz, și funcția noastră ar trebui să semneze pe bucăți:

Dar fracțiile ambelor piese trebuie reduse cu . Reducerea, ca în exemplul precedent, nu va fi fără consecințe. Funcția originală nu este definită la punctul, deoarece numitorul dispare. Prin urmare, sistemul ar trebui să specifice în plus condiția și să facă prima inegalitate strictă:

Acum pentru un truc FOARTE UTIL: înainte de a finaliza sarcina pe o schiță, este benefic să se realizeze un desen (indiferent dacă este cerut de condiție sau nu). Acest lucru vă va ajuta, în primul rând, să vedeți imediat punctele de continuitate și punctele de întrerupere și, în al doilea rând, vă va scuti 100% de erori atunci când găsiți limite unilaterale.

Hai să facem trucul. În conformitate cu calculele noastre, în stânga punctului este necesar să desenați un fragment de parabolă (albastru), iar la dreapta - o bucată de parabolă (roșu), în timp ce funcția nu este definită în punctul însuși. :

Când aveți îndoieli, luați câteva valori „x”, înlocuiți-le în funcție (amintindu-ne ca modulul distruge un posibil semn minus) si verificati graficul.

Investigăm funcția pentru continuitate analitic:

1) Funcția nu este definită la punctul , așa că putem spune imediat că nu este continuă la ea.

2) Să stabilim natura discontinuității, pentru aceasta calculăm limite unilaterale:

Limitele unilaterale sunt finite și diferite, ceea ce înseamnă că funcția suferă o discontinuitate de primul fel cu un salt în punctul . Rețineți că nu contează dacă funcția de la punctul de întrerupere este definită sau nu.

Acum rămâne să transferați desenul din schiță (a fost făcut, așa cum ar fi, cu ajutorul cercetării ;-)) și să finalizați sarcina:

Răspuns: functia este continua pe toata dreapta numerica cu exceptia punctului in care sufera o discontinuitate de primul fel cu un salt.

Uneori este necesară indicarea suplimentară a saltului de discontinuitate. Se calculează elementar - limita din stânga trebuie scăzută din limita dreaptă: , adică la punctul de rupere, funcția noastră a sărit cu 2 unități în jos (despre care ne spune semnul minus).

Exemplul 3

Funcția de explorare pentru continuitate. Determinați natura întreruperilor de funcție, dacă există. Faceți un desen.

Acesta este un exemplu pentru o soluție de tip do-it-yourself, eșantion exemplar soluții la sfârșitul lecției.

Să trecem la cea mai populară și comună versiune a sarcinii, când funcția constă din trei piese:

Exemplul 4

Investigați funcția pentru continuitate și trasați graficul funcției

.

Soluţie: este evident că toate cele trei părți ale funcției sunt continue pe intervalele corespunzătoare, așa că rămâne de verificat doar două puncte de „joncțiune” între piese. Mai întâi, să facem un desen pe o schiță, am comentat tehnica de construcție suficient de detaliat în prima parte a articolului. Singurul lucru este să urmărim cu atenție punctele noastre singulare: din cauza inegalității, valoarea aparține liniei drepte (punct verde), iar din cauza inegalității, valoarea aparține parabolei (punct roșu):


Ei bine, în principiu, totul este clar =) Rămâne de întocmit o decizie. Pentru fiecare dintre cele două puncte „cap la cap”, verificăm 3 condiții de continuitate ca standard:

eu)

1)

Limitele unilaterale sunt finite și diferite, ceea ce înseamnă că funcția suferă o discontinuitate de primul fel cu un salt în punctul .

Să calculăm saltul de discontinuitate ca diferență între limitele din dreapta și din stânga:
, adică graficul a sărit cu o unitate în sus.

II) Examinăm punctul de continuitate

1) - funcția este definită la punctul dat.

2) Găsiți limite unilaterale:

- limitele unilaterale sunt finite și egale, deci există o limită comună.

3)

În etapa finală, transferăm desenul într-o copie curată, după care punem acordul final:

Răspuns: functia este continua pe toata dreapta numerica, cu exceptia punctului in care sufera o discontinuitate de primul fel cu un salt.

Exemplul 5

Investigați o funcție pentru continuitate și construiți graficul acesteia .

Acesta este un exemplu pentru o soluție independentă, o soluție scurtă și un eșantion aproximativ al problemei la sfârșitul lecției.

Se poate avea impresia că la un moment dat funcția trebuie să fie neapărat continuă, iar la un alt punct trebuie neapărat să existe o discontinuitate. În practică, acest lucru nu este întotdeauna cazul. Încercați să nu neglijați exemplele rămase - vor exista câteva caracteristici interesante și importante:

Exemplul 6

Dată o funcție . Investigați funcția pentru continuitate în puncte. Construiți un grafic.

Soluţie: și din nou executați imediat desenul pe proiect:

Particularitatea acestui grafic este că pentru funcția pe bucăți este dată de ecuația axei absciselor. Această zonă este afișată aici în verde, iar într-un caiet este de obicei evidențiat cu aldine cu un simplu creion. Și, bineînțeles, nu uitați de oile noastre: valoarea se referă la ramura tangentă (punct roșu), iar valoarea aparține liniei drepte.

Totul este clar din desen - funcția este continuă pe întreaga linie numerică, rămâne să elaborăm o soluție care este adusă la un automatism complet după 3-4 exemple similare:

eu) Examinăm punctul de continuitate

2) Calculați limitele unilaterale:

, deci există o limită comună.

A fost o mică întorsătură aici. Cert este că am creat o mulțime de materiale despre limitele funcției, și de câteva ori am vrut, dar de câteva ori am uitat de o întrebare simplă. Și așa, cu un efort de voință incredibil, m-am forțat să nu-mi pierd gândul =) Cel mai probabil, unii cititori-„maniști” se îndoiesc: care este limita constantei? Limita unei constante este egală cu constanta însăși. În acest caz, limita lui zero este egală cu zero în sine (limita din stânga).

3) - limita unei funcţii într-un punct este egală cu valoarea acestei funcţii într-un punct dat.

Astfel, o funcție este continuă într-un punct prin definiția unei funcții fiind continuă într-un punct.

II) Examinăm punctul de continuitate

1) - funcția este definită la un punct dat.

2) Găsiți limite unilaterale:

Și aici, în limita din dreapta - limita unității este egală cu unitatea în sine.

- există o limită generală.

3) - limita unei funcţii într-un punct este egală cu valoarea acestei funcţii într-un punct dat.

Astfel, o funcție este continuă într-un punct prin definiția unei funcții fiind continuă într-un punct.

Ca de obicei, după studiu, ne transferăm desenul într-o copie curată.

Răspuns: functia este continua in puncte .

Vă rugăm să rețineți că în condiția nu am fost întrebați nimic despre studiul întregii funcții pentru continuitate și este considerată o formă matematică bună de a formula precisă și clară răspuns la întrebarea pusă. Apropo, dacă în funcție de condiție nu este necesar să construiți un grafic, atunci aveți tot dreptul să nu îl construiți (deși mai târziu profesorul vă poate obliga să faceți acest lucru).

Un mic "șochet" matematic pentru o soluție independentă:

Exemplul 7

Dată o funcție .

Investigați funcția pentru continuitate în puncte. Clasificați punctele de întrerupere, dacă există. Executați desenul.

Încercați să „pronunțați” corect toate „cuvintele” =) Și desenați graficul mai precis, acuratețe, nu va fi de prisos peste tot ;-)

După cum vă amintiți, ți-am recomandat să desenați imediat pe o schiță, dar din când în când există astfel de exemple în care nu vă puteți da seama imediat cum arată graficul. Prin urmare, într-o serie de cazuri, este avantajos să găsim mai întâi limite unilaterale și abia apoi, pe baza studiului, să descriem ramurile. În ultimele două exemple, vom învăța și tehnica calculării unor limite unilaterale:

Exemplul 8

Investigați o funcție pentru continuitate și construiți graficul ei schematic.

Soluţie: punctele proaste sunt evidente: (face numitorul exponentului la zero) și (reduce la zero numitorul întregii fracții). Nu este clar cum arată graficul acestei funcții, ceea ce înseamnă că este mai bine să efectuați mai întâi un studiu:

eu) Examinăm punctul de continuitate

2) Găsiți limite unilaterale:

fi atent la o metodă tipică pentru calcularea unei limite unilaterale: în funcție în loc de „X” înlocuim . Nu există nicio crimă în numitor: „adăugarea” „minus zero” nu joacă un rol și rezultă „patru”. Dar în numărător există un mic thriller: mai întâi, omorâm -1 și 1 în numitorul indicatorului, în urma căruia obținem . unitate împărțită la , este egal cu „minus infinit”, prin urmare: . Și în sfârșit, cei „doi” în infinit de mare grad negativ egal cu zero: . Sau, mai detaliat: .

Să calculăm limita din dreapta:

Și aici - în loc de „x” înlocuim . La numitor, „aditiv” din nou nu joacă un rol: . În numărător, se efectuează acțiuni similare cu limita anterioară: distrugem numerele opuse și împărțim unitatea la :

Limita din dreapta este infinită, ceea ce înseamnă că funcția suferă o discontinuitate de al 2-lea fel în punctul .

II) Examinăm punctul de continuitate

1) Funcția nu este definită în acest moment.

2) Calculați limita din stânga:

Metoda este aceeași: înlocuim în funcție în loc de „x”. Nu există nimic interesant în numărător - se dovedește un număr pozitiv finit. Și în numitor deschidem parantezele, eliminăm „triplele”, iar „aditivul” joacă un rol decisiv.

Drept urmare, final număr pozitiv impartit de număr pozitiv infinitezimal, dă „plus infinit”: .

Limita dreaptă, ca un frate geamăn, cu singura excepție care apare la numitor număr negativ infinitezimal:

Limitele unilaterale sunt infinite, ceea ce înseamnă că funcția suferă o discontinuitate de al 2-lea fel în punctul .

Astfel, avem două puncte de întrerupere și, evident, trei ramuri ale graficului. Pentru fiecare ramură, este indicat să se realizeze o construcție punct cu punct, adică. luați mai multe valori ale lui "x" și înlocuiți-le în . Rețineți că condiția permite construirea unui desen schematic, iar o astfel de relaxare este naturală pentru munca manuală. Construiesc grafice folosind un program, așa că nu am astfel de dificultăți, iată o imagine destul de precisă:

Sunt directe asimptote verticale pentru graficul acestei funcții.

Răspuns: functia este continua pe toata dreapta numerica, cu exceptia punctelor in care sufera discontinuitati de al 2-lea fel.

O funcție mai simplă pentru o soluție do-it-yourself:

Exemplul 9

Investigați funcția pentru continuitate și faceți un desen schematic.

O soluție de probă la sfârșit care s-a strecurat neobservată.

Pe curând!

Solutii si raspunsuri:

Exemplul 3:Soluţie : transforma functia: . Având în vedere regula de extindere a modulului si faptul ca , rescriem funcția sub formă de bucăți:


Investigăm funcția pentru continuitate.

1) Funcția nu este definită la punctul .

Limitele unilaterale sunt finite și diferite, ceea ce înseamnă că funcția suferă o discontinuitate de primul fel cu un salt la punct . Să executăm desenul:

Răspuns: funcția este continuă pe întreaga linie numerică, cu excepția punctului , în care suferă o discontinuitate de primul fel cu un salt. Salt de gol: (două unități în sus).

Exemplul 5:Soluţie : fiecare dintre cele trei părți ale funcției este continuă pe intervalul său.
eu)
1)

2) Calculați limitele unilaterale:

, deci există o limită comună.
3) - limita unei funcţii într-un punct este egală cu valoarea acestei funcţii într-un punct dat.
Deci funcția continuu la un punct prin definiţia continuităţii unei funcţii într-un punct.
II) Examinăm punctul de continuitate

1) - funcția este definită la punctul dat. functia sufera o discontinuitate de al 2-lea fel, la punct

Cum să găsiți domeniul de aplicare al unei funcții?

Exemple de soluții

Dacă ceva lipsește undeva, atunci există ceva undeva

Continuăm să studiem secțiunea „Funcții și grafice”, iar următoarea stație a călătoriei noastre este Domeniul de aplicare a funcției. O discuție activă a acestui concept a început chiar din prima lecție. despre graficele de funcții, unde m-am uitat la funcțiile elementare și, în special, domeniul lor. Prin urmare, recomand ca manechinele să înceapă cu elementele de bază ale subiectului, deoarece nu mă voi opri din nou asupra unora dintre punctele de bază.

Se presupune că cititorul cunoaște zonele de definire a principalelor funcții: funcții liniare, pătratice, cubice, polinoame, exponent, logaritm, sinus, cosinus. Ele sunt definite pe . Pentru tangente, arcsinus, așa să fie, vă iert =) Graficele mai rare nu sunt amintite imediat.

Domeniul definiției pare a fi un lucru simplu și apare o întrebare firească, despre ce va fi articolul? Pe această lecție Voi lua în considerare sarcini comune pentru găsirea domeniului de aplicare a unei funcții. În plus, vom repeta inegalități cu o variabilă, abilitățile de rezolvat care vor fi necesare în alte sarcini matematică superioară. Materialul, apropo, este tot școlar, așa că va fi util nu numai elevilor, ci și elevilor. Informația, desigur, nu se pretinde a fi enciclopedică, dar, pe de altă parte, nu există aici exemple exagerate de „morți”, ci castane prăjite, care sunt preluate din adevărate lucrări practice.

Să începem cu o tăietură expresă a subiectului. Pe scurt despre principalul lucru: vorbim despre o funcție a unei variabile. Domeniul său de definire este set de valori „x”., pentru care exista sensul de „jocuri”. Luați în considerare un exemplu ipotetic:

Domeniul acestei funcții este uniunea intervalelor:
(pentru cei care au uitat: - pictograma îmbinare). Cu alte cuvinte, dacă luăm orice valoare a lui "x" din intervalul , sau din , sau din , atunci pentru fiecare astfel de "x" va exista o valoare a lui "y".

În linii mari, acolo unde este domeniul definiției, există un grafic al funcției. Dar semi-intervalul și punctul „ce” nu sunt incluse în zona de definiție, așa că nu există nici un grafic acolo.

Apropo, dacă ceva nu este clar din terminologia și/sau conținutul primelor paragrafe, este mai bine să reveniți la articol Grafice și proprietăți ale funcțiilor elementare.

Definiția lui Heine a continuității

Se spune că funcția unei variabile reale \(f\left(x \right)\) este continuu în punctul \(a \in \mathbb(R)\) (\(\mathbb(R)-\)set numere reale) dacă pentru orice secvență \(\left\( ((x_n)) \right\)\) astfel încât \[\lim\limits_(n \to \infty ) (x_n) = a,\] relația \[\ lim\limits_(n \to \infty ) f\left(((x_n)) \right) = f\left(a \right).\] În practică, este convenabil să folosiți următoarea continuitate \(3\) condiții pentru o funcție \(f\left(x \right)\) în punctul \(x = a\) (care trebuie să ruleze simultan):

1. Funcția \(f\left(x \right)\) este definită în punctul \(x = a\);
2. Limita \(\lim\limits_(x \to a) f\left(x \right)\) există;
3. Egalitatea \(\lim\limits_(x \to a) f\left(x \right) = f\left(a \right)\) este satisfăcută.

Definiția continuității Cauchy (notația \(\varepsilon - \delta\))

Luați în considerare funcția \(f\left(x \right)\), care mapează mulțimea de numere reale \(\mathbb(R)\) pe o altă submulțime \(B\) de numere reale. Se spune că funcția \(f\left(x \right)\) este continuu în punctul \(a \in \mathbb(R)\) dacă pentru orice număr \(\varepsilon > 0\) există un număr \(\delta > 0\) astfel încât pentru toate \(x \in \mathbb (R)\) satisfacând relația \[\left| (x - a) \dreapta| Definirea continuității în termeni de incremente de argument și funcție

Definiția continuității poate fi formulată și folosind incremente de argument și funcție. Funcția este continuă în punctul \(x = a\) dacă \[\lim\limits_(\Delta x \to 0) \Delta y = \lim\limits_(\Delta x \to 0) \left[ ( f \left((a + \Delta x) \right) - f\left(a \right)) \right] = 0,\] unde \(\Delta x = x - a\).

Definițiile de mai sus ale continuității unei funcții sunt echivalente pe mulțimea numerelor reale.

Funcția este continuu pe acest interval dacă este continuă în fiecare punct al acestui interval.

Teoreme de continuitate

Teorema 2.
Dat fiind două funcții \((f\left(x \right))\) și \((g\left(x \right))\) continue în punctul \(x = a\). Apoi, suma acestor funcții \((f\left(x \right)) + (g\left(x \right))\) este, de asemenea, continuă în punctul \(x = a\).

Teorema 3.
Să presupunem că două funcții \((f\left(x \right))\) și \((g\left(x \right))\) sunt continue în punctul \(x = a\). Apoi produsul acestor funcții \((f\left(x \right)) (g\left(x \right))\) este de asemenea continuu în punctul \(x = a\).

Teorema 4.
Date fiind două funcții \((f\left(x \right))\) și \((g\left(x \right))\) care sunt continue pentru \(x = a\). Atunci raportul acestor funcții \(\large\frac((f\left(x \right)))((g\left(x \right)))\normalsize\) este, de asemenea, continuu pentru \(x = a\ ) cu condiția ca \((g\left(a \right)) \ne 0\).

Teorema 5.
Să presupunem că funcția \((f\left(x \right))\) este diferențiabilă în punctul \(x = a\). Atunci funcția \((f\left(x \right))\) este continuă în acest punct (adică din diferențiere rezultă că funcția este continuă în punct; inversul nu este adevărat).

Teorema 6 (Teorema valorii limită).
Dacă o funcție \((f\left(x \right))\) este continuă pe un interval închis și mărginit \(\left[ (a,b) \right]\), atunci este mărginită deasupra și dedesubt pe interval dat. Cu alte cuvinte, există numere \(m\) și \(M\) astfel încât \ pentru toate \(x\) din intervalul \(\left[ (a,b) \right]\) (Figura 1) .

Continuitatea funcțiilor elementare

Toate functii elementare sunt continue în orice punct al domeniului lor de definire.

Funcția este numită elementar , dacă este construit dintr-un număr finit de compoziții și combinații
(folosind operații \(4\) - adunare, scădere, înmulțire și împărțire) . O multime de funcții elementare de bază include:

În această lecție, vom învăța cum să stabilim continuitatea unei funcții. Vom face acest lucru cu ajutorul limitelor, în plus, unilaterale - dreapta și stânga, care nu sunt deloc înfricoșătoare, în ciuda faptului că sunt scrise ca și .

Dar care este continuitatea unei funcții în general? Până ajungem la o definiție strictă, cel mai simplu mod de a ne imagina o linie care poate fi trasă fără a ridica creionul de pe hârtie. Dacă o astfel de linie este trasată, atunci este continuă. Această linie este graficul unei funcții continue.

Grafic, o funcție este continuă într-un punct dacă graficul ei nu se „rupe” în acel punct. Graficul unei astfel de funcții continue este prezentat în figura de mai jos.

Definirea continuitatii unei functii prin limita. O funcție este continuă într-un punct în trei condiții:

1. Funcția este definită la punctul .

Dacă cel puțin una dintre condițiile de mai sus nu este îndeplinită, funcția nu este continuă într-un punct. În același timp, ei spun că funcția suferă o întrerupere, iar punctele de pe grafic la care graficul este întrerupt se numesc puncte de întrerupere ale funcției. Graficul unei astfel de funcții, care suferă o întrerupere în punctul x=2, este prezentat în figura de mai jos.

Exemplul 1 Funcţie f(X) este definită după cum urmează:

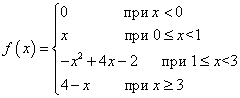
Va fi această funcție continuă în fiecare dintre punctele de graniță ale ramurilor sale, adică în puncte? X = 0 , X = 1 , X = 3 ?

Soluţie. Verificăm toate cele trei condiții pentru continuitatea funcției în fiecare punct de limită. Prima condiție este îndeplinită deoarece functie definita la fiecare dintre punctele limită rezultă din definiţia funcţiei. Rămâne de verificat celelalte două condiții.

Punct X= 0 . Găsiți limita din stânga în acest punct:

.

Să găsim limita din dreapta:

X= 0 trebuie găsit la ramura funcției care include acest punct, adică a doua ramură. Le gasim:

După cum puteți vedea, limita funcției și valoarea funcției la punctul X= 0 sunt egale. Prin urmare, funcția este continuă în punct X = 0 .

Punct X= 1 . Găsiți limita din stânga în acest punct:

Să găsim limita din dreapta:

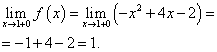
Limita funcției și valoarea funcției la un punct X= 1 trebuie găsit la ramura funcției care include acest punct, adică a doua ramură. Le gasim:

.

Limita funcției și valoarea funcției la un punct X= 1 sunt egale. Prin urmare, funcția este continuă în punct X = 1 .

Punct X= 3 . Găsiți limita din stânga în acest punct:

Să găsim limita din dreapta:

Limita funcției și valoarea funcției la un punct X= 3 trebuie găsit la ramura funcției care include acest punct, adică a doua ramură. Le gasim:

.

Limita funcției și valoarea funcției la un punct X= 3 sunt egale. Prin urmare, funcția este continuă în punct X = 3 .

Concluzia principală: această funcție este continuă în fiecare punct de limită.

Ce este schimbarea continuă a funcției?

O modificare continuă a unei funcții poate fi definită ca o schimbare treptată, fără salturi, în care o mică modificare a argumentului implică o mică schimbare a funcției.

Să ilustrăm această schimbare continuă a funcției cu un exemplu.

Lasă o încărcătură să atârne de un fir deasupra mesei. Sub acțiunea acestei sarcini, firul este întins, deci distanța l sarcina din punctul de suspendare a filetului este o funcție de masa sarcinii m, acesta este l = f(m) , m≥0 .

Dacă modificăm ușor masa încărcăturii, atunci distanța l little change: mica schimbare m corespund micilor modificări l. Cu toate acestea, dacă masa încărcăturii este apropiată de rezistența la tracțiune a firului, atunci o mică creștere a masei încărcăturii poate provoca ruperea firului: distanța l va crește brusc și va deveni egală cu distanța de la punctul de suspendare la suprafața mesei. Graficul funcției l = f(m) prezentată în figură. Pe site, acest grafic este o linie continuă (solidă), iar în punctul acesta este întrerupt. Rezultatul este un grafic format din două ramuri. În toate punctele, cu excepția funcției l = f(m) este continuu, iar la un moment dat are o discontinuitate.

Studiul unei funcții pentru continuitate poate fi atât o sarcină independentă, cât și una dintre etapele unui studiu complet al funcției și construcția graficului acesteia.

Continuitatea unei funcții pe un interval

Lasă funcția y = f(X) definit în intervalul ] A, b[ și este continuă în fiecare punct al acestui interval. Apoi se numește continuu în intervalul ] A, b[ . Conceptul de continuitate a unei funcții pe intervale de forma ]- ∞ este definit în mod similar, b[ , ]A, + ∞[ , ]- ∞, + ∞[ . Acum lăsați funcția y = f(X) definit pe intervalul [ A, b] . Diferența dintre un interval și un segment este că punctele limită ale intervalului nu sunt incluse în interval, dar punctele limită ale segmentului sunt incluse în segment. Aici ar trebui să amintim așa-numita continuitate unilaterală: la punct A, rămânând pe intervalul [ A, b] , ne putem apropia doar din dreapta, și la obiect b- doar in stanga. Funcția se numește continuă pe segmentul [ A, b] , dacă este continuă în toate punctele interioare ale acestui segment, continuă în dreapta în punctul respectiv Ași lăsat continuu la punct b.

Oricare dintre funcțiile elementare poate servi ca exemplu de funcție continuă. Fiecare funcție elementară este continuă pe orice segment pe care este definită. De exemplu, funcțiile și sunt continue pe orice interval [ A, b] , funcția este continuă pe intervalul [ 0 , b] , funcția este continuă pe orice segment care nu conține un punct A = 2 .

Exemplul 4 Investigați funcția pentru continuitate.

Soluţie. Să verificăm prima condiție. Funcția nu este definită la punctele - 3 și 3. Cel puțin una dintre condițiile pentru continuitatea funcției pe întreaga linie numerică nu este îndeplinită. Prin urmare, această funcție este continuă pe intervale

Exemplul 5 Determinați la ce valoare a parametrului A continuă pe tot parcursul domenii funcţie

Soluţie.

Să găsim limita din dreapta pentru:

.

Este evident că valoarea la punct X= 2 trebuie să fie egal topor :

A = 1,5 .

Exemplul 6 Determinați la ce valori ale parametrilor AȘi b continuă pe tot parcursul domenii funcţie

Soluţie.
Găsiți limita din stânga a funcției în punctul:

.

Prin urmare, valoarea punctului trebuie să fie egală cu 1:

Să găsim funcția din partea stângă la punctul:

În mod evident, valoarea funcției în punct ar trebui să fie egală cu:

Răspuns: funcția este continuă pe întregul domeniu de definire pentru A = 1; b = -3 .

Proprietățile de bază ale funcțiilor continue

Matematica a ajuns la conceptul de funcție continuă studiind, în primul rând, diferitele legi ale mișcării. Spațiul și timpul sunt nesfârșite și dependența ca căile s din timp t, exprimate prin lege s = f(t) , oferă un exemplu de continuu funcții f(t) . Temperatura apei încălzite se modifică și ea continuu, este și o funcție continuă a timpului: T = f(t) .

ÎN analiză matematică sunt dovedite unele proprietăţi deţinute de funcţiile continue. Vă prezentăm cele mai importante dintre aceste proprietăți.

1. Dacă o funcție care este continuă pe un interval ia valori de diferite semne la sfârșitul intervalului, atunci la un punct al acestui segment ia o valoare egală cu zero. Mai formal, această proprietate este dată într-o teoremă cunoscută sub numele de prima teoremă Bolzano-Cauchy.

2. Funcția f(X), continuu pe intervalul [ A, b] , ia toate valorile intermediare dintre valorile de la punctele finale, adică între f(A) Și f(b) . Mai formal, această proprietate este dată într-o teoremă cunoscută sub numele de a doua teoremă Bolzano-Cauchy.