Metode probabilistic-statistice de cercetare și metoda analizei de sistem. Metode statistice Analiza statistică a datelor specifice

3. Esenţa metodelor probabilistic-statistice

Cum sunt utilizate abordările, ideile și rezultatele teoriei probabilităților și statisticii matematice la prelucrarea datelor - rezultatele observațiilor, măsurătorilor, testelor, analizelor, experimentelor pentru a lua decizii practic importante?

Baza este un model probabilistic al unui fenomen sau proces real, i.e. un model matematic în care relaţiile obiective sunt exprimate în termeni de teoria probabilităţilor. Probabilitățile sunt folosite în primul rând pentru a descrie incertitudinile care trebuie luate în considerare la luarea deciziilor. Aceasta se referă atât la oportunități nedorite (riscuri), cât și la cele atractive („șansa norocoasă”). Uneori, aleatorietatea este introdusă în mod deliberat într-o situație, de exemplu, la tragere la sorți, la selectarea aleatorie a unităților pentru control, la desfășurarea loteriei sau la efectuarea de sondaje ale consumatorilor.

Teoria probabilității permite utilizarea unei probabilități pentru a calcula altele de interes pentru cercetător. De exemplu, folosind probabilitatea de a obține o stemă, puteți calcula probabilitatea ca în 10 aruncări de monede să obțineți cel puțin 3 steme. Un astfel de calcul se bazează pe un model probabilistic, conform căruia aruncările de monede sunt descrise printr-un model de încercări independente; în plus, stema și semnele hash sunt la fel de posibile și, prin urmare, probabilitatea fiecăruia dintre aceste evenimente este egală. la ½. Un model mai complex este cel care are în vedere verificarea calității unei unități de producție în loc să arunce o monedă. Modelul probabilistic corespunzător se bazează pe presupunerea că controlul calității diferitelor unități de producție este descris printr-o schemă de testare independentă. Spre deosebire de modelul de aruncare a monedelor, este necesar să se introducă un nou parametru - probabilitatea R că produsul este defect. Modelul va fi pe deplin descris dacă presupunem că toate unitățile de producție au aceeași probabilitate de a fi defecte. Dacă ultima ipoteză este incorectă, atunci numărul parametrilor modelului crește. De exemplu, puteți presupune că fiecare unitate de producție are propria probabilitate de a fi defectă.

Să discutăm despre un model de control al calității cu o probabilitate de defectivitate comună tuturor unităților de producție R. Pentru a „a ajunge la număr” atunci când se analizează modelul, este necesar să se înlocuiască R la o anumită valoare. Pentru a face acest lucru, este necesar să trecem dincolo de modelul probabilistic și să apelăm la datele obținute în timpul controlului calității. Statistica matematică rezolvă problema inversă în raport cu teoria probabilității. Scopul său este, pe baza rezultatelor observațiilor (măsurători, analize, teste, experimente), de a obține concluzii despre probabilitățile care stau la baza modelului probabilistic. De exemplu, pe baza frecvenței de apariție a produselor defecte în timpul inspecției, se pot trage concluzii despre probabilitatea defectiunii (vezi discuția de mai sus folosind teorema lui Bernoulli). Pe baza inegalității lui Chebyshev, s-au tras concluzii cu privire la corespondența frecvenței de apariție a produselor defecte cu ipoteza că probabilitatea defectiunii ia o anumită valoare.

Astfel, aplicarea statisticii matematice se bazează pe un model probabilistic al unui fenomen sau proces. Sunt utilizate două serii paralele de concepte - cele legate de teorie (model probabilistic) și cele legate de practică (eșantionarea rezultatelor observației). De exemplu, probabilitatea teoretică corespunde frecvenței găsite din eșantion. Aşteptările matematice (seria teoretică) corespunde mediei aritmetice eşantionului (seria practică). De regulă, caracteristicile eșantionului sunt estimări ale celor teoretice. În același timp, cantitățile legate de seria teoretică „sunt în capul cercetătorilor”, se referă la lumea ideilor (conform filosofului grec antic Platon) și nu sunt disponibile pentru măsurare directă. Cercetătorii au doar date eșantion cu care încearcă să stabilească proprietățile unui model probabilistic teoretic care îi interesează.

De ce avem nevoie de un model probabilistic? Cert este că numai cu ajutorul lui proprietățile stabilite din analiza unui eșantion anume pot fi transferate altor probe, precum și întregii așa-zise populații generale. Termenul „populație” este folosit atunci când se referă la o colecție mare, dar finită de unități studiate. De exemplu, despre totalitatea tuturor rezidenților Rusiei sau totalitatea tuturor consumatorilor de cafea instant din Moscova. Scopul anchetelor de marketing sau sociologice este de a transfera afirmațiile obținute dintr-un eșantion de sute sau mii de oameni către populații de câteva milioane de oameni. În controlul calității, un lot de produse acționează ca o populație generală.

Pentru a transfera concluziile de la un eșantion la o populație mai mare necesită unele ipoteze despre relația dintre caracteristicile eșantionului cu caracteristicile acestei populații mai mari. Aceste ipoteze se bazează pe un model probabilistic adecvat.

Desigur, este posibil să se prelucreze date eșantionului fără a utiliza unul sau altul model probabilistic. De exemplu, puteți calcula o medie aritmetică eșantion, puteți număra frecvența de îndeplinire a anumitor condiții etc. Cu toate acestea, rezultatele calculului se vor referi doar la un eșantion specific; transferul concluziilor obținute cu ajutorul lor către orice altă populație este incorect. Această activitate este uneori numită „analiza datelor”. Comparativ cu metodele probabilistic-statistice, analiza datelor are valoare educațională limitată.

Deci, utilizarea modelelor probabilistice bazate pe estimarea și testarea ipotezelor folosind caracteristicile eșantionului este esența metodelor probabilistic-statistice de luare a deciziilor.

Subliniem că logica utilizării caracteristicilor eșantionului pentru luarea deciziilor bazate pe modele teoretice presupune utilizarea simultană a două serii paralele de concepte, dintre care una corespunde modelelor probabilistice, iar a doua eșantionării datelor. Din păcate, într-o serie de surse literare, de obicei învechite sau scrise în spirit de rețetă, nu se face distincție între eșantion și caracteristicile teoretice, ceea ce duce cititorii la confuzii și erori în utilizarea practică a metodelor statistice.

În conformitate cu cele trei posibilități principale - luarea deciziilor în condiții de certitudine completă, risc și incertitudine - metodele și algoritmii de luare a deciziilor pot fi împărțiți în trei tipuri principale: analitice, statistice și bazate pe formalizare fuzzy. În fiecare caz specific, metoda de luare a deciziilor este selectată pe baza sarcinii în cauză, a datelor sursă disponibile, a modelelor de probleme disponibile, a mediului decizional, a procesului de luare a deciziilor, a acurateței necesare deciziei și a preferințelor personale ale analistului.

În unele sisteme informatice, procesul de selectare a unui algoritm poate fi automatizat:

Sistemul automatizat corespunzător are capacitatea de a utiliza multe tipuri diferite de algoritmi (biblioteca de algoritmi);

Sistemul solicită în mod interactiv utilizatorul să răspundă la o serie de întrebări despre principalele caracteristici ale sarcinii luate în considerare;

Pe baza rezultatelor răspunsurilor utilizatorului, sistemul oferă cel mai potrivit (în conformitate cu criteriile specificate în acesta) algoritm din bibliotecă.

2.3.1 Metode probabilistice și statistice de luare a deciziilor

Metodele probabilistic-statistice de luare a deciziilor (PSD) sunt utilizate în cazul în care eficacitatea deciziilor luate depinde de factori care sunt variabile aleatorii pentru care sunt cunoscute legile distribuției probabilităților și alte caracteristici statistice. Mai mult, fiecare decizie poate duce la unul dintre multele rezultate posibile, iar fiecare rezultat are o anumită probabilitate de apariție, care poate fi calculată. Indicatorii care caracterizează o situație problemă sunt descriși și folosind caracteristici probabilistice.Cu un astfel de ZPR, decidentul riscă întotdeauna să obțină un rezultat care nu este cel către care se orientează atunci când alege soluția optimă pe baza caracteristicilor statistice medii ale factorilor aleatori. , adică decizia se ia în condiții de risc.

În practică, metodele probabilistice și statistice sunt adesea utilizate atunci când concluziile extrase din datele eșantionului sunt transferate întregii populații (de exemplu, de la un eșantion la un întreg lot de produse). Cu toate acestea, în fiecare situație specifică, ar trebui mai întâi să se evalueze posibilitatea fundamentală de a obține date probabilistice și statistice suficient de fiabile.

Atunci când se folosesc ideile și rezultatele teoriei probabilităților și ale statisticii matematice la luarea deciziilor, baza este un model matematic în care relațiile obiective sunt exprimate în termeni de teoria probabilității. Probabilitățile sunt folosite în primul rând pentru a descrie aleatorietatea care trebuie luată în considerare la luarea deciziilor. Aceasta se referă atât la oportunități nedorite (riscuri), cât și la cele atractive („șansa norocoasă”).

Esența metodelor probabilistic-statistice de luare a deciziilor este utilizarea modelelor probabilistice bazate pe estimarea și testarea ipotezelor folosind caracteristicile eșantionului.

Subliniem că logica utilizării caracteristicilor eșantionului pentru a lua decizii bazate pe modele teoretice presupune utilizarea simultană a două serii paralele de concepte– legate de teorie (model probabilistic) și legate de practică (eșantionarea rezultatelor observației). De exemplu, probabilitatea teoretică corespunde frecvenței găsite din eșantion. Aşteptările matematice (seria teoretică) corespunde mediei aritmetice eşantionului (seria practică). De obicei, caracteristicile eșantionului sunt estimări ale caracteristicilor teoretice.

Avantajele utilizării acestor metode includ capacitatea de a lua în considerare diferite scenarii pentru desfășurarea evenimentelor și probabilitățile acestora. Dezavantajul acestor metode este că valorile probabilității pentru scenariile utilizate în calcule sunt de obicei foarte greu de obținut în practică.

Aplicarea unei metode decizionale probabilistic-statistice specifice constă în trei etape:

Trecerea de la realitatea economică, managerială, tehnologică la o schemă abstractă matematică și statistică, i.e. construirea unui model probabilistic al unui sistem de control, proces tehnologic, procedură de luare a deciziilor, în special pe baza rezultatelor controlului statistic etc.

Efectuarea de calcule și tragerea de concluzii folosind mijloace pur matematice în cadrul unui model probabilistic;

Interpretarea concluziilor matematice și statistice în raport cu o situație reală și luarea unei decizii adecvate (de exemplu, cu privire la conformitatea sau nerespectarea calității produsului cu cerințele stabilite, necesitatea ajustării procesului tehnologic etc.), în special, concluzii (cu privire la proporția de unități defecte de produs într-un lot, asupra formei specifice a legilor de distribuție a parametrilor controlați ai procesului tehnologic etc.).

Un model probabilistic al unui fenomen real ar trebui considerat construit dacă mărimile luate în considerare și conexiunile dintre ele sunt exprimate în termeni de teoria probabilității. Adecvarea modelului probabilistic este fundamentată, în special, folosind metode statistice de testare a ipotezelor.

Pe baza tipului de problemă rezolvată, statistica matematică este de obicei împărțită în trei secțiuni: descrierea datelor, estimarea și testarea ipotezelor. Pe baza tipului de date statistice prelucrate, statistica matematică este împărțită în patru domenii:

Statistica univariată (statistica variabilelor aleatoare), în care rezultatul unei observații este descris printr-un număr real;

Analiza statistică multivariată, în care rezultatul observării unui obiect este descris prin mai multe numere (vector);

Statistica proceselor aleatoare și a seriilor de timp, unde rezultatul observației este o funcție;

Statistica obiectelor de natură nenumerică, în care rezultatul unei observații este de natură nenumerică, de exemplu, este o mulțime (o figură geometrică), o ordonare sau obținută ca urmare a unei măsurători bazate pe un criteriu calitativ.

Un exemplu când se recomandă utilizarea modelelor probabilistic-statistice.

Atunci când se controlează calitatea oricărui produs, o probă este selectată din acesta pentru a decide dacă lotul de produse care se produce îndeplinește cerințele stabilite. Pe baza rezultatelor controlului probei, se face o concluzie despre întregul lot. În acest caz, este foarte important să se evite subiectivitatea atunci când se formează o probă, adică este necesar ca fiecare unitate de produs din lotul controlat să aibă aceeași probabilitate de a fi selectată pentru probă. Selecția pe bază de lot într-o astfel de situație nu este suficient de obiectivă. Prin urmare, în condiții de producție, selecția unităților de produs pentru eșantion se realizează de obicei nu prin lot, ci prin tabele speciale de numere aleatorii sau folosind senzori de numere aleatoare de calculator.

În reglementarea statistică a proceselor tehnologice, pe baza metodelor statisticii matematice, se elaborează reguli și planuri pentru controlul proceselor statistice, care vizează detectarea în timp util a problemelor din procesele tehnologice și luarea de măsuri pentru ajustarea acestora și prevenirea eliberării produselor care nu îndeplini cerințele stabilite. Aceste măsuri vizează reducerea costurilor de producție și a pierderilor din furnizarea de unități de calitate scăzută. În timpul controlului statistic de acceptare, pe baza metodelor statisticii matematice, se elaborează planuri de control al calității prin analiza probelor din loturile de produse. Dificultatea constă în a putea construi corect modele probabilistic-statistice de luare a deciziilor, pe baza cărora să se răspundă la întrebările puse mai sus. În statistica matematică au fost dezvoltate în acest scop modele probabilistice și metode de testare a ipotezelor3.

În plus, într-o serie de situații manageriale, de producție, economice și economice naționale, apar probleme de alt tip - probleme de evaluare a caracteristicilor și parametrilor distribuțiilor probabilităților.

Sau, atunci când se analizează statistic acuratețea și stabilitatea proceselor tehnologice, este necesar să se evalueze astfel de indicatori de calitate precum valoarea medie a parametrului controlat și gradul de împrăștiere a acestuia în procesul luat în considerare. Conform teoriei probabilităților, este recomandabil să se folosească așteptarea sa matematică ca valoare medie a unei variabile aleatoare și dispersia, abaterea standard sau coeficientul de variație ca caracteristică statistică a răspândirii. Aceasta ridică întrebarea: cum să estimați aceste caracteristici statistice din datele eșantionului și cu ce precizie se poate face acest lucru? Există multe exemple similare în literatură. Toate arată cum teoria probabilității și statistica matematică pot fi utilizate în managementul producției atunci când se iau decizii în domeniul managementului statistic al calității produselor.

În domenii specifice de aplicare se folosesc atât metode probabilistice, cât și statistice de aplicare generală, cât și cele specifice. De exemplu, în secțiunea de management al producției dedicată metodelor statistice de management al calității produselor, sunt utilizate statistici matematice aplicate (inclusiv proiectarea experimentelor). Folosind metodele sale, se realizează analiza statistică a acurateței și stabilității proceselor tehnologice și evaluarea statistică a calității. Metodele specifice includ metode de control statistic al acceptării calității produselor, reglementarea statistică a proceselor tehnologice, evaluarea și controlul fiabilității etc.

În managementul producției, în special, atunci când se optimizează calitatea produsului și se asigură respectarea cerințelor standard, este deosebit de important să se aplice metode statistice în etapa inițială a ciclului de viață al produsului, de exemplu. în stadiul cercetării pregătirea dezvoltărilor de proiectare experimentală (dezvoltarea cerințelor de produs promițătoare, proiectare preliminară, specificații tehnice pentru dezvoltarea designului experimental). Acest lucru se datorează informațiilor limitate disponibile în etapa inițială a ciclului de viață al produsului și necesității de a prezice capacitățile tehnice și situația economică pentru viitor.

Cele mai comune metode statistice probabilistice sunt analiza de regresie, analiza factorială, analiza varianței, metodele statistice de evaluare a riscurilor, metoda scenariilor etc. Zona metodelor statistice dedicată analizei datelor statistice de natură nenumerică, adică devine din ce în ce mai importantă. rezultate de măsurare pe baza unor caracteristici calitative și diferite. Una dintre principalele aplicații ale statisticii obiectelor de natură nenumerică este teoria și practica expertizelor legate de teoria deciziilor statistice și a problemelor de vot.

Rolul unei persoane atunci când rezolvă probleme folosind metodele teoriei soluțiilor statistice este de a enunța problema, adică de a reduce o problemă reală la cea standard corespunzătoare, de a determina probabilitățile evenimentelor pe baza datelor statistice și, de asemenea, de a aproba soluția optimă rezultată.

În multe cazuri, în știința minieră este necesar să se studieze nu numai procesele deterministe, ci și aleatorii. Toate procesele geomecanice au loc în condiții în continuă schimbare, când anumite evenimente pot să apară sau nu. În acest caz, devine necesară analizarea conexiunilor aleatorii.

În ciuda naturii aleatorii a evenimentelor, ele sunt supuse anumitor tipare, discutate în teoria probabilității , care studiază distribuțiile teoretice ale variabilelor aleatoare și caracteristicile acestora. O altă știință, așa-numita statistică matematică, se ocupă de metode de procesare și analiză a evenimentelor empirice aleatoare. Aceste două științe conexe constituie o teorie matematică unificată a proceselor aleatorii în masă, utilizată pe scară largă în cercetarea științifică.

Elemente de teoria probabilității și statistică matematică. Sub totalitate înțelegeți setul de evenimente omogene ale unei variabile aleatorii X, care constituie materialul statistic primar. Populația poate fi generală (eșantion mare N), care conține o mare varietate de opțiuni pentru un fenomen de masă și selective (probă mică N 1), care reprezintă doar o parte a populației generale.

Probabilitate R(X) evenimente X numit raportul dintre numărul de cazuri N(X) care conduc la producerea unui eveniment X, la numărul total de cazuri posibile N:

În statistica matematică, un analog al probabilității este conceptul de frecvență a evenimentelor, care este raportul dintre numărul de cazuri în care a avut loc evenimentul și numărul total de evenimente:

Cu o creștere nelimitată a numărului de evenimente, frecvența tinde spre probabilitate R(X).

Să presupunem că există câteva date statistice prezentate sub forma unei serii de distribuție (histogramă) în Fig. 4.11, atunci frecvența caracterizează probabilitatea ca o variabilă aleatoare să apară în interval і , iar curba netedă se numește funcție de distribuție.

Probabilitatea unei variabile aleatoare este o evaluare cantitativă a posibilității apariției acesteia. Un eveniment de încredere are R=1, eveniment imposibil – R=0. Prin urmare, pentru un eveniment aleatoriu și suma probabilităților tuturor valorilor posibile.

În cercetare, nu este suficient să ai o curbă de distribuție, dar trebuie să cunoști și caracteristicile acesteia:

a) media aritmetică – ; (4,53)

b) domeniul de aplicare - R= X max – X min , care poate fi folosit pentru a estima aproximativ variația evenimentelor, unde X max si X min – valori extreme ale valorii măsurate;

c) așteptarea matematică – . (4,54)

Pentru variabile aleatoare continue, așteptarea matematică este scrisă sub formă

, (4.55)

acestea. egală cu valoarea reală a evenimentelor observate X, iar abscisa corespunzătoare așteptării se numește centrul distribuției.

d) dispersie - , (4.56)

care caracterizează dispersia unei variabile aleatoare în raport cu așteptarea matematică. Varianta unei variabile aleatoare se mai numește și moment central de ordinul doi.

Pentru o variabilă aleatoare continuă, varianța este egală cu

; (4.57)

e) abaterea standard sau standard -

e) coeficient de variație (dispersie relativă) –

, (4.59)

care caracterizează intensitatea împrăștierii în diferite populații și este folosită pentru a le compara.

Aria de sub curba de distribuție corespunde unității, ceea ce înseamnă că curba acoperă toate valorile variabilelor aleatoare. Cu toate acestea, se poate construi un număr mare de astfel de curbe care vor avea o zonă egală cu unitatea, adică pot avea împrăștiere diferită. Măsura dispersiei este dispersia sau abaterea standard (Fig. 4.12).

Mai sus am examinat principalele caracteristici ale curbei de distribuție teoretică, care sunt analizate prin teoria probabilității. În statistică, acestea operează cu distribuții empirice, iar sarcina principală a statisticii este selectarea curbelor teoretice conform legii distribuției empirice existente.

Să se obțină o serie variațională ca rezultat al n măsurători ale unei variabile aleatorii X 1 , X 2 , X 3 , …x n. Prelucrarea unor astfel de serii se reduce la următoarele operații:

- grup x iîn interval și setați frecvențe absolute și relative pentru fiecare dintre ele;

– se construiește o histogramă pas pe baza valorilor (Fig. 4.11);

– calculați caracteristicile curbei de distribuție empirică: medie aritmetică, varianță D= ; deviație standard.

Valori DȘi s distribuția empirică corespunde valorilor, D(X) Și s(X) distribuţia teoretică.

Să ne uităm la curbele de distribuție teoretice de bază. Cel mai adesea în cercetare se folosește legea distribuției normale (Fig. 4.13), a cărei ecuație are forma:

(4.60)

Dacă combinați axa de coordonate cu punctul m, adică Accept m(X)=0 și acceptați , legea distribuției normale va fi descrisă printr-o ecuație mai simplă:

Pentru a estima împrăștierea, se utilizează de obicei cantitatea . Mai putin s,cu cât se împrăștie mai puțin, adică observațiile diferă puțin unele de altele. Cu crestere sîmprăștierea crește, probabilitatea erorilor crește, iar maximul curbei (ordonatei), egal cu , scade. Prin urmare valoarea la=1/ la 1 se numește o măsură a preciziei. Abaterile standard corespund punctelor de inflexiune (zona umbrită în Fig. 4.12) ale curbei de distribuție.

Atunci când se analizează multe procese aleatorii discrete, se utilizează distribuția Poisson (evenimente pe termen scurt care au loc pe unitatea de timp). Probabilitatea de apariție a numărului de evenimente rare X=1, 2, ... pentru o anumită perioadă de timp este exprimată prin legea lui Poisson (vezi Fig. 4.14):

, (4.62)

Unde X– numărul de evenimente pentru o anumită perioadă de timp t;

λ – densitate, adică numărul mediu de evenimente pe unitatea de timp;

– numărul mediu de evenimente în timp t;

Pentru legea lui Poisson, varianța este egală cu așteptarea matematică a numărului de apariții ale evenimentelor în timp t, adică .

Pentru a studia caracteristicile cantitative ale unor procese (timpul defecțiunilor mașinii etc.), se folosește o lege de distribuție exponențială (Fig. 4.15), a cărei densitate de distribuție este exprimată prin dependență.

Unde λ – intensitatea (numărul mediu) de evenimente pe unitatea de timp.

În distribuția exponențială, intensitatea λ este reciproca așteptării matematice λ = 1/m(X). În plus, relația este valabilă.

Legea distribuției Weibull este utilizată pe scară largă în diverse domenii de cercetare (Fig. 4.16):

, (4.64)

Unde n, μ , – parametrii legii; X– argument, cel mai adesea timp.

La studierea proceselor asociate cu o scădere treptată a parametrilor (scăderea rezistenței rocii în timp etc.), se aplică legea distribuției gamma (Fig. 4.17):

, (4.65)

Unde λ , A- Opțiuni. Dacă A=1, funcția gamma se transformă într-o lege exponențială.

Pe lângă legile de mai sus, se mai folosesc și alte tipuri de distribuții: Pearson, Rayleigh, distribuție beta etc.

Analiza variatiei.În cercetare apare adesea întrebarea: în ce măsură acest sau acel factor aleatoriu influențează procesul studiat? Metodele de stabilire a factorilor principali și influența acestora asupra procesului studiat sunt discutate într-o secțiune specială de teoria probabilităților și statistică matematică - analiza varianței. Există o distincție între analiza unui factor și analiza multifactorială. Analiza varianței se bazează pe utilizarea legii distribuției normale și pe ipoteza că centrele distribuțiilor normale ale variabilelor aleatoare sunt egale. Prin urmare, toate măsurătorile pot fi considerate ca un eșantion din aceeași populație normală.

Teoria fiabilității. Metodele teoriei probabilităților și statisticii matematice sunt adesea folosite în teoria fiabilității, care este utilizată pe scară largă în diferite ramuri ale științei și tehnologiei. Fiabilitatea este înțeleasă ca proprietatea unui obiect de a îndeplini funcții specificate (menținerea indicatorilor de performanță stabiliți) pentru perioada de timp necesară. În teoria fiabilității, eșecurile sunt considerate evenimente aleatorii. Pentru o descriere cantitativă a defecțiunilor se folosesc modele matematice - funcții de distribuție a intervalelor de timp (distribuție normală și exponențială, Weibull, distribuții gamma). Sarcina este de a găsi probabilitățile diferiților indicatori.

Metoda Monte Carlo. Pentru a studia procese complexe de natură probabilistică se utilizează metoda Monte Carlo, prin care se rezolvă problemele de găsire a celei mai bune soluții dintr-o varietate de opțiuni luate în considerare.

Metoda Monte Carlo este numită și metoda de modelare statistică. Aceasta este o metodă numerică, se bazează pe utilizarea numerelor aleatoare care simulează procese probabilistice. Baza matematică a metodei este legea numerelor mari, care se formulează după cum urmează: cu un număr mare de teste statistice, probabilitatea ca media aritmetică a unei variabile aleatoare să tindă spre așteptările ei matematice, este egal cu 1:

, (4.64)

unde ε este orice număr pozitiv mic.

Secvența de rezolvare a problemelor folosind metoda Monte Carlo:

– colectarea, prelucrarea și analiza observațiilor statistice;

– selectarea factorilor principali și a factorilor secundari eliminatori și întocmirea unui model matematic;

– elaborarea algoritmilor și rezolvarea problemelor pe calculator.

Pentru a rezolva probleme folosind metoda Monte Carlo, trebuie să aveți o serie statistică, să cunoașteți legea distribuției sale, valoarea medie, așteptarea matematică și abaterea standard. Soluția este eficientă doar cu utilizarea unui computer.

Trimiteți-vă munca bună în baza de cunoștințe este simplu. Utilizați formularul de mai jos

Studenții, studenții absolvenți, tinerii oameni de știință care folosesc baza de cunoștințe în studiile și munca lor vă vor fi foarte recunoscători.

postat pe http://www.allbest.ru/

Introducere

1. Distribuția chi-pătrat

Concluzie

Aplicație

Introducere

Cum sunt abordările, ideile și rezultatele teoriei probabilităților folosite în viața noastră? teoria pătratului matematic

Teoria probabilității permite utilizarea unei probabilități pentru a calcula altele de interes pentru cercetător.

Un model probabilistic al unui fenomen sau proces este fundamentul statisticii matematice. Sunt utilizate două serii paralele de concepte - cele legate de teorie (model probabilistic) și cele legate de practică (eșantionarea rezultatelor observației). De exemplu, probabilitatea teoretică corespunde frecvenței găsite din eșantion. Aşteptările matematice (seria teoretică) corespunde mediei aritmetice eşantionului (seria practică). De regulă, caracteristicile eșantionului sunt estimări ale celor teoretice. În același timp, cantitățile legate de seria teoretică „sunt în capul cercetătorilor”, se referă la lumea ideilor (conform filosofului grec antic Platon) și nu sunt disponibile pentru măsurare directă. Cercetătorii au doar date eșantion cu care încearcă să stabilească proprietățile unui model probabilistic teoretic care îi interesează.

Deci, utilizarea modelelor probabilistice bazate pe estimarea și testarea ipotezelor folosind caracteristicile eșantionului este esența metodelor probabilistic-statistice de luare a deciziilor.

1. Distribuția chi-pătrat

Folosind distribuția normală, sunt definite trei distribuții care sunt acum adesea folosite în procesarea datelor statistice. Acestea sunt distribuțiile Pearson („chi-pătrat”), Student și Fisher.

Ne vom concentra pe distribuție („chi-pătrat”). Această distribuție a fost studiată pentru prima dată de astronomul F. Helmert în 1876. În legătură cu teoria erorii gaussiene, el a studiat sumele pătratelor a n variabile aleatoare independente distribuite normal normal. Mai târziu, Karl Pearson a dat numele „chi-pătrat” acestei funcții de distribuție. Și acum distribuția îi poartă numele.

Datorită legăturii sale strânse cu distribuția normală, distribuția h2 joacă un rol important în teoria probabilităților și statistica matematică. Distribuția h2 și multe alte distribuții care sunt determinate de distribuția h2 (de exemplu, distribuția Student), descriu distribuțiile eșantioane ale diferitelor funcții din rezultatele observațiilor distribuite în mod normal și sunt utilizate pentru a construi intervale de încredere și teste statistice.

Distribuția Pearson (chi - pătrat) - distribuția unei variabile aleatoare, unde X1, X2,..., Xn sunt variabile aleatoare independente normale, iar așteptarea matematică a fiecăreia dintre ele este zero, iar abaterea standard este una.

Suma patratelor

distribuite conform legii („chi - pătrat”).

În acest caz, numărul de termeni, adică n se numește „numărul de grade de libertate” al distribuției chi-pătrat. Pe măsură ce numărul de grade de libertate crește, distribuția se apropie încet de normal.

Densitatea acestei distribuții

Deci, distribuția h2 depinde de un parametru n - numărul de grade de libertate.

Funcția de distribuție h2 are forma:

dacă h2?0. (2.7.)

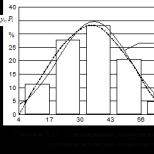
Figura 1 prezintă un grafic al funcțiilor de densitate de probabilitate și distribuție h2 pentru diferite grade de libertate.

Figura 1 Dependența densității de probabilitate q (x) în distribuția h2 (chi - pătrat) pentru diferite numere de grade de libertate

Momente ale distribuției chi-pătrat:

Distribuția chi-pătrat este utilizată în estimarea varianței (folosind un interval de încredere), testarea ipotezelor de acord, omogenitate, independență, în primul rând pentru variabile calitative (categorizate) care iau un număr finit de valori și în multe alte sarcini de analiză a datelor statistice. .

2. „Chi-pătrat” în probleme de analiză a datelor statistice

Metodele statistice de analiză a datelor sunt utilizate în aproape toate domeniile activității umane. Sunt folosite ori de câte ori este necesar pentru a obține și justifica orice judecăți despre un grup (obiecte sau subiecți) cu o oarecare eterogenitate internă.

Etapa modernă de dezvoltare a metodelor statistice poate fi numărată din 1900, când englezul K. Pearson a fondat revista „Biometrika”. Prima treime a secolului XX. trecută sub semnul statisticii parametrice. Metodele au fost studiate pe baza analizei datelor din familiile parametrice de distribuții descrise de curbele familiei Pearson. Cea mai populară a fost distribuția normală. Pentru a testa ipotezele, au fost utilizate testele Pearson, Student și Fisher. Au fost propuse metoda probabilității maxime și analiza varianței și au fost formulate ideile de bază ale planificării experimentului.

Distribuția chi-pătrat este una dintre cele mai utilizate în statistică pentru testarea ipotezelor statistice. Pe baza distribuției chi-pătrat, se construiește unul dintre cele mai puternice teste de bunătate a potrivirii - testul Pearson chi-pătrat.

Criteriul acordului este criteriul de testare a ipotezei despre legea presupusă a unei distribuții necunoscute.

Testul h2 ("chi-pătrat") este folosit pentru a testa ipoteza diferitelor distribuții. Aceasta este demnitatea lui.

Formula de calcul a criteriului este egală cu

unde m și m" sunt frecvențe empirice și, respectiv, teoretice

distribuția în cauză;

n este numărul de grade de libertate.

Pentru a verifica, trebuie să comparăm frecvențele empirice (observate) și teoretice (calculate în ipoteza unei distribuții normale).

Dacă frecvențele empirice coincid complet cu frecvențele calculate sau așteptate, S (E - T) = 0 și criteriul h2 va fi, de asemenea, egal cu zero. Dacă S (E - T) nu este egal cu zero, aceasta va indica o discrepanță între frecvențele calculate și frecvențele empirice ale seriei. În astfel de cazuri, este necesar să se evalueze semnificația criteriului h2, care teoretic poate varia de la zero la infinit. Acest lucru se realizează prin compararea valorii reale a lui h2f cu valoarea sa critică (h2st).Ipoteza nulă, adică ipoteza că discrepanța dintre frecvențele empirice și teoretice sau așteptate este aleatorie, este infirmată dacă h2f este mai mare sau egală cu h2st. pentru nivelul de semnificație acceptat (a) și numărul de grade de libertate (n).

Distribuția valorilor probabile ale variabilei aleatoare h2 este continuă și asimetrică. Depinde de numărul de grade de libertate (n) și se apropie de o distribuție normală pe măsură ce crește numărul de observații. Prin urmare, aplicarea criteriului h2 la evaluarea distribuțiilor discrete este asociată cu unele erori care îi afectează valoarea, în special pe eșantioane mici. Pentru a obține estimări mai precise, eșantionul distribuit în seria de variații trebuie să aibă cel puțin 50 de opțiuni. Aplicarea corectă a criteriului h2 necesită, de asemenea, ca frecvențele variantelor din clasele extreme să nu fie mai mici de 5; dacă sunt mai puțin de 5, atunci acestea sunt combinate cu frecvențele claselor învecinate, astfel încât suma totală să fie mai mare sau egală cu 5. În funcție de combinația de frecvențe, numărul claselor (N) scade. Numărul de grade de libertate se stabilește prin numărul secundar de clase, ținând cont de numărul de restricții asupra libertății de variație.

Deoarece acuratețea determinării criteriului h2 depinde în mare măsură de acuratețea calculării frecvențelor teoretice (T), frecvențele teoretice nerotunjite ar trebui utilizate pentru a obține diferența dintre frecvențele empirice și cele calculate.

Ca exemplu, să luăm un studiu publicat pe un site dedicat aplicării metodelor statistice în științe umaniste.

Testul Chi-pătrat vă permite să comparați distribuțiile de frecvență indiferent dacă sunt distribuite în mod normal sau nu.

Frecvența se referă la numărul de apariții ale unui eveniment. De obicei, frecvența de apariție a evenimentelor este tratată atunci când variabilele sunt măsurate pe o scară de nume, iar celelalte caracteristici ale acestora, în afară de frecvență, sunt imposibil sau problematic de selectat. Cu alte cuvinte, atunci când o variabilă are caracteristici calitative. De asemenea, mulți cercetători tind să convertească scorurile testelor în niveluri (mare, medie, scăzută) și să construiască tabele de distribuție a scorurilor pentru a afla numărul de persoane la aceste niveluri. Pentru a demonstra că într-unul dintre niveluri (într-una dintre categorii) numărul de persoane este într-adevăr mai mare (mai puțin) se folosește și coeficientul Chi-pătrat.

Să ne uităm la cel mai simplu exemplu.

A fost efectuat un test în rândul adolescenților mai tineri pentru a identifica stima de sine. Scorurile testelor au fost convertite în trei niveluri: mare, mediu, scăzut. Frecvențele au fost distribuite după cum urmează:

Mare (B) 27 de persoane.

Medie (C) 12 persoane.

Scăzut (L) 11 persoane

Este evident că majoritatea copiilor au o stima de sine ridicată, dar acest lucru trebuie dovedit statistic. Pentru a face acest lucru, folosim testul Chi-pătrat.

Sarcina noastră este să verificăm dacă datele empirice obţinute diferă de cele la fel de probabile teoretic. Pentru a face acest lucru, trebuie să găsiți frecvențele teoretice. În cazul nostru, frecvențele teoretice sunt frecvențe la fel de probabile, care se găsesc adunând toate frecvențele și împărțind la numărul de categorii.

În cazul nostru:

(B + C + H)/3 = (27+12+11)/3 = 16,6

Formula pentru calculul testului chi-pătrat:

h2 = ?(E - T)I / T

Construim tabelul:

Empiric (E)	Teoretic (T)	(E - T)I / T

Aflați suma ultimei coloane:

Acum trebuie să găsiți valoarea critică a criteriului folosind tabelul cu valori critice (Tabelul 1 din Anexă). Pentru a face acest lucru avem nevoie de numărul de grade de libertate (n).

n = (R - 1) * (C - 1)

unde R este numărul de rânduri din tabel, C este numărul de coloane.

În cazul nostru, există o singură coloană (adică frecvențele empirice originale) și trei rânduri (categorii), așa că formula se schimbă - excludem coloanele.

n = (R - 1) = 3-1 = 2

Pentru probabilitatea de eroare p?0,05 și n = 2, valoarea critică este h2 = 5,99.

Valoarea empirică obținută este mai mare decât valoarea critică - diferențele de frecvențe sunt semnificative (h2 = 9,64; p? 0,05).

După cum puteți vedea, calcularea criteriului este foarte simplă și nu necesită mult timp. Valoarea practică a testului chi-pătrat este enormă. Această metodă este cea mai valoroasă atunci când se analizează răspunsurile la chestionare.

Să ne uităm la un exemplu mai complex.

De exemplu, un psiholog vrea să știe dacă este adevărat că profesorii sunt mai părtinitori față de băieți decât față de fete. Acestea. mai probabil să laude fetele. Pentru a face acest lucru, psihologul a analizat caracteristicile elevilor scrise de profesori pentru frecvența de apariție a trei cuvinte: „activ”, „diligent”, „disciplinat” și au fost numărate și sinonimele cuvintelor.

Datele privind frecvența de apariție a cuvintelor au fost introduse în tabel:

Pentru a procesa datele obținute folosim testul chi-pătrat.

Pentru a face acest lucru, vom construi un tabel de distribuție a frecvențelor empirice, i.e. acele frecvențe pe care le observăm:

Teoretic, ne așteptăm ca frecvențele să fie distribuite egal, adică frecvența va fi distribuită proporțional între băieți și fete. Să construim un tabel de frecvențe teoretice. Pentru a face acest lucru, înmulțiți suma rândurilor cu suma coloanei și împărțiți numărul rezultat la suma totală (e).

Tabelul final pentru calcule va arăta astfel:

		Empiric (E)	Teoretic (T)	(E - T)I / T
băieți	"Activ"
"Harnic"
"Disciplinat"
	"Activ"
"Harnic"
"Disciplinat"
Suma: 4,21

h2 = ?(E - T)I / T

unde R este numărul de rânduri din tabel.

În cazul nostru, chi-pătrat = 4,21; n = 2.

Folosind tabelul de valori critice ale criteriului, găsim: cu n = 2 și un nivel de eroare de 0,05, valoarea critică h2 = 5,99.

Valoarea rezultată este mai mică decât valoarea critică, ceea ce înseamnă că ipoteza nulă este acceptată.

Concluzie: profesorii nu acordă importanță genului copilului atunci când scriu caracteristici pentru el.

Concluzie

Studenții din aproape toate specialitățile studiază secțiunea „Teoria probabilității și statistica matematică” la sfârșitul cursului superior de matematică; în realitate, se familiarizează doar cu unele concepte și rezultate de bază, care în mod clar nu sunt suficiente pentru munca practică. Studenții sunt introduși în unele metode de cercetare matematică în cadrul unor cursuri speciale (de exemplu, „Prognoză și planificare tehnică și economică”, „Analiza tehnică și economică”, „Controlul calității produselor”, „Marketing”, „Control”, „Metode matematice de prognoză”. ”)”, „Statistică”, etc. - în cazul studenților specialităților economice), însă, prezentarea în majoritatea cazurilor este foarte prescurtată și de natură formulatică. Ca urmare, cunoștințele specialiștilor în statistică aplicată sunt insuficiente.

De aceea, cursul „Statistică aplicată” în universitățile tehnice este de mare importanță, iar cursul „Econometrie” în universitățile economice, întrucât econometria este, după cum se știe, analiza statistică a datelor economice specifice.

Teoria probabilității și statistica matematică oferă cunoștințe fundamentale pentru statistica aplicată și econometrie.

Sunt necesare specialiștilor pentru lucrări practice.

M-am uitat la modelul probabilistic continuu și am încercat să-i arăt utilizarea cu exemple.

Și la sfârșitul lucrării mele, am ajuns la concluzia că implementarea competentă a procedurilor de bază de analiză a datelor matematico-statice și testarea statică a ipotezelor este imposibilă fără cunoașterea modelului chi-pătrat, precum și capacitatea de a-l folosi. masa.

Bibliografie

1. Orlov A.I. Statistici aplicate. M.: Editura „Examen”, 2004.

2. Gmurman V.E. Teoria Probabilității și Statistica Matematică. M.: Şcoala superioară, 1999. - 479 p.

3. Ayvozyan S.A. Teoria probabilității și statistică aplicată, vol. 1. M.: Unitate, 2001. - 656 p.

4. Khamitov G.P., Vedernikova T.I. Probabilități și statistici. Irkutsk: BGUEP, 2006 - 272 p.

5. Ezhova L.N. Econometrie. Irkutsk: BGUEP, 2002. - 314 p.

6. Mosteller F. Cincizeci de probleme probabilistice distractive cu soluții. M.: Nauka, 1975. - 111 p.

7. Mosteller F. Probabilitate. M.: Mir, 1969. - 428 p.

8. Yaglom A.M. Probabilitate și informație. M.: Nauka, 1973. - 511 p.

9. Chistiakov V.P. Curs de teoria probabilității. M.: Nauka, 1982. - 256 p.

10. Kremer N.Sh. Teoria Probabilității și Statistica Matematică. M.: UNITATEA, 2000. - 543 p.

11. Enciclopedia matematică, vol.1. M.: Enciclopedia Sovietică, 1976. - 655 p.

12. http://psystat.at.ua/ - Statistică în psihologie și pedagogie. Articolul Testul chi-pătrat.

Aplicație

Puncte critice de distribuție h2

tabelul 1

Postat pe Allbest.ru

...

Documente similare

Modelul probabilistic și axiomatica lui A.N. Kolmogorov. Variabile aleatoare și vectori, problema limită clasică a teoriei probabilităților. Prelucrarea primară a datelor statistice. Estimări punctuale ale caracteristicilor numerice. Testarea statistică a ipotezelor.

manual de instruire, adăugat la 03/02/2010

Reguli de efectuare și finalizare a testelor pentru departamentul de corespondență. Teme și exemple de rezolvare a problemelor de statistică matematică și teoria probabilităților. Tabele de date de referință ale distribuțiilor, densitatea distribuției normale standard.

manual de instruire, adăugat 29.11.2009

Metode de bază de descriere formalizată și analiză a fenomenelor aleatorii, prelucrarea și analiza rezultatelor experimentelor fizice și numerice în teoria probabilităților. Concepte de bază și axiome ale teoriei probabilităților. Concepte de bază ale statisticii matematice.

curs de prelegeri, adăugat 04.08.2011

Determinarea legii distribuției de probabilitate a rezultatelor măsurătorilor în statistica matematică. Verificarea conformităţii distribuţiei empirice cu cea teoretică. Determinarea intervalului de încredere în care se află valoarea mărimii măsurate.

lucrare curs, adăugată 02.11.2012

Convergența secvențelor de variabile aleatoare și a distribuțiilor de probabilitate. Metoda funcţiilor caracteristice. Testarea ipotezelor statistice și efectuarea teoremei limitei centrale pentru secvențe date de variabile aleatoare independente.

lucrare de curs, adăugată 13.11.2012

Principalele etape ale procesării datelor din observații naturale folosind metoda statisticii matematice. Evaluarea rezultatelor obținute, utilizarea acestora în luarea deciziilor de management în domeniul conservării naturii și managementului mediului. Testarea ipotezelor statistice.

lucrare practica, adaugata 24.05.2013

Esența legii distribuției și aplicarea ei practică pentru rezolvarea problemelor statistice. Determinarea varianței unei variabile aleatoare, așteptarea matematică și abaterea standard. Caracteristicile analizei unidirecționale a varianței.

test, adaugat 12.07.2013

Probabilitatea și definiția ei generală. Teoreme de adunare și înmulțire a probabilității. Variabile aleatoare discrete și caracteristicile lor numerice. Legea numerelor mari. Distribuția statistică a eșantionului. Elemente de analiză de corelare și regresie.

curs de prelegeri, adăugat 13.06.2015

Programul cursului, concepte și formule de bază ale teoriei probabilităților, rațiunea și semnificația acestora. Locul și rolul statisticii matematice în disciplină. Exemple și explicații pentru rezolvarea celor mai frecvente probleme pe diverse teme din aceste discipline academice.

manual de instruire, adăugat 15.01.2010

Teoria probabilității și statistica matematică sunt științe ale metodelor de analiză cantitativă a fenomenelor aleatoare de masă. Setul de valori ale unei variabile aleatoare se numește eșantion, iar elementele setului sunt numite valori ale eșantionului unei variabile aleatoare.

Grupul de metode luate în considerare este cel mai important în cercetarea sociologică; aceste metode sunt utilizate în aproape orice studiu sociologic care poate fi considerat cu adevărat științific. Acestea vizează în principal identificarea tiparelor statistice în informațiile empirice, de ex. tipare care sunt îndeplinite „în medie”. De fapt, sociologia se ocupă de studiul „persoanei medii”. În plus, un alt scop important al utilizării metodelor probabiliste și statistice în sociologie este acela de a evalua fiabilitatea eșantionului. Cât de multă încredere există că eșantionul oferă rezultate mai mult sau mai puțin precise și care este eroarea concluziilor statistice?

Obiectul principal de studiu la aplicarea metodelor probabilistice și statistice este variabile aleatoare. Luarea unei variabile aleatoare la o anumită valoare este eveniment aleatoriu– un eveniment care, dacă sunt îndeplinite aceste condiții, poate sau nu să se producă. De exemplu, dacă un sociolog realizează sondaje în domeniul preferințelor politice pe o stradă a orașului, atunci evenimentul „următorul respondent se dovedește a fi un susținător al partidului la putere” este aleatoriu dacă nimic din respondent nu a dezvăluit anterior preferințele sale politice. . Dacă un sociolog a intervievat un respondent în apropierea clădirii Dumei Regionale, atunci evenimentul nu mai este întâmplător. Este caracterizat un eveniment aleatoriu probabilitate ofensiva lui. Spre deosebire de problemele clasice care implică combinații de zaruri și cărți predate în cursurile de probabilitate, în cercetarea sociologică calcularea probabilității nu este atât de simplă.

Cea mai importantă bază pentru evaluarea empirică a probabilității este tendinţa frecvenţei spre probabilitate, dacă prin frecvență înțelegem raportul dintre de câte ori a avut loc un eveniment și de câte ori ar fi putut avea loc teoretic. De exemplu, dacă dintre 500 de respondenți selectați aleatoriu pe străzile orașului, 220 s-au dovedit a fi susținători ai partidului la putere, atunci frecvența de apariție a acestor respondenți este de 0,44. Când eşantion reprezentativ de mărime suficient de mare vom obține probabilitatea aproximativă a unui eveniment sau proporția aproximativă de oameni care posedă o trăsătură dată. În exemplul nostru, cu un eșantion bine selectat, constatăm că aproximativ 44% dintre cetățeni sunt susținători ai partidului la putere. Desigur, din moment ce nu toți cetățenii au fost chestionați, iar unii au mințit în timpul sondajului, există o eroare.

Să luăm în considerare câteva probleme care apar în analiza statistică a datelor empirice.

Estimarea distribuției mărimii

Dacă o anumită caracteristică poate fi exprimată cantitativ (de exemplu, activitatea politică a unui cetățean ca valoare care arată de câte ori a participat în ultimii cinci ani la alegeri la diferite niveluri), atunci sarcina poate fi stabilită pentru a evalua legea distribuției. a acestei caracteristici ca variabilă aleatoare. Cu alte cuvinte, legea distribuției arată ce valori ia mai des o cantitate și care mai rar și cât de des/mai puțin des. Cel mai adesea întâlnit atât în tehnologie și natură, cât și în societate legea distributiei normale. Formula și proprietățile sale sunt prezentate în orice manual de statistică, iar în Fig. 10.1 arată aspectul graficului - este o curbă „în formă de clopot”, care poate fi mai „întinsă” în sus sau mai „untată” de-a lungul axei valorilor variabilei aleatoare. Esența legii normale este că cel mai adesea o variabilă aleatorie ia valori apropiate de o valoare „centrală”, numită așteptări matematice, și cu cât mai departe de ea, cu atât valoarea „ajunge” mai rar acolo.

Există multe exemple de distribuții care pot fi acceptate ca normale cu o mică eroare. În secolul al XIX-lea. Omul de știință belgian A. Quetelet și englezul F. Galton au demonstrat că distribuția de frecvență a oricărui indicator demografic sau antropometric (speranța de viață, înălțimea, vârsta la căsătorie etc.) se caracterizează printr-o distribuție „în formă de clopot”. Același F. Galton și adepții săi au demonstrat că caracteristicile psihologice, de exemplu, abilitățile, respectă legea normală.

Orez. 10.1.

Exemplu

Cel mai frapant exemplu de distribuție normală în sociologie se referă la activitatea socială a oamenilor. Conform legii distribuției normale, se dovedește că oamenii activi social din societate sunt de obicei aproximativ 5-7%. Toți acești oameni activi social merg la mitinguri, conferințe, seminarii etc. Aproximativ același număr sunt excluși de la participarea la viața socială. Majoritatea oamenilor (80–90%) par să fie indiferenți față de politică și viața publică, dar urmează procesele care îi interesează, deși în general au o atitudine detașată față de politică și societate și nu manifestă activitate semnificativă. Astfel de oameni ratează majoritatea evenimentelor politice, dar se uită ocazional la știri la televizor sau pe internet. De asemenea, merg la vot la cele mai importante alegeri, mai ales dacă sunt „amenințați cu un băț” sau „încurajați cu un morcov”. Membrii acestor 80–90% sunt aproape inutili individual din punct de vedere socio-politic, dar centrele de cercetare sociologică sunt destul de interesate de acești oameni, deoarece sunt foarte mulți, iar preferințele lor nu pot fi ignorate. Același lucru este valabil și pentru organizațiile pseudoștiințifice care efectuează cercetări pe comenzile politicienilor sau corporațiilor comerciale. Iar opinia „maselor gri” asupra problemelor cheie legate de prezicerea comportamentului a multor mii și milioane de oameni la alegeri, precum și în timpul evenimentelor politice acute, în timpul divizării societății și a conflictelor dintre diferite forțe politice, nu este indiferentă. către aceste centre.

Desigur, nu toate valorile sunt distribuite conform distribuției normale. Pe lângă aceasta, cele mai importante în statistica matematică sunt distribuțiile binomiale și exponențiale, distribuțiile Fisher-Snedecor, Chi-pătrat și Student.

Evaluarea relației de caracteristici

Cel mai simplu caz este atunci când pur și simplu trebuie să stabiliți prezența/absența unei conexiuni. Cea mai populară metodă în acest sens este metoda Chi-pătrat. Această metodă se concentrează pe lucrul cu date categorice. De exemplu, acestea sunt în mod clar sexul și starea civilă. Unele date par a fi numerice la prima vedere, dar pot fi „transformate” în date categorice prin împărțirea intervalului de valori în mai multe intervale mici. De exemplu, experiența în fabrică poate fi clasificată ca mai puțin de un an, unul până la trei ani, trei până la șase ani și mai mult de șase ani.

Lasă parametrul X disponibil P valori posibile: (x1,..., X r1), și parametrul YT valori posibile: (y1,..., la T) , q ij este frecvența observată de apariție a perechii ( X eu, la j), adică numărul de apariții detectate ale unei astfel de perechi. Calculăm frecvențele teoretice, i.e. de câte ori ar trebui să apară fiecare pereche de valori pentru cantități absolut neînrudite:

Pe baza frecvențelor observate și teoretice, calculăm valoarea

De asemenea, trebuie să calculați suma grade de libertate conform formulei

Unde m, n– numărul de categorii tabulate. În plus, alegem nivelul de semnificație. Cu cât mai sus fiabilitate dorim să obținem, cu atât nivelul de semnificație trebuie luat mai jos. De obicei, se alege o valoare de 0,05, ceea ce înseamnă că putem avea încredere în rezultate cu o probabilitate de 0,95. În continuare, în tabelele de referință găsim valoarea critică după numărul de grade de libertate și nivelul de semnificație. Dacă , atunci parametrii XȘi Y sunt considerate independente. Dacă , atunci parametrii XȘi Y - dependent. Dacă, atunci este periculos să tragem concluzii despre dependența sau independența parametrilor. În acest din urmă caz, este recomandabil să se efectueze cercetări suplimentare.

De asemenea, rețineți că testul Chi-pătrat poate fi utilizat cu o încredere foarte mare numai atunci când toate frecvențele teoretice nu sunt sub un anumit prag, care este de obicei considerat a fi 5. Fie v frecvența teoretică minimă. Pentru v > 5, testul Chi-pătrat poate fi folosit cu încredere. Un televizor< 5 использование критерия становится нежелательным. При v ≥ 5 вопрос остается открытым, требуется дополнительное исследование о применимости критерия "Хи-квадрат".

Să dăm un exemplu de utilizare a metodei Chi-pătrat. Să fie, de exemplu, într-un anumit oraș, un sondaj în rândul tinerilor suporteri ai echipelor locale de fotbal și s-au obținut următoarele rezultate (Tabelul 10.1).

Să propunem o ipoteză despre independența preferințelor fotbalistice ale tinerilor orașului N de la genul respondentului la un nivel de semnificație standard de 0,05. Se calculează frecvențele teoretice (Tabelul 10.2).

Tabelul 10.1

Rezultatele sondajului fanilor

Tabelul 10.2

Frecvențe de preferință teoretice

De exemplu, frecvența teoretică pentru fanii de tineret ai Zvezda este obținută ca

în mod similar – alte frecvențe teoretice. Apoi, calculăm valoarea Chi pătrat:

Determinăm numărul de grade de libertate. Pentru un nivel de semnificație de 0,05, căutăm valoarea critică:

Deoarece, iar superioritatea este semnificativă, putem spune aproape sigur că preferințele de fotbal ale băieților și fetelor din oraș N variază foarte mult, cu excepția cazului unui eșantion nereprezentativ, de exemplu, dacă cercetătorul nu a obținut un eșantion din diferite zone ale orașului, limitându-se la intervievarea respondenților din propriul bloc.

O situație mai dificilă este atunci când trebuie să cuantificați puterea conexiunii. În acest caz, metodele sunt adesea folosite analiza corelației. Aceste metode sunt de obicei discutate în cursurile avansate de statistică matematică.

Aproximarea dependențelor folosind date punct

Să existe un set de puncte - date empirice ( X eu, Yi), i = 1, ..., P. Este necesar să se aproximeze dependența reală a parametrului la din parametru X,și, de asemenea, să dezvolte o regulă pentru calcularea valorii y, Când X este situat între două „noduri” Xi.

Există două abordări fundamental diferite pentru rezolvarea problemei. Primul este că dintre funcțiile unei familii date (de exemplu, polinoame), este selectată o funcție al cărei grafic trece prin punctele existente. A doua abordare nu „forța” graficul funcției să treacă prin puncte. Cea mai populară metodă în sociologie și într-o serie de alte științe este metoda celor mai mici pătrate– aparține grupei a doua de metode.

Esența metodei celor mai mici pătrate este următoarea. Având în vedere o familie de funcții la(x, a 1, ..., A t) cu m coeficienți incerti. Este necesară selectarea coeficienților nesiguri prin rezolvarea unei probleme de optimizare

Valoarea minimă a funcției d poate acționa ca o măsură a preciziei de aproximare. Dacă această valoare este prea mare, ar trebui selectată o altă clasă de funcție la sau extinde clasa utilizată. De exemplu, dacă clasa „polinoame de grad nu mai mare de 3” nu a oferit o acuratețe acceptabilă, luăm clasa „polinoame de grad nu mai mare de 4” sau chiar „polinoame de grad nu mai mare de 5”.

Cel mai adesea, metoda este utilizată pentru familia de „polinoame de grad nu mai mare decât N":

De exemplu, când N= 1 este o familie de funcții liniare, cu N = 2 – familia de funcții liniare și pătratice, cu N = 3 – familia de funcții liniare, pătratice și cubice. Lăsa

Apoi coeficienții funcției liniare ( N= 1) sunt căutate ca soluție a unui sistem de ecuații liniare

Coeficienții unei funcții de formă A 0 + a 1x + a 2X 2 (N= 2) sunt căutate ca soluție pentru sistem

Cei care doresc să aplice această metodă la o valoare arbitrară N poate face acest lucru văzând modelul după care sunt compilate sistemele de ecuații date.

Să dăm un exemplu de utilizare a metodei celor mai mici pătrate. Să se modifice numărul unui anumit partid politic după cum urmează:

Se poate observa că schimbările în dimensiunea partidului de-a lungul diferiților ani nu sunt foarte diferite, ceea ce ne permite să aproximăm dependența cu o funcție liniară. Pentru a face mai ușor de calculat, în loc de o variabilă X– an – introduceți o variabilă t = x – 2010, adică Să luăm primul an de numărare drept „zero”. Noi calculăm M 1; M 2:

Acum calculăm M", M*:

Cote A 0, A 1 functii y = a 0t + A 1 sunt calculate ca soluție a sistemului de ecuații

Rezolvând acest sistem, de exemplu, folosind regula lui Cramer sau metoda substituției, obținem: A 0 = 11,12; A 1 = 3,03. Astfel, obținem aproximarea

care vă permite nu numai să operați cu o singură funcție în loc de un set de puncte empirice, ci și să calculați valorile funcției care depășesc limitele datelor inițiale - „pentru a prezice viitorul”.

De asemenea, rețineți că metoda celor mai mici pătrate poate fi utilizată nu numai pentru polinoame, ci și pentru alte familii de funcții, de exemplu, pentru logaritmi și exponențiale:

Gradul de încredere al unui model construit folosind metoda celor mai mici pătrate poate fi determinat pe baza măsurării R-pătrat sau a coeficientului de determinare. Se calculează ca

Aici . Aproape R 2 la 1, cu atât modelul este mai adecvat.

Detectare abere

O valoare anormală a unei serii de date este o valoare anormală care se evidențiază puternic în eșantionul general sau seria generală. De exemplu, procentul cetățenilor unei țări care au o atitudine pozitivă față de un anumit politician să fie în perioada 2008–2013. respectiv 15, 16, 12, 30, 14 și 12%. Este ușor de observat că una dintre valori diferă brusc de toate celelalte. În 2011, ratingul politicianului din anumite motive a depășit cu mult valorile obișnuite, care se situau în intervalul 12-16%. Prezența emisiilor se poate datora diferitelor motive:

1)erori de măsurare;
2) natura neobișnuită a datelor de intrare(de exemplu, când se analizează procentul mediu de voturi primite de un politician; această valoare la o secție de votare dintr-o unitate militară poate diferi semnificativ de valoarea medie a orașului);
3) consecință a legii(valorile care diferă mult de restul se pot datora unei legi matematice - de exemplu, în cazul unei distribuții normale, un obiect cu o valoare mult diferită de medie poate fi inclus în eșantion);
4) dezastre(de exemplu, într-o perioadă de confruntare politică scurtă, dar acută, nivelul activității politice a populației se poate schimba dramatic, așa cum sa întâmplat în timpul „revoluțiilor de culoare” din 2000–2005 și „Primăverii arabe” din 2011);
5) actiuni de control(de exemplu, dacă în anul anterior studiului un politician a luat o decizie foarte populară, atunci în acest an ratingul său poate fi semnificativ mai mare decât în alți ani).

Multe metode de analiză a datelor nu sunt robuste pentru valori aberante, așa că pentru a le utiliza în mod eficient, datele trebuie să fie curățate de valori aberante. Un exemplu izbitor de metodă instabilă este metoda celor mai mici pătrate menționată mai sus. Cea mai simplă metodă de căutare a valorii aberante se bazează pe așa-numitele distanta interquartila. Determinarea intervalului

Unde Q m – sens T- a quartila. Dacă un membru al seriei nu se încadrează în interval, atunci este privit ca o valoare anormală.

Să explicăm cu un exemplu. Semnificația quartilelor este că ele împart o serie în patru grupuri egale sau aproximativ egale: primul cuartil „separă” sfertul din stânga al seriei, sortat în ordine crescătoare, al treilea quartile separă sfertul drept al seriei, al doilea quartile. aleargă în mijloc. Să explicăm cum să căutăm Q 1, și Q 3. Lăsați o serie de numere sortate în ordine crescătoare P valorile. Dacă n + 1 este divizibil cu 4 fără rest, atunci Q k esență k(P+ 1)/termenul 4 al seriei. De exemplu, având în vedere seria: 1, 2, 5, 6, 7, 8, 10, 11, 13, 15, 20, iată numărul de termeni n = 11. Apoi ( P+ 1)/4 = 3, adică primul quartil Q 1 = 5 – al treilea termen al seriei; 3( n + 1)/4 = 9, adică a treia cuartilă Q:i= 13 – al nouălea membru al seriei.

Cazul este un pic mai complicat când n + 1 nu este un multiplu al lui 4. De exemplu, având în vedere seria 2, 3, 5, 6, 7, 8, 9, 30, 32, 100, unde numărul de termeni P= 10. Atunci ( P + 1)/4 = 2,75 -

poziție între al doilea membru al seriei (v2 = 3) și al treilea membru al seriei (v3 = 5). Apoi luăm valoarea 0,75v2 + 0,25v3 = 0,75 3 + 0,25 5 = 3,5 - aceasta va fi Q 1. 3(P+ 1)/4 = 8,25 – poziție între al optulea membru al seriei (v8= 30) și al nouălea membru al seriei (v9=32). Luăm valoarea 0,25v8 + 0,75v9 = 0,25 30 + + 0,75 32 = 31,5 - aceasta va fi Q 3. Există și alte opțiuni de calcul Q 1 și Q 3, dar se recomandă utilizarea opțiunii prezentate aici.

Strict vorbind, în practică, se întâlnește de obicei o lege „aproximativ” normală - deoarece legea normală este definită pentru o mărime continuă de-a lungul întregii axe reale, multe mărimi reale nu pot satisface strict proprietățile mărimilor distribuite normal.
Nasledov A.D. Metode matematice de cercetare psihologică. Analiza și interpretarea datelor: manual, manual. Sankt Petersburg: Rech, 2004. pp. 49–51.
Pentru cele mai importante distribuții ale variabilelor aleatoare, vezi, de exemplu: Orlov A.I. Matematica hazardului: probabilitate și statistică - fapte de bază: manual. indemnizatie. M.: MZ-Press, 2004.