Modelul unei reacții chimice neliniare - atractorul Rössler. Generatori de haos pe plisse. B.9. cartografierea unui cerc pe sine: sincronizarea numărului de rotații și a arborilor de zâne

Să luăm în considerare imaginea unui atractor ciudat al sistemului Rössler.Configurația sa geometrică poate fi vizualizată după cum urmează. Luați o bandă de hârtie care se lărgește spre un capăt (a). La capătul larg, îndoiți banda în jumătate și apoi lipiți-o într-un inel, așa cum se arată în Fig. (b-g). Un astfel de model de hârtie oferă o idee bună despre atractorul Ressler și aranjarea spațială a traiectoriilor sale. Cu toate acestea, este inexact într-un detaliu esențial. Soluția SDE-ului lui Rössler poate fi construită atât înainte, cât și înapoi în timp, iar teorema unicității este valabilă. În consecință, două traiectorii de fază diferite nu pot converge într-una singură, ceea ce înseamnă că procedura de lipire este ilegală.

Rezolvarea contradicției este că „banda” de pe care atractorul Rössler este „lipit împreună” este de fapt o formațiune stratificată, un set de foi. Procedura de lipire echivalează cu stabilirea unei corespondențe unu-la-unu între setul de foi ale benzii originale și setul de foi ale benzii pliate în jumătate. O astfel de corespondență poate avea loc numai dacă ambele mulțimi sunt infinite. Astfel, atractorul Ressler trebuie să aibă un număr infinit de straturi în secțiunea sa transversală și, prin urmare, să reprezinte o structură complexă, așa cum se spune, un obiect fractal.

Același tip de structură este caracteristic altor atractori ciudați. Figura prezintă o diagramă din articolul lui Hainault care ilustrează structura atractorului în cartografiere (2). Se poate remarca faptul că punctul principal în motivarea acestei lucrări a fost tocmai intenția de a prezenta un exemplu mai vizual al structurii fractale a unui atractor pentru a fi luat în considerare decât cel demonstrat de modelul Lorentz cunoscut la acea vreme. Reproducerea structurii fractale a atractorului Hainault la diferite scări de rezoluție

Fractalii Fractalii sunt înțeleși ca mulțimi care demonstrează proprietățile de similitudine (sau invarianța scării) într-un sens strict sau aproximativ la diferite scări de rezoluție ale structurii lor geometrice, precum și obiectele din natură care au această proprietate, cel puțin aproximativ, într-un mod destul de gamă largă de scări. Conceptul de fractal a intrat în uz datorită matematicianului Benoit Mandelbrot pentru a desemna obiecte geometrice netriviale. El a atras atenția asupra faptului că obiectele fractale pot fi considerate nu doar ca „monstri matematici”, ci ca modele ale proprietăților geometrice ale unor formațiuni foarte reale din natură (linie de coastă, nori, lanțuri muntoase, copaci, vârtejuri într-un fluid turbulent etc. .) . Clasificarea fractalilor 1. Constructiv (construit folosind anumite procedee geometrice sau algebrice recursive). 2. Dinamic (generat de sisteme dinamice). 3. Natural (observat în natură). 4. Stochastic (traiectoria unei particule browniene sau o traiectorie arbitrară a unui proces aleator de difuzie).

Cel mai simplu fractal constructiv este asociat cu o construcție propusă în 1883 de fondatorul teoriei mulțimilor, Georg Cantor. Având un segment de unitate, împărțiți-l în trei părți egale și aruncați intervalul care ocupă treimea mijlocie. Împărțim din nou fiecare dintre segmentele rămase în trei părți și aruncăm treimea din mijloc și așa mai departe la infinit. Ceea ce rămâne până la urmă este setul Cantor sau „Praful Cantor”. Mulțimea Cantor satisface definiția unui fractal: fiecare fragment al acestuia, obținut dintr-un anumit segment la un anumit nivel de construcție, este asemănător întregului set și intră în el cu o recalculare adecvată a scalei. Să notăm două proprietăți ale setului Cantor. 1) Acest set are măsura zero (lungime zero), adică lungimea totală a tuturor intervalelor aruncate este egală cu 1, lungimea intervalului inițial. La pasul 1 se aruncă un interval de lungime 1/3, la pasul 2 – două intervale de lungime 1/9, la al n-lea – 2 n intervale de lungime 3 -n+1. Calculând suma, obținem

2) Mulțimea Cantor are cardinalitatea unui continuum, i.e. permite stabilirea unei corespondențe unu-la-unu cu mulțimea tuturor punctelor unui interval unitar datorită algoritmului de construcție a acestuia. Schimbând regula de împărțire a unui segment de unitate și introducerea diviziunii în trei părți inegale, se poate obține o mulțime Cantor mai complexă cu două scale (multifractal). Fulgul de zăpadă Koch este un exemplu de zonă cu o limită fractală. Începem construcția cu un triunghi echilateral. Apoi, pe fiecare parte, înlocuim treimea mijlocie cu o linie întreruptă de două segmente de aceeași lungime. Repetând procedura de multe ori la infinit, ajungem în cele din urmă la un obiect fractal. Primele 4 iterații ale celor 7 pași de construcție a fulgului de zăpadă Koch

Pentru a construi un șervețel (triunghi) Sierpinski, luăm un triunghi echilateral, care poate fi imaginat ca fiind compus din patru triunghiuri mai mici. Aruncă triunghiul din mijloc. Apoi, efectuăm aceleași acțiuni cu fiecare dintre triunghiurile rămase la infinit. Covorul Sierpinski este construit pe baza unui pătrat, care este împărțit în 9 părți egale prin linii verticale și orizontale, iar pătratul din mijloc este aruncat. Cu fiecare pătrat rămas, aceeași procedură și așa mai departe la infinit.

Fractalii generați de dinamica deterministă a sistemelor neliniare sunt numiți dinamici. Fractalii dinamici pot fi atractori sau alte mulțimi limitatoare în spațiul fazelor, a căror dimensiune N pentru fluxuri ar trebui să fie N > 2, iar pentru sisteme cu timp discret N 2. Când vorbesc despre atractori neregulați, ei fac distincția între conceptele „ciudat” și „haotic”. Este proprietatea „ciudățeniei” care se referă la geometria sa non-trivială (fractală). Limitele bazinelor de atracție ale mai multor atractori coexistenți au proprietăți fractale și aceasta este o trăsătură caracteristică a DS neliniară. 2, "> 2, iar pentru sistemele cu timp discret N 2. Când se vorbește despre atractori neregulați, ei separă conceptele de „ciudat” și „haotic”. Este proprietatea „ciudatății” care se referă la non-triviala sa. geometrie (fractală). Limitele au proprietăți fractale bazine de atracție a mai multor atractori coexistenți și aceasta este o trăsătură caracteristică a DS neliniare."> 2, " title=" Fractalii generați de dinamica deterministă a sistemelor neliniare sunt numiți dinamici). Fractalii dinamici pot fi atractori sau alte seturi limitatoare în spațiul fazelor, dimensiunea care N pentru fire ar trebui să fie N > 2,"> title="Fractalii generați de dinamica deterministă a sistemelor neliniare sunt numiți dinamici. Fractalii dinamici pot fi atractori sau alte mulțimi limitatoare în spațiul fazelor, a căror dimensiune N pentru fluxuri ar trebui să fie N > 2,"> !}

Mulți fractali dinamici care sunt renumiti pentru frumusețea lor sunt asociați cu următoarea hartă Julia simplă: unde Z este o variabilă complexă și C este un parametru complex. Mulțimea Julia este un exemplu de graniță fractală între bazinele de atracție ale unui atractor la infinit (regiune maro) și mișcarea periodică (regiune multicoloră). Tonul (culoarea) este determinat de numărul de iterații necesare pentru a ajunge la atractor.

Mulțimea Mandelbrot Această structură fractală se obține prin aplicarea repetată a unei transformări algebrice (relație de recurență) folosind o funcție a unei variabile complexe. Culoarea neagră din mijloc arată că în aceste puncte funcția tinde spre zero - acesta este mulțimea Mandelbrot. În afara acestui set, funcția tinde spre infinit. Cel mai interesant lucru sunt limitele setului. Sunt fractali. La limitele acestui set, funcția se comportă imprevizibil - haotic.

Dimensiunile atractorilor O trăsătură distinctivă a atractorilor ciudați este prezența proprietății invarianței la scară (scalare), care se exprimă în repetabilitatea structurii lor pe scale din ce în ce mai mici. O consecință a legilor similarității este universalitatea în geometria mulțimilor haotice de secțiuni Poincaré, în distribuția energiei de vibrație pe frecvențe și amplitudini din spectru etc. Pentru a caracteriza atractorii ciudați, este introdus conceptul de dimensiune. Dimensiunea determină cantitatea de informații necesară pentru a specifica coordonatele unui punct aparținând atractorului, în limitele preciziei specificate. Pentru atractorii obișnuiți care sunt varietăți, dimensiunea este un număr întreg: un punct fix are dimensiunea 0, un ciclu limită are dimensiunea 1, iar un tor bidimensional are dimensiunea 2. Datorită complexității structurii geometrice, atractorii ciudați nu sunt varietăţi şi au o dimensiune fracţională. Definițiile dimensiunii sunt, în general, împărțite în două tipuri: cele care depind doar de proprietățile metrice ale atractorului și, pe lângă metrică, cele care depind de proprietățile statistice ale fluxului datorită dinamicii. În cazuri tipice, dimensiunile metrice capătă aceeași valoare, care se numește de obicei dimensiunea fractală a atractorului D. Dimensiunea determinată ținând cont de probabilitatea ca traiectoria să viziteze diferite zone ale atractorului în spațiul fazelor se numește informație sau dimensiunea masurii naturale.

(29)

Aplicând definiția (29) pentru a calcula dimensiunile unui punct, a unei linii și a unei suprafețe, puteți verifica valorile obișnuite de 0, 1 și, respectiv, 2. Pentru mulțimile netriviale, dimensiunea fractală este întotdeauna fracțională. Această proprietate este folosită ca semn caracteristic al „ciudații” atractorului. Dimensiunea fractală definită prin acoperirea unui set cu celule de formă și dimensiune fixă ​​se numește capacitatea mulțimii. Dacă elemente de formă și dimensiune arbitrare sunt utilizate pentru a acoperi o mulțime, atunci dimensiunea calculată în acest fel se numește dimensiunea Hausdorff. Pentru fractali, această dimensiune și capacitate coincid și pur și simplu vorbesc despre dimensiunea fractală a obiectului.

Dimensiunea informațională Alături de dimensiunea fractală, sunt introduse și utilizate o serie de altele, inclusiv informații, corelații și dimensiuni Renyi generalizate. De ce nu este suficient doar dimensiunea valorii? Să ne imaginăm că atractorul este eterogen – unele zone (elementele de acoperire) sunt vizitate mai des, altele mai rar. Această împrejurare nu se reflectă în niciun fel în definiția capacității. Să fie definită o măsură invariantă pentru un atractor și am construit o acoperire a acestui atractor, în timp ce fiecare celulă a acoperirii va avea propria sa valoare de măsură specifică. Cu alte cuvinte, fiecare i-a celulă de acoperire va avea o anumită probabilitate de a fi în ea p i. Presupunând că celulele acoperă complet atractorul și nu se suprapun între ele, avem Considerați acum suma (30) Această valoare poate fi interpretată ca cantitatea de informații din afirmația că punctul reprezentativ se găsește într-o celulă de acoperire specifică.

Este clar că pe măsură ce dimensiunea celulelor de acoperire scade, valoarea sumei (30) va crește: cu cât celulele sunt mai mici, cu atât există mai multe informații în afirmația că punctul a căzut într-o anumită celulă. Această creștere urmează legea (31) sau, echivalent, există o limită (32) Mărimea D I se numește dimensiunea informațională.

Dimensiunea de corelație și algoritmul Grassberger-Procaccia Luați în considerare din nou acoperirea atractorului de către celule de aceeași dimensiune și presupuneți că două puncte aparținând atractorului, x 1 și x 2, sunt alese aleatoriu Care este probabilitatea ca ambele va ajunge în celula i-a? Probabilitatea ca un punct să cadă în al i-lea element de acoperire este egală cu p i. Dacă ambele puncte care intră într-o celulă dată pot fi considerate evenimente independente, atunci probabilitatea va fi p i 2. Luați în considerare suma (33). Pe măsură ce dimensiunea celulelor scade, suma va scădea și acest lucru se va întâmpla conform legii puterii. (34) sau, în mod echivalent, există o limită (35) Valoarea lui D C se numește dimensiunea corelației.
Dimensiunea generalizată Puteți generaliza dimensiunile D F, D I, D C și introduceți o dimensiune de ordin q, folosind entropia generalizată de ordin q (entropia Renyi) (37) unde P i este probabilitatea de a detecta un punct de referință în i-lea. elementul de acoperire. Atunci dimensiunea ordinului q este (38) Se poate arăta că D 0 = D F, D 1 = D I, D 2 = D C.

Dimensiunea Lyapunov Dimensiunea fractală a atractorului DS în spațiul de fază R N poate fi estimată folosind spectrul indicilor caracteristici Lyapunov (LCP). Această estimare se numește dimensiunea Lyapunov D L și este dată de o anumită relație numită formula Kaplan-Yorke. Fie cunoscut spectrul LCP al unui atractor ciudat al unui sistem N-dimensional, a cărui dimensiune trebuie estimată: 1 2 ... N. Suma tuturor indicatorilor de spectru este negativă datorită disipativității sistemului. Să luăm în considerare primii k indicatori ai spectrului LCP, unde k este cel mai mare număr care satisface condiția Numărul specificat de indicatori include toți cei pozitivi, toți zero și unii negativi, astfel încât suma să rămână nenegativă. Deoarece suma indicatorilor specifică natura modificării locale a elementului volumului de fază din atractor, atunci volumul de fază de dimensiunea k

Astfel, putem presupune că dimensiunea atractorului se află în intervalul k D L k + 1. Este rezonabil să se ceară ca mișcarea pe atractor să se supună unei condiții care corespunde conceptelor fizice ale staționarității procesului, unde d este partea fracțională a dimensiunii. Dimensiunea Lyapunov completă a atractorului va fi suma părților întregi k și fracționale d: (39) Diferențele în semnătura spectrelor LCP și dimensiunea D L pot fi un semn al clasificării atractorilor obișnuiți și ciudați. Din formula Kaplan-York (39) pentru atractorii obișnuiți obținem următoarele valori ale dimensiunii Lyapunov, care coincid cu dimensiunea fractală a mulțimii corespunzătoare și sunt egale cu numărul de indicatori zero din spectrul LCP: starea de echilibru (-, -, -, ...) – D L = 0; ciclu limită (0, -, -, -, …) – D L = 1; tor bidimensional (0, 0, -, -, …) – D L = 2; Torul N-dimensional (0, 0, 0, …,0, -, …) – D L = N.

Pentru atractorii obișnuiți, următoarele sunt în deplin acord: dimensiunea Lyapunov, dimensiunea fractală și semnătura spectrului LHP a atractorului. În ceea ce privește atractorii ciudați, o astfel de interacțiune poate fi discutată doar în legătură cu sistemele diferențiale tridimensionale și mapările reversibile bidimensionale cu întindere și compresie constantă. S-a dovedit că pentru atractorii din astfel de sisteme, dimensiunea fractală poate fi determinată prin următoarele relații: - pentru mapările bidimensionale - pentru sistemele diferențiale tridimensionale În cazul general, are loc următoarea relație între dimensiuni: Totuși, în limitele erorilor de calcul, putem presupune aproximativ că valorile dimensiunilor coincid. Atunci când alegeți ce definiție a dimensiunii este cea mai bună de utilizat, de obicei se pornește de la posibilitățile de calcule numerice. Când modelați numeric DS, este cel mai convenabil să utilizați dimensiunea Lyapunov. Pentru a estima dimensiunea fractală a unui atractor din datele experimentale, dimensiunea de corelație este cea mai potrivită.

În această carte am adoptat o abordare empirică a oscilațiilor haotice și am conturat o serie de fenomene fizice diferite în care dinamica haotică joacă un rol important. Desigur, nu toți cititorii au acces la un laborator sau o înclinație pentru experimentare, deși majoritatea pot folosi computere digitale. Având în vedere acest lucru, prezentăm în această anexă o serie de experimente numerice, fezabile fie pe un computer personal, fie pe un microcomputer, în speranța că vor ajuta cititorul să exploreze dinamica modelelor haosului de acum clasice.

B.1. ECUAȚIA LOGISTICĂ: DUBLĂ PERIOADA

Una dintre cele mai simple probleme cu care să începem introducerea unor noi dinamici trebuie să fie modelul de creștere a populației sau ecuația logistică.

Fenomenele asociate cu dublarea perioadei au fost observate de diverși cercetători (vezi, de exemplu, lucrarea lui May) și, bineînțeles, de Feigenbaum, care a descoperit celebrele legi ale similitudinii parametrilor (vezi capitolele 1 și 5). Un computer personal facilitează reproducerea a două experimente numerice.

În primul experiment avem un grafic al dependenței de în intervalul . Modul de dublare a perioadei este observat la valorile de mai jos Începând cu veți putea vedea o traiectorie cu o perioadă de 1. Pentru a vedea traiectorii mai lungi, marcați primele 30-50 de iterații cu puncte, iar iterațiile ulterioare cu un simbol diferit.

Desigur, prin trasarea dependenței de , veți putea observa modurile tranzitorii și staționare. Traiectorii haotice pot fi detectate la . În apropiere se poate detecta o traiectorie cu o perioadă de 3.

Următorul experiment numeric este legat de construcția unei diagrame de bifurcație. Pentru a face acest lucru, ar trebui să construiți un grafic al dependenței în general de parametrul de control. Selectați o condiție inițială (de exemplu, și faceți 100 de iterații de mapare. Apoi reprezentați grafic valorile obținute ca urmare a următoarelor 50 de iterații pe axa verticală și valoarea corespunzătoare pe axa orizontală (sau invers). pas de aproximativ 0,01 și treceți prin intervalul On În diagramă, la punctele de dublare a perioadei, ar trebui să obțineți bifurcații clasice de tip furcă. Puteți determina numărul Feigenbaum din datele unui experiment numeric?

May oferă, de asemenea, o listă de experimente numerice cu alte mapări unidimensionale, de exemplu cu maparea

El descrie această cartografiere ca un model de creștere a populației unei singure specii reglementate de o boală epidemică. Explorați zona. Punctul de acumulare a dublărilor perioadei și începutul haosului corespund cu . Lucrarea lui May conține și date despre alte experimente numerice.

B.2. ECUATII LORENTZ

Un experiment numeric remarcabil, fără îndoială demn de repetat, este cuprins în opera originală a lui Lorentz. Lorentz a simplificat ecuațiile derivate de Salzman pe baza ecuațiilor convecției termice într-un lichid (vezi capitolul 3). Prioritatea în descoperirea soluțiilor neperiodice ale ecuațiilor de convecție, așa cum a admis Lorenz, îi aparține lui Salzman. Pentru a studia mișcările haotice, Lorentz a ales valorile acum clasice ale parametrilor din ecuații

Datele prezentate în Fig. 1 și 2 din articolul lui Lorentz pot fi reproduse prin alegerea condițiilor inițiale și a pasului de timp și proiectând soluția fie pe un plan, fie pe un plan

Pentru a obține maparea unidimensională indusă de acest flux, Lorentz a luat în considerare maximele succesive ale variabilei z, pe care a desemnat-o Graficul de dependență, a arătat că în acest caz maparea este dată de o curbă asemănătoare cu forma acoperișului unei case. Lorentz a explorat apoi o versiune simplificată a acestei cartografii, numită „hărțirea tipului casei”, o versiune biliniară a ecuației logistice.

B.3. INTERMITABILITATE ȘI ECUAȚII LORENTZ

Un exemplu clar de intermitență poate fi văzut prin integrarea numerică a ecuațiilor Lorentz folosind un computer:

cu parametri conform metodei Runge-Kutta. Când obțineți o traiectorie periodică, dar când și mai multe „explozii” sau zgomot haotic vor apărea (vezi lucrarea lui Manneville și Pomo). Măsurând numărul mediu N de cicluri periodice între explozii (fază laminară), ar trebui să obțineți legea similarității

B.4. ATRACTOR OENON

O generalizare a mapării pătratice pe o linie pentru cazul bidimensional (pe un plan) a fost propusă de astronomul francez Hénon:

Harta Hénon se reduce la harta logistică studiată de May și Feigenbaum. Valorile lui a și b la care apare un atractor ciudat includ, în special, . Construiți un grafic al acestei mapări pe un plan, limitându-l la un dreptunghi. După ce ați primit un atractor, concentrați-vă atenția pe o zonă mică a acestuia și măriți această zonă folosind o transformare de similaritate. Urmați un număr semnificativ mai mare de iterații de cartografiere și încercați să dezvăluiți o structură fractală la scară mică. Dacă aveți suficientă răbdare sau aveți un computer rapid la îndemână, atunci efectuați o altă transformare de similaritate și repetați-o din nou pentru o zonă și mai mică a atractorului (vezi Fig. 1.20, 1.22).

Dacă aveți un program pentru calcularea exponenților Lyapunov, atunci este util să rețineți că valoarea exponentului Lyapunov este dată în literatură, iar dimensiunea fractală a atractorului din harta Henon este egală cu . Variind parametrii a și b, puteți încerca să determinați intervalul acelor valori la care există atractorul și să găsiți aria de dublare a perioadei în plan (a, b).

B.5. ECUAȚIA DUFFING: ATRACTOR UEDA

Acest model de circuit electric cu inductanță neliniară a fost discutat în capitolul. 3. Ecuațiile acestui model, scrise sub forma unui sistem de ecuații de ordinul întâi, au forma

Oscilațiile haotice din acest model au fost studiate în detaliu de Ueda. Utilizați un algoritm standard de integrare numerică, cum ar fi schema Runge-Kutta de ordinul al patrulea și luați în considerare cazul. Când ar trebui să obțineți o traiectorie periodică cu perioada 3. (Efectuați secțiunea Poincaré la ) În vecinătatea valorii, traiectoria cu perioada 3 ar trebui să intre în mișcare haotică după bifurcare.

La periodicitate se restabilește din nou cu un regim haotic tranzitoriu (vezi Fig. 3.13).

Comparați natura fractală a atractorului pe măsură ce amortizarea scade, presupunând și 0,05. Vă rugăm să rețineți că la , rămâne doar o mică parte din atractor, iar la , mișcarea devine periodică.

B.6. ECUAȚIA DUFFING CU DOUĂ GAURI POTENȚIALE: ATRACTOR HOLMES

Acest exemplu a fost discutat în cartea noastră. Mai multe experimente numerice merită repetate. În acest caz, ecuațiile adimensionale au forma

(Prin stabilirea și introducerea ecuației suplimentare z = w, acestea pot fi scrise ca un sistem autonom de ordinul trei.) Factorul 1/2 face ca frecvența naturală a oscilațiilor mici din fiecare puț de potențial să fie egală cu unitatea. Criteriul haosului pentru un coeficient de amortizare fix și variabile a fost considerat de noi în Cap. 5. Un domeniu de interes pentru cercetare este. În această regiune ar trebui să existe o trecere de la regimul periodic la cel haotic, ferestre periodice în regimul haotic și ieșirea din regimul haotic la . Există un alt domeniu interesant: în toate studiile, recomandăm insistent cititorului să folosească harta Poincaré. Atunci când utilizați un computer personal, procesarea informațiilor de mare viteză poate fi realizată prin trucuri speciale la crearea unui program (vezi Fig. 5.3).

Un alt experiment numeric interesant este fixarea parametrilor, de exemplu, setarea și variația fazei hărții Poincaré, adică trasarea punctelor cu variație de la 0 la Rețineți inversarea hărții la Este aceasta legată de simetria ecuației? (A se vedea figura 4.8.)

B.7. HARTĂ CUBICĂ (HOLMES)

Am ilustrat multe concepte ale teoriei oscilațiilor haotice folosind exemplul unui atractor într-un model cu două puțuri potențiale. Dinamica unui astfel de model este descrisă de o ecuație diferențială neliniară obișnuită de ordinul doi (vezi cap.

2 și 3), dar o formulă explicită pentru harta Poincaré a unui astfel de atractor este necunoscută. Holmes a propus o mapare cubică bidimensională care are unele proprietăți ale unui oscilator Duffing cu rigiditate negativă:

Un atractor haotic poate fi găsit lângă valorile parametrilor

B.8. AFIȘAREA O MINGE care sări (AFIȘARE STANDARD)

(Vezi articolul lui Holmes și cartea lui Lichtenberg și Lieberman.) După cum s-a menționat în cap. 3, harta Poincaré pentru o minge care sare pe o masă vibrantă poate fi scrisă cu precizie în termeni de viteza adimensională a mingii care lovește masa și faza de mișcare a mesei.

unde este pierderea de energie la impact.

Caz (haos conservator). Acest caz este studiat în cartea lui Lichtenberg și Lieberman ca model pentru accelerarea electronilor în câmpurile electromagnetice. După repetarea afișajului, trasați punctele rezultate pe plan. Pentru a calcula, utilizați expresia

într-o versiune îmbunătățită a BASIC. Pentru a obține o imagine bună, va trebui să variați condițiile inițiale. De exemplu, selectați și monitorizați câteva sute de iterații de mapare la v diferit de intervalul -

Veți găsi cazuri interesante când. Când se pot observa traiectorii închise cvasi-periodice în jurul punctelor fixe periodice ale cartografierii. La , regiunile de haos conservator ar trebui să apară în apropierea punctelor separatoarelor (vezi Fig. 5.21).

Caz. Acest caz corespunde unei mapări disipative, când se pierde energie la fiecare ciocnire între minge și masă. Începe cu . Rețineți că, deși primele iterații par haotice, ca în cazul 1, mișcarea devine periodică. Pentru a obține un haos asemănător fractalului, valorile K trebuie crescute la . Veți obține un atractor ciudat, care amintește și mai mult de un fractal, asumând .

B.9. AFIȘAREA CERCULUI PE DVS. SINCRONIZAREA NUMĂRULUI DE ROTIȚII ȘI A COBACI DE ZÂNE

Un punct care se deplasează de-a lungul suprafeței unui tor poate servi ca model matematic abstract al dinamicii a două oscilatoare cuplate. Amplitudinile de mișcare ale oscilatorilor servesc ca razele minore și majore ale torului și sunt adesea presupuse a fi fixe. Fazele oscilatoarelor corespund două unghiuri care specifică poziția punctului de-a lungul cercului mic (meridian) și a cercului mare (paralel) pe suprafața torusului. Secțiunea Poincaré de-a lungul cercurilor mici ale torusului generează o ecuație a diferenței unidimensionale numită harta cercului pe sine:

unde este o funcție periodică.

Fiecare iterație a acestei mapări corespunde traiectoriei unui oscilator de-a lungul cercului mare al torului. Un obiect de studiu popular este așa-numita mapare a cercului standard (normalizată la )

Posibilele mișcări observate cu această cartografiere sunt: ​​moduri periodice, cvasiperiodice și haotice. Pentru a vedea ciclurile periodice, trasați puncte pe un cerc cu coordonate dreptunghiulare

La parametrul 0 nu există nimic mai mult decât numărul de rotații - raportul a două frecvențe ale oscilatoarelor neînrudite.

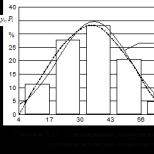
Când afișajul poate fi periodic și când este un număr irațional. În acest caz, ei spun că oscilatoarele sunt sincronizate sau că s-a produs strângerea modului. Când se pot observa mișcări sincronizate sau periodice în regiuni de lățime finită de-a lungul axei O, care, desigur, conțin valori iraționale ale parametrului. De exemplu, când un ciclu cu perioada 2 poate fi găsit în interval și un ciclu cu perioada 3 poate fi găsit în interval. Pentru a găsi aceste intervale când, calculați numărul de rotații W în funcție de parametrul la 0 01. Calculăm numărul de rotații dacă renunțăm la operația de comparare și mergem la limită

În practică, pentru a obține numărul de rotații cu suficientă precizie, trebuie să luați N > 500. Prin trasarea W versus , veți vedea o serie de platouri corespunzătoare regiunilor de sincronizare. Pentru a vedea mai multe zone de sincronizare, ar trebui să selectați o zonă mică AP și să trasați W pentru un număr mare de puncte din această zonă mică.

Fiecare platou de sincronizare de pe graficul ) corespunde unui număr rațional - raportul dintre ciclurile unui oscilator și q cicluri ale altui oscilator. Relațiile sunt aranjate într-o secvență cunoscută ca un arbore Fary. Dacă sunt date două regiuni de sincronizare de mod pentru valorile parametrilor, atunci între ele în interval va exista cu siguranță o altă regiune de sincronizare cu numărul de rotații

Începând cu 0/1 at și 1/1 at, puteți construi întreaga secvență infinită de zone de sincronizare. Cele mai multe dintre ele sunt foarte înguste.

Rețineți că lățimea acestor regiuni tinde spre zero și devine mai mare la Sincronizarea regiunilor din plan () au forma unor proeminențe lungi și sunt uneori numite limbi Arnold.

B.10. ATRACTOR RÖSSLER: REACȚII CHIMICE, APROXIMARE UNIDIMENSIONALĂ A SISTEMELOR MULTI-DIMENSIONALE

Fiecare dintre principalele domenii ale fizicii clasice și-a creat propriul model de dinamică haotică: mecanica fluidelor - ecuațiile Lorentz, mecanica structurală - atractorul Duffing-Holmes cu două puțuri potențiale, inginerie electrică - atractorul Duffing-Ueda. Un alt model simplu a apărut în dinamica reacțiilor chimice care au loc într-un recipient cu agitare. A fost sugerat de Rubssler.

unde este suma diagonalelor minore de ordinul întâi ale matricei A

– suma diagonalelor minore de ordinul doi al matricei A

– suma diagonalelor minore de ordinul al treilea al matricei A

LăsaA= - ,b= , atunci XY de ordinul 3 are forma:

Condiție:

Ф(a,b,c)<0 – все собст.знач.-я ХП вещественные

Ф(a,b,c)>

Două ecuații caracteristice ale lui Rössler.

Când rezolvați un sistem de ecuații diferențiale, există 2 puncte singulare P10(0,0,0) și P20==(c-ab,b-c/a,c/a-b), dacă faceți toate operațiile cu găsirea jacobianului și sumele elementelor diagonale, apoi se vor obține 2 ecuații Resslera:

3.3 Condiție pentru determinarea tipului de valori proprii ale unei ecuații caracteristice de ordinul trei.

Condiție:

Ф(a,b,c)=(9c-ab) 2 -(6b-2a 2)(6ac-2b 2)

Ф(a,b,c)<0 – все собст.знач.-я ХП вещественные

Ф(a,b,c)=0 – două (trei) substanțe multiple. rădăcină

Ф(a,b,c)>0 – două rădăcini complexe conjugate

Rădăcinile ecuației caracteristice cu parametri: 0,38; 0,30; 4.82 (șa de focalizare instabilă).

Curbele integrale trebuie construite relativ la fiecare punct singular.

Toate „condițiile” sunt considerate + condiția (s-av)>0 și (s-av)<0 рассматирваием для Ро1=(0,0,0)

Dacă luăm în considerare ecuațiile cu parametrii 0,38..., atunci obținem o traiectorie interesantă, traiectoria este respinsă de la Po1(0,0,0) de-a lungul R2 (x1,x2) în spațiul de fază R3 și este atrasă de-a lungul unui curbă unidimensională, formând un punct fix de tip șa -focus. Punctul reprezentativ părăsește regiunea unui punct de echilibru instabil de tip Po1 în planul variabilelor (x1,x3), apoi revine din nou în acest punct.

Traiectoria homoclinică în spațiul de fază al sistemului.

Portretul de fază face posibilă reprezentarea unei caracteristici calitative a întregului set de mișcări libere (procese) pentru o regiune selectată a spațiului rădăcină NU.

dacă traiectoria părăsește originea coordonatelor, atunci, după ce a făcut o revoluție completă în jurul unuia dintre punctele stabile, se va întoarce înapoi la punctul inițial - apar două bucle homoclinice (Conceptul de traiectorie homoclinică înseamnă că pleacă și ajunge la aceeaşi poziţie de echilibru).

Traiectoria homoclinică– nu apare dacă parametrii nu satisfac o constrângere strictă.

Instabilitatea structurală a unei traiectorii homoclinice.

La valori mari ale parametrului, traiectoria suferă modificări semnificative. Shilnikov și Kaplan au arătat că la r foarte mare sistemul intră în modul de auto-oscilație, iar dacă parametrul este redus, se va observa o tranziție către haos printr-o succesiune de dublari ale perioadei de oscilație.

Traiectorii homoclinice- instabil structural.

Atractor ciudat

Atractor ciudat: o pozitie instabila de echilibru este principala caracteristica a comportamentului haotic. Traiectoriile sunt foarte sensibile la modificările condițiilor inițiale - această calitate este inerentă atractorilor ciudați.

Un atractor ciudat este un atractor care are două diferențe semnificative față de un atractor obișnuit: traiectoria unui astfel de atractor este neperiodic (nu se închide) și modul de funcționare este instabil (mici abateri de la mod cresc). Principalul criteriu pentru natura haotică a unui atractor este creșterea exponențială în timp a micilor perturbări. Consecința acestui lucru este „amestecarea” în sistem, neperiodicitatea în timp a oricăreia dintre coordonatele sistemului, un spectru de putere continuu și o funcție de autocorelare care scade în timp.

Dinamica atractorilor ciudați este adesea haotică: prezicerea unei traiectorii care cade într-un atractor este dificilă, deoarece o mică inexactitate a datelor inițiale poate duce după un timp la o discrepanță puternică între prognoză și traiectoria reală. Imprevizibilitatea traiectoriei în sistemele dinamice deterministe se numește haos dinamic, deosebindu-l de haosul stocastic care apare în sistemele dinamice stocastice. Acest fenomen se mai numește și efectul fluturelui, implicând posibilitatea de a transforma curenții slabi de aer turbulenți cauzați de baterea aripilor unui fluture într-un punct al planetei într-o tornadă puternică pe cealaltă parte, datorită intensificării multiple a acestora în atmosferă peste un timp. perioada de timp.

Este posibil să aveți atât un comportament stocastic, cât și un comportament regulat în același timp? Sau este întotdeauna fie obișnuit, fie stocastic?

Atât comportamentul regulat, cât și cel haotic al sistemelor disipative dinamice cu multe variabile (n>2) sunt posibile, nu numai separat (fie sau), ci și simultan.

Nu se poate spune că sistemul intră în haos după prima bifurcare (deoarece a intrat într-un loc și a venit în altul)

De ce a treia comandă? Este posibil ca în sistemele de ordinul doi să apară atractori ciudați? Și în sisteme mai mari decât ordinul trei?

Condițiile matematice mai precise pentru apariția haosului arată astfel:

Sistemul trebuie să aibă caracteristici neliniare, să fie stabil la nivel global, dar să aibă cel puțin un punct de echilibru instabil de tip oscilator, iar dimensiunea sistemului trebuie să fie de cel puțin 1,5 (adică, ordinea ecuației diferențiale este de cel puțin 3).

Sistemele liniare nu sunt niciodată haotice. Pentru ca un sistem dinamic să fie haotic, trebuie să fie neliniar. Conform teoremei Poincaré-Bendixson, un sistem dinamic continuu pe un plan nu poate fi haotic. Dintre sistemele continue, numai sistemele spațiale neplate au comportament haotic (este necesară prezența a cel puțin trei dimensiuni sau geometrie non-euclidiană). Cu toate acestea, un sistem dinamic discret la un anumit stadiu poate prezenta un comportament haotic chiar și în spațiul unidimensional sau bidimensional.

Curs 3. Sisteme integrabile și neintegrabile. Sisteme conservatoare

Sisteme integrate

1. Reductibilitate la mișcarea liberă (neperturbată) a sistemelor. Ce se întâmplă dacă există ireductibilitate?

Pentru sistemele integrabile, putem elimina interacțiunile și reducem problema la problema de mișcare liberă. Pentru mișcarea liberă, nu este dificil să găsiți expresii pentru coordonatele și vitezele sub forma unor funcții explicite ale timpului. Pentru sistemele neintegrabile, este necesar să se abandoneze descrierea în termeni de traiectorii și să plece la o descriere probabilistică (cu ireductibilitate).

Este posibil să descriem un sistem neintegrabil în termeni de traiectorii?

nu imposibil. Vorbim despre o descriere fundamental probabilistică, ireductibilă la o descriere în termeni de traiectorii individuale.

Poate un sistem definit printr-o ecuație deterministă să aibă dinamică stocastică?

D. s. opus sistemului probabilistic, ale căror ieșiri depind doar aleatoriu și nu unic de intrări.(în ds depinde în mod unic de intrări).Dar orice sistem, chiar dacă este determinist, va conține o anumită aleatorie.

Articolul este dedicat utilizării metodei de proiectare analitică a controlerelor agregate pentru dezvoltarea legilor de control pentru sisteme dinamice neliniare tipice cu dinamică haotică, care asigură stabilizarea stărilor de echilibru în astfel de sisteme. Articolul prezintă o soluție la una dintre problemele caracteristice controlului antihaotic și anume problema suprimării oscilațiilor aperiodice în astfel de sisteme. Au fost dezvoltate legi de control sinergetic pentru modelele haotice Lorentz și Ressler, care asigură stabilizarea variabilelor de fază în aceste modele. Introducerea feedback-ului sintetizat duce la apariția unei stări de echilibru în sisteme. S-a realizat modelarea computerizată a sistemelor dinamice închise sintetizate, ceea ce confirmă prevederile teoretice ale teoriei controlului sinergetic. Legile de control sintetizate pot fi utilizate în diverse aplicații tehnice pentru a îmbunătăți eficiența funcționării lor.

model Lorentz

Modelul Ressler

sistem dinamic

Control

sinergetice

Părere

autooscilații

1. Anishchenko V.S., Vadivasova T.E. Prelegeri despre dinamica neliniară // Știri ale instituțiilor de învățământ superior. Dinamica neliniară aplicată. – 2010. – T. 18. – Nr. 3. – P. 186–191.

2. Kolesnikov A.A. Sinergice aplicate: fundamente ale sintezei sistemului. – Taganrog: Editura TTI SFU, 2007. – 384 p.

3. Kolesnikov A.A. Teoria managementului sinergic. – M.: Energoatomizdat, 1994. – 344 p.

4. Malinetsky G.G. Haos. Structuri. Experiment de calcul: Introducere în dinamica neliniară. – M.: Editorial URSS, 2002. – 255 p.

5. Neymark Yu.I., Landa P.S. Oscilații stocastice și haotice. – M.: Nauka, 1987. – 424 p.

6. Teoria managementului aplicat modern. Partea a II-a: Abordarea sinergetică a teoriei controlului / ed. ed. A.A. Kolesnikova. – M.-Taganrog: Editura TRTU, 2000. – 558 p.

7. Lorenz E.N. Flux neperiodic determinist // J. Atmos. Sci. – 1963. – Nr. 20. – P. 130–133.

8. Rossler O.E. O ecuație pentru haos continuu // Phys. Lett. A. – 1976. – Vol. 57A, nr 5. – P. 397–398.

Astăzi, utilizarea termenului „haos” în cercetarea științifică este asociată cu necesitatea de a descrie sisteme care sunt caracterizate de dinamică complet aleatorie, la prima vedere, și, în același timp, de prezența unei ordini ascunse în ele.

Problema științifică destul de urgentă a controlului dinamicii haotice nu a fost rezolvată în prezent. Dintre numărul mare de aspecte disponibile ale soluției sale, studiul diferitelor metode și legi care suprimă oscilațiile neregulate în sistemele neliniare, care se caracterizează prin prezența dinamicii haotice, poate fi identificat ca fiind extrem de important.

Problema controlului sistemelor neliniare cu dinamică haotică este de mare importanță practică. Este demn de remarcat faptul că punctul aici este nu numai în lupta împotriva haosului, care deseori perturbă calitatea funcționării sistemelor complexe, ci și în ideea apariției așa-numitei „ordine din haos”, care este adecvată pentru o serie de procese tehnologice.

Problema suprimării oscilațiilor neregulate este una dintre cele mai caracteristice probleme ale controlului modelelor cu dinamică haotică și constă în formarea acțiunilor de control în așa fel încât să fie asigurată stabilizarea unui model inițial haotic în stare staționară stabilă. În cele ce urmează, se presupune că este posibilă influențarea dinamicii modelului cu ajutorul unei acțiuni externe de control, care este inclusă aditiv în partea dreaptă a uneia dintre ecuațiile sale diferențiale.

Scopul studiului. În această lucrare, am rezolvat problema construirii legilor de control scalare care asigură suprimarea oscilațiilor haotice în sistemele haotice tipice ale lui Lorenz și Rössler, în care oscilațiile neregulate ale modelelor originale sunt stabilizate într-o stare stabilă de echilibru. Probleme de tip similar apar atunci când este necesară eliminarea vibrațiilor nedorite ale structurilor, diferite zgomote etc. .

Materiale și metode de cercetare

Una dintre metodele de rezolvare eficientă a problemei complexe a controlului haosului și sintetizarea legilor obiective pentru controlul sistemelor neliniare cu dinamică haotică este metoda de proiectare analitică a controlerelor agregate (ACAR), propusă de profesorul A.A. Kolesnikov.

Construcția controlerelor scalare prin metoda proiectării analitice a controlerelor agregate se bazează pe introducerea unei secvențe de varietăți invariante de dimensiune geometrică descrescătoare și descompunerea dinamică ulterioară pas cu pas a sistemului dinamic original. În acest caz, punctul reprezentativ (IT) al sistemului, începând să se deplaseze dintr-o stare inițială arbitrară, se deplasează secvenţial de la o suprafață de atracție la alta până ajunge la suprafața de finisare de forma ψ1 = 0 → ψ2 = 0 → . .. → ψm = 0. Varietățile „interne” sunt încorporate topologic în cele „externe”. Astfel, în sistemul sintetizat ia naștere un proces intern de autoguvernare. Ca urmare, are loc o formare în cascadă a unei secvențe de controale interne, care comprimă volumul de fază al sistemului în direcția de la regiunea externă a spațiului de fază la setul de regiuni interne imbricate una în cealaltă până când IT-ul atinge valoarea dorită. starea sistemului.

Să presupunem că în spațiul de stări al unui sistem închis există o varietate invariantă atrăgătoare de forma ψ(x) = 0, care este limita asimptotică a traiectoriilor de fază. În general, pot exista mai multe astfel de soiuri. De regulă, numărul de varietăți invariante coincide cu numărul de canale de control. Apoi punctul reprezentativ al sistemului începe să tindă spre intersecția varietăților invariante. O condiție necesară pentru ca punctul de reprezentare al sistemului închis „controler-obiect” să cadă pe varietatea invariantă ψ(x) = 0 este ca mișcarea sa să satisfacă o ecuație diferențială stabilă scrisă în raport cu macrovariabila agregată ψ(x). O astfel de ecuație în teoria controlului sinergetic se numește funcțională sau evolutivă. De obicei, un sistem de ecuații funcționale este specificat ca un sistem de ecuații diferențiale ordinare de ordinul întâi de forma

S = 1, 2, ..., m, Ts > 0.

Aici m este numărul de varietăți invariante date; Ts este parametrul de control, φ s (ψ s) este o funcție care trebuie să îndeplinească următorul set de condiții:

1) φ s (ψ s) trebuie să fie continuu, unic și diferențiabil pentru toate ψ-urile;

2) φ s (0) = 0;

3) φ s (ψ s ) > 0 pentru orice 0,

acestea. ele dispar numai pe varietăți φ s = 0, față de care sistemul de ecuații funcționale date este stabil asimptotic în ansamblu.

De regulă, metoda ACAR utilizează ecuații funcționale:

acestea. φ s (ψ s ) = ψ s 0. Ecuațiile de acest tip, după cum se poate observa, sunt caracterizate de stabilitate asimptotică față de varietatea ψ s = 0 în condiția Ts > 0.

În această situație, problema sintetizării legilor controlului stabilizator al modelelor haotice în cazul general se formulează astfel. Este necesar să găsim funcția uS(x) ca un anumit set de feedback-uri care asigură transferul punctului reprezentativ al modelului haotic original din condiții inițiale arbitrare dintr-o regiune admisibilă la o stare dată (mult de stări), care corespunde la un mod stabil. În cel mai simplu caz, controlul intră într-o singură ecuație diferențială a sistemului original. Pot exista opțiuni atunci când aceeași acțiune de control este localizată în linii diferite ale sistemului sursă.

Un aspect distinctiv al formulării problemei sintezei sinergice a legilor de control este prezența unei cerințe suplimentare pentru deplasarea sistemului din starea inițială în starea finală, care constă în atracția asimptotică a traiectoriilor de fază ale sistemului. la o anumită varietate invariantă (intersecția unor varietăți) în spațiul de stări (SS) al sistemului.

Introducerea feedback-ului stabilizator în ecuațiile modelului original duce la o schimbare țintită a topologiei spațiului său de stare. Ca urmare a unei astfel de restructurări, atractorul haotic dispare și se formează un atractor obișnuit de tip „punct” care corespunde modului de comportament de echilibru dorit.

Rezultatele cercetării și discuții

Să luăm în considerare etapele procedurii implementate pentru sintetizarea unei legi de control stabilizator folosind metoda AKAR pentru un sistem Lorentz haotic.

Modelul Lorentz a fost derivat inițial din Navier-Stokes și ecuațiile de conductivitate termică pentru a investiga posibilitatea de a prezice condițiile meteorologice atunci când parametrii de control variază. Modelul descrie mișcarea rolelor convective într-un lichid cu un gradient de temperatură.

Modelul reprezintă următorul sistem de trei ecuații diferențiale obișnuite:

unde σ este numărul Prandtl; ρ - număr Rayleigh normalizat; parametrul b depinde de distanța reciprocă dintre planuri și perioada orizontală.

Orez. 1. Atractor haotic al sistemului Lorentz

În acest sistem, în anumite condiții, se formează oscilații haotice. În fig. Figura 1 arată traiectoria de fază a sistemului pentru valorile parametrilor σ = 10, ρ = 24, b = 8/3 în modul haos determinist. Autooscilațiile stocastice au fost studiate pentru prima dată în acest sistem dinamic. Atractorul haotic al sistemului (1) este fundamental diferit de atractorii haotici ai majorității modelelor de dinamică neliniară. Structura sa corespunde pe deplin unui atractor ciudat și se caracterizează prin prezența doar a unui tip de mișcare de șa.

Să presupunem că acțiunea de control u1 este inclusă în prima ecuație a sistemului (1) sub formă de feedback intern:

Să introducem o varietate invariabilă a formei

unde μ este un parametru de control.

Dacă diferențiam funcția ψ1 (3) în funcție de timp și înlocuim derivata ei în ecuația funcțională

obținem legea de control dorită:

Legea de control (5) asigură transferul punctului reprezentativ al sistemului (2), închis prin feedback (5), către varietatea invariantă ψ1 = 0.

Dinamica mișcării punctului reprezentativ al modelului de-a lungul unei varietăți invariante date este descrisă folosind ecuațiile diferențiale ale modelului descompus, care se formează după înlocuirea expresiei din egalitatea ψ1 = 0 (3) în a doua și a treia ecuație. a sistemului (2):

(6)

Orez. 2. Portrete de fază ale sistemelor (2), (5) și (6)

Orez. Figura 2 ilustrează rezultatele simulării numerice a sistemului (2), (5) cu valori ale parametrilor de control σ = 10, ρ = 24, b = 8/3, caracteristice existenței unui atractor Lorentz haotic și valorile parametrilor controlerului T1 = 0,1, μ = 4, care confirmă eficacitatea prevederilor teoretice ale metodei AKAR. Prima ecuație din sistemul descompus (6) este complet identică cu ecuația evolutivă de bază a sinergeticii cu o bifurcație de tip furcă.

Să construim o lege de control stabilizator folosind metoda ACAR pentru modelul Ressler. Modelul Rössler este un sistem dinamic neliniar de ecuații diferențiale de ordinul trei de forma:

unde a, b, c sunt parametri de control.

Sistemul (7) a fost propus de Ressler pentru a modela procesele de interacțiune a unui număr de substanțe chimice. Acest sistem este destul de des folosit în diferite studii științifice ale fenomenelor de diferite naturi datorită prezenței semnelor caracteristice ale apariției și existenței dinamicii haotice. Orez. Figura 3 demonstrează atractorul haotic al sistemului Rössler cu valorile parametrilor a = b = 0,2; c = 9.

Să presupunem că acțiunea de control este inclusă în a doua ecuație a sistemului original (7):

Tip de varietate invariantă

și ecuația funcțională (4) ne permit să obținem legea de control dorită:

(10)

Legea de control (10) garantează transferul punctului reprezentativ al sistemului controlat (8), care este închis prin feedback (10), către varietatea invariantă ψ2 = 0 (9).

Orez. 3. Atractor haotic al sistemului Rössler

Natura mișcării sistemului de-a lungul varietății invariante ψ2 = 0 este descrisă de modelul descompus:

(11)

unde ecuația de bifurcație de tip furcă este prezentă în primul rând.

Orez. 4. Portrete de fază ale sistemelor (8), (10) și (11)

Orez. Figura 4 ilustrează rezultatele obținute ale simulării numerice a sistemului în buclă închisă (8), (10) pentru valorile parametrilor de control al modelului a = b = 0,2; c = 9, care sunt caracteristice apariției unui atractor de tip haotic, precum și valorile parametrilor controlerului T2 = 0,1; μ = 25.

În ambele modele descompuse obținute (6), (11), ecuațiile situate în primul rând coincid cu ecuația evolutivă de bază a sinergeticii cu o bifurcație de tip furcă. În acest sens, putem afirma natura naturală a legilor sintetizate ale controlului stabilizator al sistemelor haotice originale și unitatea existentă și interconectarea internă a ecuațiilor evolutive universale ale teoriei neliniare a auto-organizării și sinergetice.

Natura naturală a legilor de control sintetizate se datorează, în primul rând, prezenței unui set de proprietăți tipice de bifurcare în sistemele închise.

În urma studiului, a fost sintetizat un set de conexiuni de feedback, la închiderea sistemelor haotice inițiale, are loc o schimbare a naturii comportamentului acestora și are loc transformarea unui atractor de tip haotic într-un atractor de tip „punctual”. Legile de control obținute u1 (5) și u2 (10) sunt garantate pentru a oferi stabilitate asimptotică în întreg spațiul fazelor în raport cu stările de echilibru dorite la valorile parametrului μ< 0 или μ >0 pentru modelele haotice inițiale corespunzătoare. Legile obținute u1 (5) și u2 (10) aparțin clasei legilor de control obiectiv care transformă sistemele Lorentz și Ressler, care au dinamică haotică, în ecuațiile evolutive de bază ale teoriei auto-organizării și sinergetice.

Legile de control sintetizate u1 (5) și u2 (10) sunt originale și universale. Ele pot fi utilizate în proiectarea sistemelor controlate în diverse scopuri, crescând semnificativ eficiența funcționării lor.

Link bibliografic