Gamma-jakauma on matemaattinen odotus. Gamma-jakauma ja Erlang-jakauma. Luotettavuusindikaattoreiden jakaumafunktion muodostaminen tilastotietojen käsittelyn tulosten perusteella

JATKUVIEN SATUNNAISMUUTTAJIEN JAKELUA KOSKEVAT PERUSLAIT

Hnormaalijakauman laki ja sen merkitys todennäköisyysteoriassa. Logaritminen normaali laki. Gamma-jakauma. Eksponentiaalilaki ja sen käyttö luotettavuusteoriassa, jonoteoriassa. Tasa-arvoinen laki. jakelu. Opiskelijoiden jakelu. Fisherin jakelu.

1. Normaalijakauman laki (Gaussin laki).

Normaalijakautuneen satunnaismuuttujan todennäköisyystiheys ilmaistaan ​​kaavalla:

. (8.1)

Kuvassa 16 esittää jakautumiskäyrää. Se on symmetrinen noin

Riisi. 16 Kuva. 17

pisteitä (maksimipiste). Pienettäessä maksimipisteen ordinaatta kasvaa loputtomasti. Tässä tapauksessa käyrä litistetään suhteellisesti abskissa-akselia pitkin siten, että sen pinta-ala graafin alla on yhtä suuri (kuva 17).

Normaalijakauman laki on hyvin yleinen käytännön ongelmissa. Ljapunov selitti ensimmäisenä syyt normaalijakolain laajalle leviämiselle. Hän osoitti, että jos satunnaismuuttuja voidaan pitää summana suuri numero pienillä ehdoilla, sitten riittää yleiset ehdot tämän satunnaismuuttujan jakautumislaki on lähellä normaalia riippumatta siitä, mitkä yksittäisten termien jakautumislait ovat. Ja koska käytännöllisesti katsoen satunnaismuuttujat ovat useimmissa tapauksissa seurausta useista eri syistä, normaalilaki osoittautuu yleisimmäksi jakauman laiksi (katso tästä lisää luku 9). Osoitetaan normaalijakauman satunnaismuuttujan numeeriset ominaisuudet:

Siten normaalijakauman lain parametrit ja lausekkeessa (8.1) ovat odotettu arvo ja satunnaismuuttujan keskihajonnan. Kun tämä otetaan huomioon, kaava (8.1) voidaan kirjoittaa uudelleen seuraavasti:

.

Tämä kaava osoittaa, että normaalijakauman lain määräävät täysin matemaattinen odotus ja satunnaismuuttujan varianssi. Näin ollen matemaattinen odotus ja varianssi luonnehtivat täysin normaalijakauman satunnaismuuttujan. On sanomattakin selvää, että yleisessä tapauksessa, kun jakautumislain luonne on tuntematon, matemaattisen odotuksen ja varianssin tieto ei riitä määrittämään tätä jakautumislakia.

Esimerkki 1. Laske todennäköisyys, että normaalijakautuma satunnaismuuttuja täyttää epäyhtälön.

Ratkaisu. Käyttämällä todennäköisyystiheyden ominaisuutta 3 (luku 4, jakso 4) saamme:

.

,

missä on Laplace-funktio (katso liite 2).

Tehdään muutamia numeerisia laskelmia. Jos laitamme , esimerkin 1 olosuhteissa, niin

Viimeinen tulos tarkoittaa, että todennäköisyydellä lähellä yhtä () normaalijakauman lakia noudattava satunnaismuuttuja ei ylitä väliä . Tätä lausuntoa kutsutaan kolme sigma sääntöä.

Lopuksi, jos , niin normaalin lain mukaan jaettua satunnaismuuttujaa tällaisilla parametreilla kutsutaan standardoiduksi normaalimuuttujaksi. Kuvassa Kuva 18 esittää kaavion tämän arvon todennäköisyystiheydestä .

2. Logaritminen normaalijakauma.

Satunnaismuuttujan sanotaan olevan log-normaalijakauma (lyhennetty lognormaali jakauma), jos sen logaritmi on normaalijakautunut, eli jos

jossa arvolla on normaalijakauma parametrien kanssa , .

Lognormaalijakauman tiheys saadaan seuraavalla kaavalla:

, .

Matemaattinen odotus ja varianssi määritetään kaavoilla

,

.

Jakaumakäyrä on esitetty kuvassa. 19.

Log-normaalijakauma esiintyy useissa teknisissä ongelmissa. Se kertoo hiukkaskokojen jakautumisen murskaamisen aikana, alkuaineiden ja mineraalien pitoisuuksien jakautumisen magmaisissa kivissä, kalamäärän jakautumisen meressä jne. Se löytyy kaikista

ne ongelmat, joissa tarkasteltavan suuren logaritmi voidaan esittää useiden itsenäisten tasaisen pienten määrien summana:

,

eli , missä ovat itsenäisiä.

Yksinkertaisin gamma-jakauma on tiheysjakauma

Missä - siirtoparametri, - gammafunktio, ts.

(2)

Jokainen jakauma voidaan "laajentaa" skaalaussiirtoperheeksi. Jakaumafunktiolla varustetun satunnaismuuttujan tapauksessa harkitse todellakin satunnaismuuttujien perhettä , missä on skaalausparametri ja on siirtoparametri. Sitten jakelufunktio on .

Sisällyttämällä jokaisen jakauman muodon (1) tiheydellä asteikkosiirtymäperheessä, saadaan parametrisoinnissa hyväksytty gammajakaumien perhe:

Tässä - muotoparametri, - mittakaavaparametri, - siirtoparametri, gammafunktio saadaan kaavalla (2).

Kirjallisuudessa on myös muita parametrisointeja. Joten parametrin sijasta käytetään usein parametria . Joskus harkitaan kahden parametrin perhettä jättäen pois siirtoparametrin, mutta säilyttäen skaalausparametrin tai sen analogin, parametrin . Joillekin sovelletuille ongelmille (esim. teknisten laitteiden luotettavuutta tutkittaessa) tämä on perusteltua, koska aineellisista näkökohdista on luonnollista olettaa, että todennäköisyysjakauman tiheys on positiivinen positiiviset arvot argumentti ja vain heille. Tämä oletus liittyy pitkäaikaiseen keskusteluun 80-luvulla "määritetyistä luotettavuusindikaattoreista", joihin emme viivyttele.

Tietyillä parametriarvojen gamma-jakauman tapauksilla on erityiset nimet. Kohteessa , meillä on eksponentiaalinen jakauma. Luonnollisena gamma-jakauma on Erlang-jakauma, jota käytetään erityisesti jonoteoriassa. Jos satunnaismuuttujalla on gamma-jakauma ja muotoparametri on sellainen, että - kokonaisluku ja, sitten sillä on chi-neliöjakauma vapausasteilla.

Gamma-jakauman sovellukset

Gamma-jakaumalla on laajat sovellukset teknisten tieteiden eri aloilla (erityisesti luotettavuus- ja testiteoriassa), meteorologiassa, lääketieteessä ja taloustieteessä. Erityisesti tuotteen kokonaiskäyttöikä, johtavien pölyhiukkasten ketjun pituus, aika, joka kuluu tuotteen saavuttamiseen korroosion aikana rajatilaan, käyttöaika k:nneen vikaan jne. voidaan alistaa gamma-jakauma. . Kroonisia sairauksia sairastavien potilaiden elinajanodote, aika tietyn vaikutuksen saavuttamiseen hoidossa joissakin tapauksissa ovat gamma-jakaumia. Tämä jakauma osoittautui sopivimmaksi kuvaamaan kysyntää useissa varastonhallinnan taloudellisissa ja matemaattisissa malleissa.

Mahdollisuus käyttää gamma-jakaumaa useissa sovellettavissa ongelmissa voidaan joskus perustella toistettavuusominaisuuden avulla: riippumattomien eksponentiaalisesti jakautuneiden satunnaismuuttujien summalla, joilla on sama parametri, on gamma-jakauma muoto- ja mittakaavaparametreineen ja vaihtaa. Siksi gamma-jakaumaa käytetään usein sovelluksissa, joissa käytetään eksponentiaalista jakaumaa.

Satoja julkaisuja on omistettu erilaisille gamma-jakaumaan liittyville tilastoteorian aiheille (ks. yhteenvedot). Tässä artikkelissa, joka ei väitä olevan kattava, käsitellään vain joitain valtion standardin kehittämiseen liittyviä matemaattisia ja tilastollisia ongelmia.

Harkitse gamma-jakaumaa, laske sen matemaattinen odotus, varianssi, moodi. MS EXCEL GAMMA.DIST() -funktiolla piirretään jakaumafunktio ja todennäköisyystiheyskaaviot. Luodaan joukko satunnaislukuja ja arvioidaan jakautumisparametrit.

Gamma-jakauma(Englanti) Gammajakelu) riippuu 2 parametrista: r(määrittää jakauman muodon) ja λ (määrittää asteikon). tämä jakauma saadaan seuraavalla kaavalla:

missä Г(r) on gammafunktio:

jos r on positiivinen kokonaisluku, niin Г(r)=(r-1)!

Yllä oleva ilmoittautumislomake jakautumistiheys osoittaa selvästi suhteensa. Jos r = 1 Gamma-jakauma tiivistyy eksponentiaalinen jakautuminen parametrilla λ.

Jos parametri λ on kokonaisluku, niin Gamma-jakauma on summa r riippumaton ja tasaisesti jakautunut eksponentiaalinen laki satunnaismuuttujien parametrilla λ x. Siis satunnaismuuttuja y= x 1 + x 2 +… x r Sillä on gamma-jakauma parametrien kanssa r ja λ.

puolestaan ​​liittyy läheisesti diskreettiin . Jos Poisson-jakauma kuvaa satunnaisten tapahtumien määrää tietyllä aikavälillä, sitten eksponentiaalinen jakauma, tässä tapauksessa kuvaa kahden peräkkäisen tapahtuman välisen ajanjakson pituutta.

Tästä seuraa, että esimerkiksi jos ensimmäistä tapahtumaa edeltävää aikaa kuvataan eksponentiaalinen jakautuminen parametrilla λ, niin kuvataan aika, joka kuluu toiseen tapahtumaan gamma-jakauma r = 2 ja sama parametri λ.

Gamma-jakauma MS EXCELissä

MS EXCELissä käytetään vastaavaa, mutta erilaista merkintätapaa tiheys gamma-jakauma.

Parametri α ( alfa) vastaa parametria r, ja parametri b (beeta) - parametri 1/λ. Jäljempänä noudatamme juuri tällaista merkintää, koska tämä helpottaa kaavojen kirjoittamista.

MS EXCELissä, versiosta 2010 alkaen, for Jakauma Gamma on GAMMA.DIST()-funktio, Englantilainen nimi- GAMMA.JAKAUMA(), jonka avulla voit laskea todennäköisyystiheys(katso kaava yllä) ja (todennäköisyys, että satunnaismuuttuja X on gamma-jakauma, saa arvon, joka on pienempi tai yhtä suuri kuin x).

Huomautus: Ennen MS EXCEL 2010:tä EXCELissä oli GAMMADIST()-funktio, jonka avulla voit laskea integraalinen jakelufunktio Ja todennäköisyystiheys. GAMMADIST() jätetään MS EXCEL 2010:een yhteensopivuuden vuoksi.

Funktiokaaviot

Esimerkkitiedosto sisältää kaavioita todennäköisyysjakauman tiheys Ja integraalinen jakelufunktio.

Gamma-jakauma on merkintä Gamma (alfa; beeta).

Huomautus: Kaavojen kirjoittamisen helpottamiseksi jakeluparametrien esimerkkitiedostoon alfa ja beta luotu vastaava .

Huomautus: Riippuvuus 2 parametrista mahdollistaa erimuotoisten jakaumien rakentamisen, mikä laajentaa tämän jakauman soveltamista. Gamma-jakauma, Kuten Eksponentiaalinen jakautuminen käytetään usein laskemaan odotusaikaa välillä satunnaisia ​​tapahtumia. Lisäksi tätä jakoa on mahdollista käyttää sademallinnukseen ja tiesuunnitteluun.

Kuten yllä näkyy, jos parametri alfa= 1, sitten GAMMA.JAKAUMA()-funktio palauttaa parametrin 1/beta. Jos parametri beeta= 1, GAMMA.JAKAUMA()-funktio palauttaa standardin gamma-jakauma.

Huomautus: Koska on erikoistapaus gamma-jakauma, sitten kaava =GAMMA.JAKAUMA(x,n/2,2,TOSI) positiiviselle kokonaisluvulle n palauttaa saman tuloksen kuin kaava =XI2.JAKAUMA(x, n, TOSI) tai =1-XI2.JAKAUMA.X(x;n) . Ja kaava =GAMMA.JAKAUMA(x,n/2,2,EPÄTOSI) palauttaa saman tuloksen kuin kaava =XI2.JAKAUMA(x, n, EPÄTOSI), eli todennäköisyystiheys XI2-jakaumat.

SISÄÄN esimerkkitiedosto Grafiikka-arkilla laskelma annetaan gamma-jakauma yhtä suuri alfa*beta Ja

Tasainen jakelu. jatkuva arvo X on jakautunut tasaisesti väliajalla ( a, b) jos kaikki sen mahdolliset arvot ovat tällä välillä ja todennäköisyysjakauman tiheys on vakio:

Satunnaismuuttujalle X, jakautuu tasaisesti väliin ( a, b) (Kuva 4), todennäköisyys putoaa mihin tahansa väliin ( x 1 , x 2) makaa intervallin sisällä ( a, b), on yhtä suuri kuin:

(30)


Riisi. 4. Kaavio tasaisen jakautumistiheydestä

Esimerkkejä tasaisesti hajautettuja muuttujia ovat pyöristysvirheitä. Joten jos tietyn funktion kaikki taulukkoarvot pyöristetään samaan numeroon, valitse taulukkoarvo satunnaisesti, katsomme, että valitun luvun pyöristysvirhe on satunnaismuuttuja, joka on jakautunut tasaisesti väliin

eksponentiaalinen jakautuminen. Jatkuva satunnaismuuttuja X Sillä on eksponentiaalinen jakautuminen

(31)

Todennäköisyysjakauman tiheyden (31) käyrä on esitetty kuvassa. 5.

Riisi. 5. Kuvaaja eksponentiaalisen jakauman tiheydestä

Aika T tietokonejärjestelmän häiriötön toiminta on satunnaismuuttuja, jolla on eksponentiaalinen jakauma parametrin kanssa λ , fyysinen merkitys joka on keskimääräinen vikojen lukumäärä aikayksikköä kohden, pois lukien järjestelmän korjausseisokit.

Normaali (Gaussin) jakauma. Satunnainen arvo X Sillä on normaali (gaussinen) jakauma, jos sen todennäköisyyksien tiheysjakauma määräytyy riippuvuudella:

(32)

Missä m = M(X) , .

klo kutsutaan normaalijakaumaa standardi.

Normaalijakauman (32) tiheyden käyrä on esitetty kuvassa. 6.

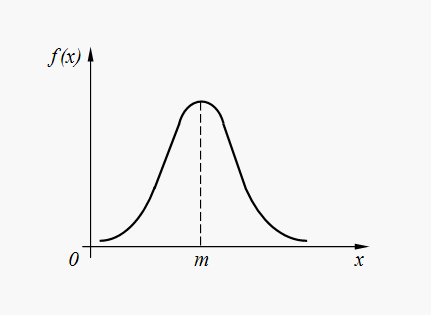
Riisi. 6. Kuvaaja normaalijakauman tiheydestä

Normaalijakauma on yleisin jakauma erilaisissa luonnon satunnaisissa ilmiöissä. Joten virheet automatisoidun laitteen komentojen suorittamisessa, tulostusvirheet avaruusalus tiettyyn pisteeseen avaruudessa, tietokonejärjestelmien parametrien virheet jne. useimmissa tapauksissa jakauma on normaali tai lähellä normaalia. Lisäksi summauksen muodostamat satunnaismuuttujat suuri numero satunnaiset termit jakautuvat lähes normaalin lain mukaan.

Gamma-jakauma. Satunnainen arvo X Sillä on gamma-jakauma, jos sen todennäköisyyksien tiheysjakauma ilmaistaan ​​kaavalla:

(33)

Missä on Eulerin gammafunktio.

GAMMAJAKUN SOVELTAMISKÄYTÄNTÖ TEKNISTEN JÄRJESTELMIEN LUOTETTAVUUSTEORIA

Ruslan Litvinenko

teknisten tieteiden kandidaatti, apulaisprofessori sähköteknisten kompleksien ja järjestelmien alaosastolla, Kazanin osavaltion sähkötekniikan yliopisto,

Venäjä,Tatarstanin tasavalta,Kazan

Aleksandr Jamshhikov

mestari opiskelija,

Venäjä,Tatarstanin tasavalta,Kazan

Aleksej Bagaev

mestari opiskelijaKazanin osavaltion sähkötekniikan yliopisto,

Venäjä,Tatarstanin tasavalta,Kazan

HUOMAUTUS

Käytännössä teknisten järjestelmien käytössä useimmiten joudutaan käsittelemään todennäköisyyspohjaisia ​​(satunnaisia) prosesseja, kun funktio heijastaa argumenttia tietyllä todennäköisyydellä. Pienistä tilastotietomääristä johtuvien vikojen esiintymisajan jakautumislain informaation epävarmuuden olosuhteissa, mikä yleensä tapahtuu alkuvaiheessa tekniikan kehityksen myötä tutkijan on tehtävä päätös a priori luotettavuusmallin valinnasta prototyyppien tai analogien aikaisemman käytön kokemuksen perusteella. Tiedon systematisointi perusjakaumien käytännön käytöstä erilaisten teknisten järjestelmien luotettavuuden ennustamisessa ja arvioinnissa on kiireellinen tieteellinen tehtävä.

Esitetty materiaali perustuu kirjallisuudessa julkaistun tiedon systematisointiin ja edustaa malli- ja tutkimustulosten analysointia. kokeelliset tutkimukset laitteiden luotettavuus sekä käytön aikana saadut tilastotiedot.

Esitettyä teoreettista tietoa gamma-jakauman käytöstä luotettavuusteoriassa voidaan käyttää ensimmäisenä likiarvona, ja sitä on tarkennettava eri hypoteesien testauskriteereillä, koska tilastotietojen määrä kasvaa myöhempien testien aikana.

On oltava tarpeeksi syitä soveltaa eksponentiaalista jakautumislakia, kuten kaikkia muitakin. Tästä syystä artikkeli voi olla hyödyllinen teknisen järjestelmän kehitys- tai modernisoinnin alkuvaiheessa oleville tutkijoille a priori tietona rakennusmalleista ja luotettavuuden varmistamiseen ja valvontaan käytettävistä kriteereistä.

ABSTRAKTI

Käytännössä teknisten järjestelmien toiminta joutuu useimmiten käsittelemään stokastisia (satunnaisia) prosesseja, kun funktio heijastaa argumenttia tietyllä todennäköisyydellä. Pienistä tilastotietomääristä johtuvien vikojen esiintymisajan jakautumislain epävarmuuden edessä, mikä yleensä tapahtuu teknologian kehityksen alkuvaiheissa, tutkijan on päätettävä aikaisemman mallin luotettavuuden valinnasta aikaisempien tietojen perusteella. kokemusta prototyyppien tai analogien käytöstä. Tietojen systematisointi perusjakaumien käytännön käytöstä erilaisten teknisten järjestelmien ennustamisessa ja luotettavuuden arvioinnissa on tärkeä tieteellinen tehtävä.

Yllä olevassa aineistossa on systematisointi kirjallisuudessa julkaistuista tiedoista, jotka edustavat laitteiden luotettavuuden malli- ja kokeellisten tutkimusten analyysituloksia sekä käytön aikana saatuja tilastotietoja.

Esittää teoreettista tietoa gamma-jakauman käytöstä luotettavuusteoriassa, jota voidaan käyttää ensimmäisenä likiarvona ja se on pakollisen erittelyn alainen, käyttämällä erilaisia ​​hypoteesien testauskriteereitä, mikä lisää tilastotietojen määrää myöhemmissä testeissä.

Eksponenttijakauman lain soveltamiselle on oltava riittävä peruste, kuten minkä tahansa muunkin. Tästä syystä artikkeli voi olla hyödyllinen teknisten järjestelmien kehittämisen tai modernisoinnin alkuvaiheessa oleville tutkijoille a priori tietona luotettavuuden varmistamiseen ja valvontaan käytettävien mallien ja kriteerien rakentamiseen.

Avainsanat: luotettavuus, jakautuminen, toiminta-aika, todennäköisyys, tiheys, vaihe, matemaattinen odotus.

avainsanat: luotettavuus, jakautuminen, toiminta-aika, todennäköisyys, jakautumistiheys, vaihe, odotusarvo.

Järjestelmävikojen kuvaamiseksi voidaan ehdottaa malleja niiden ratkaisemiseksi erilaisia ​​tehtäviä luotettavuutta ja ottavat huomioon vikojen luonteeseen luontaiset tekijät eri tavoin.

Vikojen esiintymisen satunnaisuus teknisten järjestelmien ja niiden elementtien toiminnan aikana mahdollistaa todennäköisyys-tilastollisten menetelmien soveltamisen niiden kuvauksessa. Yleisimmät ovat vikamallit, jotka perustuvat vastaavien satunnaismuuttujien jakaumaan - ei-palauttavien kohteiden vikaantumisaika ja palautettavien kohteiden vikojen välinen aika.

Tuotteiden toiminta-ajan pääasiallisina jakautumistyypeinä vikaantumiseen on tarpeen erottaa:

• eksponentiaalinen;
• Weibulla-Gnedenko;
• gamma;
• log-normaali;
• normaali.

Teknisten järjestelmien luotettavuuden alan kirjallisuuden katsauksen tuloksena tehtiin arvio gamma-jakauman käytännön soveltamisesta erilaisten teknisten kohteiden tutkimuksessa. Tehdyn analyysin perusteella on mahdollista valita sopiva ennakkojakauma vastaavalle kriteerille tai luotettavuusindikaattorille.

Gamma-jakaumalla on kahden parametrin tiheys muotoparametrilla ja skaalausparametrilla:

.

Virheettömän toiminnan todennäköisyys määritetään kaavalla:

,

Missä: on gammafunktio;

on epätäydellinen gammafunktio.

Gamma-jakauman matemaattinen odotus (keskimääräinen aika vikojen välillä) ja standardipoikkeama ovat:

.

Vikasuhteen kaava on seuraava:

.

Gamma-jakauma kuvaa kulumishäiriöitä; vauriot, jotka johtuvat vaurioiden kertymisestä; kuvaukset monimutkaisen teknisen järjestelmän käyttöajasta, jossa on redundantteja elementtejä; toipumisajan jakaumat; ja sitä voidaan käyttää myös joidenkin teknisten esineiden kestävyyttä (resurssia) harkittaessa.

Gamma-jakaumalla on useita hyödyllisiä ominaisuuksia:

Edellä olevan perusteella voidaan päätellä, että gamma-jakaumaa voidaan käyttää kaikilla elinkaaren alueilla: sisäänajossa (), normaalikäytössä () ja ikääntymisessä () .

Perustuen ongelmiin, jotka ratkaistaan ​​Laplace-muunnoksen avulla, on kätevää käyttää gamma-jakaumaa todellisten jakaumien lähentämiseen.

B tarjoaa seuraavan määritelmän: gamma-jakauma on ominaisuus vikojen esiintymisajalle monimutkaisissa sähkömekaanisissa järjestelmissä tapauksissa, joissa elementtien välittömiä vikoja tapahtuu toiminnan alkuvaiheessa tai järjestelmän virheenkorjausprosessissa, eli se on kätevä ominaisuus laitteiden vikojen esiintymisajankohdasta sen sisäänajon aikana.

Monimutkaisissa teknisissä järjestelmissä, jotka koostuvat elementeistä, joiden virheettömän toiminnan todennäköisyydellä on eksponentiaalinen jakauma, koko järjestelmän virheettömän toiminnan todennäköisyydellä on gamma-jakauma.

Monimutkaisen teknisen järjestelmän vikojen esiintymisajan jakauma korvausreservillä (olettaen, että pääjärjestelmän ja kaikkien vara-alkueläinten vikavirrat) voidaan kuvata myös gamma-jakaumalla. Samoin kuormittamattoman tai sekavähennyksen tapauksessa järjestelmän käytettävyyden todennäköisyys noudattaa yleistä gamma-jakaumaa.

Yhteenvetona on huomattava, että yksittäisiä ongelmia ratkaistaessa käytetään myös erikoistyyppejä (niitä on useita kymmeniä) sekä diskreettejä jakaumia, joita ei otettu huomioon tämän artikkelin puitteissa. Tässä tapauksessa jakaumien välillä on erilaisia ​​keskinäisiä siirtymiä ja yhteyksiä. Huolimatta olemassa olevista kriteereistä valitun teoreettisen ja empiirisen jakauman välillä, ne kaikki antavat vastauksen kysymykseen: onko tai ei ole tarpeeksi hyviä syitä hylätä hypoteesi valitusta jakaumasta? Kirjoittajat totesivat, että mitä tahansa dataa voidaan säätää moniparametriseksi laiksi, vaikka se ei vastaisikaan todellista. fyysisiä ilmiöitä. Jakauman tyyppiä ja sen parametreja valittaessa on siis ensisijaisesti otettava huomioon meneillään olevien prosessien ja tapahtumien fyysinen luonne.

Bibliografia:

1. GOST R.27.001-2009. Luotettavuus tekniikassa. epäonnistuneet mallit. – M.: Standartinform, 2010. – 16 s.
2. Gertsbakh I.B., Kordonsky H.B. Vikamallit / toim. B.V. Gnedenko. - M.: Neuvostoliiton radio, 1966. - 166 s.
3. Gnedenko B.V. Matemaattisen luotettavuusteorian kysymyksiä. - M .: Radio ja viestintä, 1983. – 376 s.
4. Kashtanov V.N., Medvedev A.I. Monimutkaisten järjestelmien luotettavuusteoria: oppikirja - M.: FIZMATLIT, 2010. - 609 s.
5. Litvinenko R.S. Sähkökompleksin toimintaprosessin simulaatiomalli, jossa otetaan huomioon sen elementtien luotettavuus // Journal "Nadezhnost". - 2016. - nro 1 (56) - s. 46–54.
6. Litvinenko R.S., Idiyatullin R.G., Kisneeva L.N. Arvio hybridiauton luotettavuudesta kehitysvaiheessa // Lehti "Transport: science, technology, management". - 2016. - nro 2 - s. 34–40.
7. Tekniikka: 40 osan tietosanakirja T. IV-3: Koneiden luotettavuus / V.V. Klyuev, V.V. Bolotin, F.R. Sosnin ja muut; alle yhteensä toim. V.V. Klyuev. – M.: Mashinostroenie, 2003. – 592 s.
8. Trukhanov V.M. Teknisten järjestelmien, kuten liikkuvien asennusten luotettavuus prototyyppien suunnittelu- ja testausvaiheessa: tieteellinen julkaisu - M.: Mashinostroenie, 2003. - 320 s.
9. Khazov B.F., Didusev B.A. Käsikirja koneiden luotettavuuden laskemiseen suunnitteluvaiheessa. – M.: Mashinostroenie, 1986. – 224 s.
10. Cherkesov G.N. Laitteisto- ja ohjelmistojärjestelmien luotettavuus: oppikirja. korvaus. - Pietari: Pietari, 2005. - 479 s.