Lecție extracurriculară - cerc de numere. Cercul numeric Definiția sfertului de cerc

>> Cercul numeric

În timp ce studiam cursul de algebră pentru clasele 7-9, ne-am ocupat până acum de funcții algebrice, adică. funcții definite analitic prin expresii în care s-au folosit operații algebrice pe numere și variabile (adunare, scădere, înmulțire, Divizia, exponentiație, rădăcină pătrată). Dar modelele matematice ale situațiilor reale sunt adesea asociate cu funcții de alt tip, nu algebrice. Ne vom familiariza cu primii reprezentanți ai clasei de funcții non-algebrice - funcții trigonometrice - în acest capitol. Vei studia mai detaliat funcțiile trigonometrice și alte tipuri de funcții non-algebrice (exponențiale și logaritmice) în liceu.
Pentru a introduce funcții trigonometrice avem nevoie de un nou model matematic- un cerc numeric pe care nu l-ai întâlnit încă, dar ești foarte familiarizat cu linia numerică. Amintiți-vă că linia numerică este o dreaptă pe care sunt date punctul de plecare O, scara (segmentul unitar) și direcția pozitivă. Putem compara orice număr real cu un punct pe o dreaptă și invers.

Cum să găsiți punctul corespunzător M pe o dreaptă folosind numărul x? Numărul 0 corespunde punctului de pornire O. Dacă x > 0, atunci, deplasându-vă de-a lungul unei linii drepte din punctul 0 în direcția pozitivă, trebuie să mergeți n^-a din lungimea x; capătul acestei căi va fi punctul dorit M(x). Dacă x< 0, то, двигаясь по прямой из точки О в отрицательном направлении, нужно пройти путь 1*1; конец этого пути и будет искомой точкой М(х). Число х - координата точки М.

Și cum am rezolvat problema inversă, adică Cum ați găsit coordonatele x a unui punct dat M pe dreapta numerică? Am găsit lungimea segmentului OM și am luat-o cu semnul „+” sau * - „în funcție de ce parte a punctului O se află punctul M pe linie dreaptă.

Dar în viața reală trebuie să te miști nu numai în linie dreaptă. Destul de des, mișcare de-a lungul cerc. Iată un exemplu concret. Să considerăm că pista de alergare a stadionului este un cerc (de fapt, nu este, desigur, un cerc, dar nu uitați, așa cum spun de obicei comentatorii sportivi: „alergătorul a alergat un cerc”, „a mai rămas o jumătate de cerc a alerga înainte de sosire”, etc.), lungimea acestuia este de 400 m. Startul este marcat - punctul A (Fig. 97). Alerătorul din punctul A se deplasează în jurul cercului în sens invers acelor de ceasornic. Unde va fi la 200 m? la 400 m? la 800 m? la 1500 m? Unde ar trebui să tragă linia de sosire dacă parcurge o distanță de maraton de 42 km 195 m?

După 200 m, el se va afla în punctul C, diametral opus punctului A (200 m este lungimea jumătate a benzii de alergare, adică lungimea unei jumătăți de cerc). După ce a alergat 400 m (adică, „o tură”, după cum spun sportivii), se va întoarce la punctul A. După ce a alergat 800 m (adică, „două ture”), va fi din nou în punctul A. Ce înseamnă 1500 m ? Acesta este „trei cercuri” (1200 m) plus încă 300 m, adică 3

Banda de alergare - sfârșitul acestei distanțe va fi în punctul 2) (Fig. 97).

Trebuie doar să ne ocupăm de maraton. După ce a parcurs 105 ture, sportivul va parcurge o distanță de 105-400 = 42.000 m, adică. 42 km. Au mai rămas 195 m până la linia de sosire, adică cu 5 m mai puțin decât jumătate din circumferință. Aceasta înseamnă că sfârșitul distanței de maraton va fi în punctul M, situat lângă punctul C (Fig. 97).

Cometariu. Desigur, înțelegeți convenția ultimului exemplu. Nimeni nu alerga o distanta de maraton in jurul stadionului, maximul este de 10.000 m, i.e. 25 de ture.

Puteți alerga sau merge pe orice lungime de-a lungul benzii de alergare a stadionului. Aceasta înseamnă că orice număr pozitiv corespunde unui punct - „finalul distanței”. Mai mult, este posibil să atribuiți un punct pe un cerc oricărui număr negativ: trebuie doar să faceți sportivul să alerge în direcția opusă, adică. începeți din punctul A nu în sens invers acelor de ceasornic, ci în sensul acelor de ceasornic. Apoi pista de alergare a stadionului poate fi considerată ca un cerc numeric.

În principiu, orice cerc poate fi considerat un cerc numeric, dar în matematică s-a convenit să se utilizeze un cerc unitar în acest scop - un cerc cu o rază de 1. Aceasta va fi „banda de alergare” noastră. Lungimea b a unui cerc cu raza K se calculează cu formula Lungimea unui semicerc este n, iar lungimea unui sfert de cerc este AB, BC, SB, DA din Fig. 98 - egal Să fim de acord să numim arc AB primul sfert al cercului unitar, arc BC al doilea sfert, arc CB al treilea sfert, arc DA al patrulea sfert (Fig. 98). În acest caz, vorbim de obicei despre un arc deschis, adică. despre un arc fără capete (ceva ca un interval pe o dreaptă numerică).

Definiție. Este dat un cerc unitar, iar punctul de plecare A este marcat pe acesta - capătul drept al diametrului orizontal (Fig. 98). Să asociem fiecare număr real I cu un punct de pe cerc conform următoarei reguli:

1) dacă x > 0, atunci, deplasându-ne din punctul A în sens invers acelor de ceasornic (direcția pozitivă de deplasare în jurul cercului), vom descrie o cale de-a lungul cercului cu lungime și punctul final M al acestei căi va fi cel dorit punct: M = M(x);

2) dacă x< 0, то, двигаясь из точки А в направлении по часовой стрелке (отрицательное направление обхода окружности), опишем по окружности путь длиной и |; конечная точка М этого пути и будет искомой точкой: М = М(1);

Să asociem punctul A cu 0: A = A(0).

Un cerc unitar cu o corespondență stabilită (între numere reale și puncte de pe cerc) va fi numit cerc numeric.
Exemplul 1. Găsiți pe cercul numeric
Deoarece primele șase dintre cele șapte numere date sunt pozitive, atunci pentru a găsi punctele corespunzătoare pe cerc, trebuie să parcurgeți o cale de o anumită lungime de-a lungul cercului, deplasându-se din punctul A în direcția pozitivă. Să luăm în considerare asta

Numărul 2 corespunde punctului A, deoarece, după ce a trecut de-a lungul cercului, o cale de lungime 2, adică. exact un cerc, vom ajunge din nou la punctul de plecare A Deci, A = A(2).
Ce s-a întâmplat Aceasta înseamnă că, deplasându-vă din punctul A într-o direcție pozitivă, trebuie să treceți printr-un cerc întreg.

Cometariu. Când suntem în clasele a VII-a și a VIII-a a lucrat cu linia numerică, apoi am convenit, de dragul conciziei, să nu spunem „punctul de pe dreapta corespunzător numărului x”, ci să spunem „punctul x”. Vom respecta exact același acord atunci când lucrăm cu cercul numeric: „punctul f” - aceasta înseamnă că vorbim despre un punct din cerc care corespunde numărului
Exemplul 2.
Împărțind primul trimestru AB în trei părți egale prin punctele K și P, obținem:

Exemplul 3. Găsiți puncte pe cercul numeric care corespund numerelor
Vom realiza construcții folosind Fig. 99. Depunând arcul AM (lungimea lui este -) din punctul A de cinci ori în direcția negativă, obținem punctul!, - mijlocul arcului BC. Asa de,

Cometariu. Observați câteva dintre libertățile pe care le luăm în utilizarea limbajului matematic. Este clar că arcul AK și lungimea arcului AK sunt lucruri diferite (primul concept este o figură geometrică, iar al doilea concept este un număr). Dar ambele sunt desemnate la fel: AK. Mai mult, dacă punctele A și K sunt conectate printr-un segment, atunci atât segmentul rezultat, cât și lungimea acestuia sunt notate în același mod: AK. De obicei, din context, este clar ce semnificație are denumirea (arc, lungime a arcului, lungime a segmentului sau a segmentului).

Prin urmare, modelele de cerc cu două numere ne vor fi foarte utile.

PRIMUL AZAR
Fiecare dintre cele patru sferturi ale cercului numeric este împărțit în două părți egale, iar lângă fiecare dintre cele opt puncte disponibile sunt scrise „numele” lor (Fig. 100).

A DOUA DISPOZIRE Fiecare dintre cele patru sferturi ale cercului numeric este împărțit în trei părți egale, iar lângă fiecare dintre cele douăsprezece puncte disponibile sunt scrise „numele” lor (Fig. 101).

Vă rugăm să rețineți că pe ambele modele am putea atribui alte „nume” punctelor date.
Ați observat că în toate exemplele analizate de lungimi de arc
exprimată prin unele fracții ale numărului n? Acest lucru nu este surprinzător: la urma urmei, lungimea unui cerc unitar este 2n, iar dacă împărțim un cerc sau un sfert al acestuia în părți egale, obținem arce ale căror lungimi sunt exprimate în fracțiuni din numărul și. Credeți că este posibil să găsiți un punct E pe cercul unitar astfel încât lungimea arcului AE să fie egală cu 1? Să ne dăm seama:

Raționând în mod similar, concluzionăm că pe cercul unitar se poate găsi punctul Eg, pentru care AE = 1, și punctul E2, pentru care AEr = 2, și punctul E3, pentru care AE3 = 3, și punctul E4, pt. care AE4 = 4, și punctul Eb, pentru care AEb = 5, și punctul E6, pentru care AE6 = 6. În fig. 102 punctele corespunzătoare sunt marcate (aproximativ) (pentru orientare, fiecare dintre sferturile cercului unitar este împărțit prin liniuțe în trei părți egale).

Exemplul 4. Găsiți punctul de pe cercul numeric corespunzător numărului -7.

Avem nevoie, pornind de la punctul A(0) și deplasându-ne în sens negativ (sensul acelor de ceasornic), să mergem de-a lungul unui cerc de lungimea 7. Dacă trecem printr-un cerc, obținem (aproximativ) 6,28, ceea ce înseamnă că mai trebuie să parcurgeți (în aceeași direcție) o cale de lungime 0,72. Ce fel de arc este acesta? Puțin mai puțin de jumătate de sfert de cerc, adică. lungimea sa este mai mică decât numărul -.

Deci, pe un cerc numeric, ca pe o dreaptă numerică, fiecărui număr real îi corespunde un punct (numai că, desigur, este mai ușor să-l găsești pe o linie decât pe un cerc). Dar pentru o linie dreaptă este adevărat și opusul: fiecărui punct îi corespunde un singur număr. Pentru un cerc numeric, o astfel de afirmație nu este adevărată; am văzut în mod repetat acest lucru mai sus. Următoarea afirmație este adevărată pentru cercul numeric.
Dacă punctul M al cercului numeric corespunde numărului I, atunci îi corespunde și un număr de forma I + 2k, unde k este orice număr întreg (k e 2).

De fapt, 2n este lungimea cercului numeric (unitate) și întregul |th| poate fi considerat ca fiind numărul de runde complete ale cercului într-o direcție sau alta. Dacă, de exemplu, k = 3, atunci aceasta înseamnă că facem trei runde ale cercului în direcția pozitivă; dacă k = -7, atunci aceasta înseamnă că facem șapte (| k | = | -71 = 7) runde ale cercului în direcția negativă. Dar dacă ne aflăm în punctul M(1), atunci, după ce am efectuat și | la | cercuri complete în jurul cercului, ne vom găsi din nou în punctul M.

A.G. Mordkovich Algebra clasa a X-a

Dacă ești deja familiarizat cu cerc trigonometric , și doriți doar să vă reîmprospătați memoria cu anumite elemente, sau sunteți complet nerăbdător, atunci iată-l:

Aici vom analiza totul în detaliu pas cu pas.

Cercul trigonometric nu este un lux, ci o necesitate

Trigonometrie Mulți oameni îl asociază cu un desiș impenetrabil. Dintr-o dată, atâtea valori ale funcțiilor trigonometrice, atâtea formule se îngrămădesc... Dar parcă nu a funcționat la început și... să plecăm... neînțelegere completă...

Este foarte important să nu renunți valorile funcțiilor trigonometrice, - se spune, poți oricând să te uiți la pinten cu un tabel de valori.

Dacă te uiți constant la un tabel cu valorile formulelor trigonometrice, hai să scăpăm de acest obicei!

El ne va ajuta! Veți lucra cu el de mai multe ori și apoi vă va apărea în cap. Cum este mai bine decât o masă? Da, în tabel veți găsi un număr limitat de valori, dar pe cerc - TOTUL!

De exemplu, spune în timp ce te uiți la tabel standard de valori ale formulelor trigonometrice , care este sinusul egal cu, să zicem, 300 de grade sau -45.

În niciun caz?... poți, desigur, să te conectezi formule de reducere... Și uitându-te la cercul trigonometric, poți răspunde cu ușurință la astfel de întrebări. Și în curând vei ști cum!

Și atunci când rezolvați ecuații trigonometrice și inegalități fără un cerc trigonometric, nu este absolut nicăieri.

Introducere în cercul trigonometric

Să mergem în ordine.

Mai întâi, să scriem această serie de numere:

Si acum asta:

Și în sfârșit acesta:

Desigur, este clar că, de fapt, pe primul loc este , pe locul doi este , iar pe ultimul loc este . Adică vom fi mai interesați de lanț.

Dar ce frumos a iesit! Dacă se întâmplă ceva, vom restabili această „scara miracolă”.

Și de ce avem nevoie de ea?

Acest lanț este principalele valori ale sinusului și cosinusului în primul trimestru.

Să desenăm un cerc cu raza unitară într-un sistem de coordonate dreptunghiular (adică luăm orice rază în lungime și declarăm lungimea sa unitate).

Din fasciculul „0-Start” așezăm colțurile în direcția săgeții (vezi figura).

Obținem punctele corespunzătoare pe cerc. Deci, dacă proiectăm punctele pe fiecare dintre axe, atunci vom obține exact valorile din lanțul de mai sus.

De ce este asta, te întrebi?

Să nu analizăm totul. Sa luam in considerare principiu, care vă va permite să faceți față altor situații similare.

Triunghiul AOB este dreptunghiular și conține . Și știm că vizavi de unghiul b se află un catet de jumătate din dimensiunea ipotenuzei (avem ipotenuza = raza cercului, adică 1).

Aceasta înseamnă AB= (și prin urmare OM=). Și conform teoremei lui Pitagora

Sper că deja ceva devine clar?

Deci punctul B va corespunde valorii, iar punctul M va corespunde valorii

La fel cu celelalte valori ale primului trimestru.

După cum înțelegeți, axa familiară (bou) va fi axa cosinusului, iar axa (oy) – axa sinusurilor . Mai tarziu.

La stânga lui zero de-a lungul axei cosinus (sub zero de-a lungul axei sinusului) vor fi, desigur, valori negative.

Așadar, iată-l pe Atotputernicul, fără de care nu există nicăieri în trigonometrie.

Dar vom vorbi despre cum să folosiți cercul trigonometric.

Lecțiile video sunt printre cele mai eficiente instrumente de predare, în special la disciplinele școlare precum matematica. Prin urmare, autorul acestui material a adunat doar informații utile, importante și competente într-un singur întreg.

Această lecție durează 11:52 minute. Este nevoie de aproape aceeași cantitate de timp pentru ca un profesor să explice material nou pe o anumită temă în clasă. Deși principalul avantaj al lecției video va fi faptul că elevii vor asculta cu atenție despre ce vorbește autorul, fără a fi distrași de subiecte și conversații străine. La urma urmei, dacă elevii nu ascultă cu atenție, vor rata un punct important al lecției. Și dacă profesorul explică el însuși materialul, atunci elevii săi își pot distrage cu ușurință atenția de la lucrul principal cu conversațiile lor pe subiecte abstracte. Și, desigur, devine clar care metodă va fi mai rațională.

Autorul consacră începutul lecției repetării acelor funcții cu care elevii erau familiarizați mai devreme în cursul de algebră. Iar primele care încep să studieze sunt funcțiile trigonometrice. Pentru a le lua în considerare și a le studia, este necesar un nou model matematic. Și acest model devine cercul numeric, care este exact ceea ce este afirmat în subiectul lecției. Pentru a face acest lucru, este introdus conceptul de cerc unitar și este dată definiția acestuia. Mai departe în figură, autorul arată toate componentele unui astfel de cerc și ceea ce va fi util studenților pentru învățare ulterioară. Arcurile indică sferturi.

Apoi autorul sugerează să luăm în considerare cercul numeric. Aici el face observația că este mai convenabil să folosești un cerc unitar. Acest cerc arată cum se obține punctul M dacă t>0, t<0 или t=0. После этого вводится понятие самой числовой окружности.

În continuare, autorul le reamintește elevilor cum să găsească circumferința unui cerc. Și apoi emite lungimea cercului unitar. Se propune aplicarea acestor date teoretice în practică. Pentru a face acest lucru, luați în considerare un exemplu în care trebuie să găsiți un punct pe un cerc care să corespundă anumitor valori numerice. Soluția exemplului este însoțită de o ilustrare sub formă de imagine, precum și de notațiile matematice necesare.

Conform condiției celui de-al doilea exemplu, este necesar să se găsească puncte pe cercul numeric. Și aici, întreaga soluție este însoțită de comentarii, ilustrații și notații matematice. Acest lucru contribuie la dezvoltarea și îmbunătățirea alfabetizării matematice a elevilor. Al treilea exemplu este construit în mod similar.

În continuare, autorul notează acele numere pe cerc care apar mai des decât altele. Aici el sugerează realizarea a două modele ale unui cerc numeric. Când ambele modele sunt gata, se ia în considerare următorul, al patrulea exemplu, în care trebuie să găsiți un punct pe cercul numeric corespunzător numărului 1. După acest exemplu, se formulează o declarație conform căreia puteți găsi punctul M corespunzător numărul t.

În continuare, este introdusă o remarcă conform căreia elevii învață că numărul „pi” corespunde tuturor numerelor care se încadrează într-un punct dat atunci când trece de întregul cerc. Aceste informații sunt susținute de cel de-al cincilea exemplu. Soluția sa conține raționamente corecte din punct de vedere logic și desene care ilustrează situația.

DECODIFICAREA TEXTULUI:

CERCUL NUMERIC

Anterior, am studiat funcțiile definite prin expresii analitice. Și aceste funcții au fost numite algebrice. Dar la cursul de matematică școlară se studiază funcțiile altor clase, nu cele algebrice. Să începem să învățăm funcțiile trigonometrice.

Pentru a introduce funcții trigonometrice, avem nevoie de un nou model matematic - cercul numeric. Să luăm în considerare cercul unității. Un cerc a cărui rază este egală cu segmentul de scară, fără a indica anumite unități de măsură, va fi numit unitate. Raza unui astfel de cerc este considerată egală cu 1.

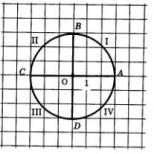
Vom folosi un cerc unitar în care sunt desenate diametrele orizontale și verticale CA și DB (ce a și de be) (vezi Figura 1).

Vom numi arc AB primul sfert, arc BC al doilea trimestru, arc CD al treilea trimestru și arc DA al patrulea trimestru.

Luați în considerare cercul numeric. În general, orice cerc poate fi considerat ca un cerc numeric, dar este mai convenabil să folosiți cercul unitar în acest scop.

DEFINIȚIE Se dă un cerc unitar, iar pe el este marcat punctul de plecare A - capătul drept al diametrului orizontal. Să asociem fiecare număr real t (te) cu un punct de pe cerc conform următoarei reguli:

1) Dacă t>0 (te este mai mare decât zero), atunci, deplasându-ne din punctul A în sens invers acelor de ceasornic (direcția pozitivă a cercului), descriem o cale AM ​​(a em) de lungime t de-a lungul cercului. Punctul M va fi punctul dorit M(t) (em din te).

2) Dacă t<0(тэ меньше нуля), то, двигаясь из точки А в направлении по часовой стрелке (отрицательное направление обхода окружности), опишем по окружности путь АМ (а эм) длины |t| (модуль тэ). Точка М и будет искомой точкой М(t) (эм от тэ).

3) Să atribuim punctul A numărului t = 0.

Un cerc unitar cu o corespondență stabilită (între numere reale și puncte de pe cerc) va fi numit cerc numeric.

Se știe că circumferința L (el) se calculează prin formula L = 2πR (el este egal cu doi pi er), unde π≈3,14, R este raza cercului. Pentru un cerc unitar R=1cm, înseamnă L=2π≈6,28 cm (el este egal cu doi pi aproximativ 6,28).

Să ne uităm la exemple.

EXEMPLU 1. Găsiți un punct pe cercul numeric care corespunde numărului dat: ,.(pi cu doi, pi, trei pi cu doi, doi pi, unsprezece pi cu doi, șapte pi, minus cinci pi cu doi)

Soluţie. Primele șase numere sunt pozitive, prin urmare, pentru a găsi punctele corespunzătoare pe cerc, trebuie să parcurgeți o cale de o anumită lungime de-a lungul cercului, deplasându-vă din punctul A în direcția pozitivă. Lungimea fiecărui sfert de cerc unitar este egală. Aceasta înseamnă că AB =, adică punctul B corespunde numărului (vezi Fig. 1). AC = , adică punctul C corespunde numărului. AD = , adică punctul D corespunde numărului. Și punctul A corespunde din nou numărului, pentru că după ce am parcurs un drum de-a lungul cercului am ajuns la punctul de plecare. A.

Să luăm în considerare unde va fi situat punctul.Deoarece știm deja care este lungimea cercului, îl vom reduce la forma (patru pi plus trei pi cu doi). Adică, trecând din punctul A în direcția pozitivă, trebuie să descrii un întreg cerc de două ori (o cale de lungime 4π) și, în plus, o cale de lungime care se termină în punctul D.

Ce s-a întâmplat? Acesta este 3∙2π + π (de trei ori de două pi plus pi). Aceasta înseamnă că, deplasând din punctul A în direcția pozitivă, trebuie să descrii un cerc întreg de trei ori și, în plus, o cale de lungime π, care se va termina în punctul C.

Pentru a găsi un punct pe cercul numeric care corespunde unui număr negativ, trebuie să mergeți din punctul A de-a lungul cercului în direcția negativă (în sensul acelor de ceasornic) o cale de lungime, iar aceasta corespunde cu 2π +. Această cale se va termina în punctul D.

EXEMPLU 2. Găsiți puncte pe cercul numeric (pi cu șase, pi cu patru, pi cu trei).

Soluţie. Împărțind arcul AB în jumătate, obținem punctul E, care corespunde. Și împărțind arcul AB în trei părți egale prin punctele F și O, obținem că punctul F corespunde, iar punctul T corespunde

(vezi figura 2).

EXEMPLU 3. Găsiți puncte pe cercul numeric (minus treisprezece pi pe patru, nouăsprezece pi pe șase).

Soluţie. Depunând arcul AE (a em) de lungime (pi cu patru) din punctul A de treisprezece ori în direcția negativă, obținem punctul H (cenusa) - mijlocul arcului BC.

Depunând un arc AF de lungime (pi cu șase) din punctul A de nouăsprezece ori în direcția pozitivă, ajungem la punctul N (en), care aparține celui de-al treilea sfert (arc CD) și CN este egal cu a treia parte a arc CD (se de).

(vezi figura exemplu 2).

Cel mai adesea trebuie să cauți pe cercul numeric puncte care corespund numerelor (pi cu șase, pi cu patru, pi cu trei, pi cu doi), precum și pe cele care sunt multipli ale acestora, adică (șapte pi cu șase, cinci pi cu patru, patru pi cu trei, unsprezece pi cu doi). Prin urmare, pentru a naviga rapid, este recomandabil să faceți două aspecte ale cercului numeric.

Pe primul aspect, fiecare dintre sferturile cercului numeric va fi împărțit în două părți egale și lângă fiecare dintre punctele rezultate le vom scrie „numele”:

Pe al doilea aspect, fiecare dintre sferturi este împărțit în trei părți egale și lângă fiecare dintre cele douăsprezece puncte rezultate le scriem „numele”:

Dacă ne mișcăm în sensul acelor de ceasornic, vom obține aceleași „nume” pentru punctele de pe desene, doar cu o valoare în minus. Pentru primul aspect:

În mod similar, dacă vă deplasați de-a lungul celui de-al doilea aspect în sensul acelor de ceasornic din punctul O.

EXEMPLU 4. Găsiți puncte pe cercul numeric care corespund numerelor 1 (unu).

Soluţie. Știind că π≈3,14 (pi este aproximativ egal cu trei virgulă paisprezece sutimi), ≈ 1,05 (pi ori trei este aproximativ egal cu un virgul cinci sutimi), ≈ 0,79 (pi ori patru este aproximativ egal cu zero virgulă șaptezeci și nouă sutimi) . Mijloace,< 1 < (один больше, чем пи на четыре, но меньше, чем пи на три), то есть число 1 находится в первой четверти.

Următoarea afirmație este adevărată: dacă un punct M de pe cercul numeric corespunde unui număr t, atunci acesta corespunde oricărui număr de forma t + 2πk(te plus doi pi ka), unde ka este orice număr întreg și kϵ Z(ka aparține lui Zet).

Folosind această afirmație, putem concluziona că punctul corespunde tuturor punctelor de forma t =+ 2πk (te este egal cu pi ori trei plus două vârfuri), unde kϵZ ( ka aparține zet), iar la punctul (cinci pi pe patru) - puncte de forma t = + 2πk (te este egal cu cinci pi pe patru plus doi pi ka), unde kϵZ ( ka aparține lui zet) și așa mai departe.

EXEMPLU 5. Aflați punctul de pe cercul numeric: a) ; b) .

Soluţie. a) Avem: = =(6 +) ∙ π = 6π + = + 3∙ 2π.(douăzeci de pi ori trei egal de douăzeci de ori trei pi egal șase plus două treimi, înmulțit cu pi egal șase pi plus două pi ori trei egal doi pi ori trei plus trei ori doi pi).

Aceasta înseamnă că numărul corespunde aceluiași punct de pe cercul numeric ca și numărul (acesta este al doilea trimestru) (vezi al doilea aspect din Fig. 4).

b) Avem: = - (8 +) ∙ π = + 2π ∙ (- 4).(minus treizeci și cinci pi ori patru este egal cu minus opt plus trei sferturi ori pi este egal cu minus trei pi ori patru plus două pi ori minus patru ). Adică, numărul corespunde aceluiași punct de pe cercul numeric cu numărul

În această lecție ne vom aminti definiția unei drepte numerice și vom oferi o nouă definiție a unui cerc numeric. De asemenea, vom lua în considerare în detaliu o proprietate importantă a cercului numeric și punctele importante de pe cerc. Să definim problemele directe și inverse pentru cercul numeric și să rezolvăm câteva exemple de astfel de probleme.

Tema: Funcții trigonometrice

Lecția: Cercul numerelor

Pentru orice funcție, argumentul independent este amânat fie de linie numerică, sau pe un cerc. Să caracterizăm atât linia numerică cât și cerc numeric.

Linia dreaptă devine o linie numerică (de coordonate) dacă este marcată originea coordonatelor și sunt selectate direcția și scara (Fig. 1).

Linia numerică stabilește o corespondență unu-la-unu între toate punctele de pe linie și toate numerele reale.

De exemplu, luăm un număr și îl punem pe axa de coordonate, obținem un punct.Luăm un număr și îl punem pe axă, obținem un punct (Fig. 2).

Și invers, dacă luăm orice punct de pe linia de coordonate, atunci există un număr real unic care îi corespunde (Fig. 2).

Oamenii nu au venit imediat la o astfel de corespondență. Pentru a înțelege acest lucru, să ne amintim seturile numerice de bază.

Mai întâi am introdus un set de numere naturale

Apoi un set de numere întregi

Set de numere raționale

S-a presupus că aceste mulțimi ar fi suficiente și că ar exista o corespondență unu-la-unu între toate numerele raționale și punctele de pe o dreaptă. Dar s-a dovedit că există nenumărate puncte pe linia numerică care nu pot fi descrise prin numerele formei

Un exemplu este ipotenuza unui triunghi dreptunghic cu catetele 1 și 1. Este egală (Fig. 3).

Printre mulțimea numerelor raționale, există un număr exact egal cu Nu, nu există. Să demonstrăm acest fapt.

Să demonstrăm prin contradicție. Să presupunem că există o fracție egală cu i.e.

Apoi punem la patrat ambele laturi Evident, latura dreapta a egalitatii este divizibila cu 2, . Aceasta înseamnă și Apoi Dar apoi și A înseamnă Atunci se dovedește că fracția este reductibilă. Acest lucru contrazice condiția, ceea ce înseamnă

Numărul este irațional. Mulțimea numerelor raționale și iraționale formează mulțimea numerelor reale Dacă luăm orice punct de pe o dreaptă, un număr real îi va corespunde. Și dacă luăm orice număr real, va exista un singur punct corespunzător acestuia pe linia de coordonate.

Să clarificăm ce este un cerc numeric și care sunt relațiile dintre mulțimea de puncte de pe cerc și mulțimea numerelor reale.

Origine - punct A. Sensul de numărare - în sens invers acelor de ceasornic - pozitiv, în sensul acelor de ceasornic - negativ. Scara - circumferinta (Fig. 4).

Introducând aceste trei prevederi, avem cerc numeric. Vom indica cum să atribuiți un punct pe un cerc fiecărui număr și invers.

Prin setarea numărului obținem un punct pe cerc

Fiecare număr real corespunde unui punct de pe cerc. Dar invers?

Punctul corespunde numărului. Și dacă luăm numere, toate aceste numere au un singur punct în imaginea lor pe cerc

De exemplu, corespunde punctului B(Fig. 4).

Să luăm toate numerele.Toate corespund punctului. B. Nu există o corespondență unu-la-unu între toate numerele reale și punctele dintr-un cerc.

Dacă există un număr fix, atunci numai un punct de pe cerc îi corespunde

Dacă există un punct pe un cerc, atunci există un set de numere care îi corespunde

Spre deosebire de linie dreaptă, un cerc de coordonate nu are o corespondență unu-la-unu între puncte și numere. Fiecare număr corespunde unui singur punct, dar fiecărui punct îi corespunde un număr infinit de numere și le putem nota.

Să ne uităm la punctele principale ale cercului.

Dat un număr, găsiți punctului din cerc căruia îi corespunde.

Împărțind arcul în jumătate, obținem un punct (Fig. 5).

Problemă inversă: dat un punct în mijlocul unui arc, găsiți toate numerele reale care îi corespund.

Să marchem toate arcele multiple pe cercul numeric (Fig. 6).

Arce care sunt multipli de

Este dat un număr. Trebuie să găsiți punctul corespunzător.

Problemă inversă - dat un punct, trebuie să găsiți numerelor cărora le corespunde.

Am analizat două sarcini standard în două puncte critice.

a) Găsiți un punct pe cercul numeric cu coordonate

Întârziere de la punct A sunt două ture întregi și încă o jumătate și obținem un punct M- acesta este mijlocul celui de-al treilea trimestru (Fig. 8).

Răspuns. Punct M- mijlocul celui de-al treilea trimestru.

b) Găsiți un punct pe cercul numeric cu coordonate

Întârziere de la punct A o întoarcere completă și încă primim un punct N(Fig. 9).

Răspuns: Punct N este in primul trimestru.

Ne-am uitat la linia numerică și la cercul numeric și ne-am amintit caracteristicile lor. O caracteristică specială a dreptei numerice este corespondența unu-la-unu dintre punctele acestei linii și mulțimea numerelor reale. Nu există o astfel de corespondență unu-la-unu pe cerc. Fiecare număr real de pe cerc corespunde unui singur punct, dar fiecărui punct din cerc numeric îi corespunde un număr infinit de numere reale.

În lecția următoare ne vom uita la cercul numeric din planul de coordonate.

Lista de referințe la subiectul „Cercul numărului”, „Punct pe un cerc”

1. Algebră și început de analiză, nota 10 (în două părți). Manual pentru instituțiile de învățământ general (nivel de profil), ed. A. G. Mordkovici. -M.: Mnemosyne, 2009.

2. Algebră și început de analiză, nota 10 (în două părți). Cartea de probleme pentru instituțiile de învățământ (nivel de profil), ed. A. G. Mordkovici. -M.: Mnemosyne, 2007.

3. Vilenkin N.Ya., Ivashev-Musatov O.S., Shvartsburd S.I. Algebră și analiză matematică pentru clasa a 10-a (manual pentru elevii școlilor și claselor cu studiu aprofundat al matematicii). - M.: Prosveshchenie, 1996.

4. Galitsky M.L., Moshkovich M.M., Shvartburd S.I. Studiu aprofundat al algebrei și analizei matematice.-M.: Educație, 1997.

5. Culegere de probleme de matematică pentru solicitanții la instituțiile de învățământ superior (editat de M.I. Skanavi).- M.: Liceu, 1992.

6. Merzlyak A.G., Polonsky V.B., Yakir M.S. Simulator algebric.-K.: A.S.K., 1997.

7. Sahakyan S.M., Goldman A.M., Denisov D.V. Probleme de algebră și principii de analiză (manual pentru elevii din clasele 10-11 din instituțiile de învățământ general) - M.: Prosveshchenie, 2003.

8. Karp A.P. Culegere de probleme de algebră și principii de analiză: manual. indemnizatie pentru 10-11 clase. cu profunzime studiat Matematică.-M.: Educaţie, 2006.

Teme pentru acasă

Algebră și început de analiză, nota 10 (în două părți). Cartea de probleme pentru instituțiile de învățământ (nivel de profil), ed. A. G. Mordkovici. -M.: Mnemosyne, 2007.

№№ 11.6 - 11.12, 11.15 - 11.17.

Resurse web suplimentare

3. Portal educațional pentru pregătirea examenelor ().

Materiale suplimentare
Dragi utilizatori, nu uitați să lăsați comentariile, recenziile, urările! Toate materialele au fost verificate de un program antivirus.

Manuale si simulatoare in magazinul online Integral pentru nota 10 din 1C
Probleme algebrice cu parametri, clasele 9–11
Mediul software „1C: Mathematical Constructor 6.1”

Cercul numeric și viața

În viața reală, mișcarea circulară este obișnuită. De exemplu, competiții ale bicicliștilor care parcurg un anumit tur cu un timp limită sau competiții ale mașinilor de curse care trebuie să parcurgă cele mai multe tururi în timpul alocat.

Un alergător aleargă într-un cerc lung de 400 de metri. Sportivul începe din punctul A (Fig. 1) și se deplasează în sens invers acelor de ceasornic. Unde va fi la 200 m, 800 m, 1500 m? Unde ar trebui trasată linia de sosire dacă un alergător trebuie să alerge 4195 m?

Soluţie:
După 200 m alergătorul va fi în punctul C. Deoarece va fi alergat exact jumătate din distanță.

După ce a alergat 800 m, alergătorul va face exact două cercuri și va ajunge în punctul A.

1500m reprezintă 3 ture de 400m (1200m) și încă 300m, adică $\frac(3)(4)$ de la pista de alergare, finalul acestei distanțe este în punctul D.

Unde va fi alergătorul nostru după ce a alergat 4195 m? 10 ture înseamnă 4000 m, mai ai 195 m de alergat, adică cu 5 m mai puțin decât jumătate din distanță. Aceasta înseamnă că finisajul va fi în punctul K, situat lângă punctul C.

Definiția cercului numeric

Vedere generală a cercului numeric

Diametrele AC și BD împart cercul în patru sferturi:
primul sfert– acesta este arcul AB.
Al doilea sfert– arc BC.
al treilea trimestru– arc CD.
al patrulea sfert– arc DA.

3) punct de start cerc numeric – punctul A.
Numărarea din punctul A în sens invers acelor de ceasornic se numește direcție pozitivă. Numărarea din punctul A în sensul acelor de ceasornic se numește direcție negativă.

Lungimea cercului numeric

Localizarea punctelor principale ale cercului

Fiecare dintre cele patru sferturi ale cercului numeric este împărțit în trei părți egale. Alaturi de fiecare dintre cele douasprezece puncte obtinute se scrie numarul caruia ii corespunde.

Dacă punctul $M$ al cercului numeric corespunde unui număr $t$, atunci îi corespunde și unui număr de forma $t+2π *k$, unde $k$ este un număr întreg. $M(t) = M(t+2π*k)$.

Lungimea arcului $AB =\frac(π)(2)$. Împărțind-o în două părți egale cu punctul M, obținem două arce, fiecare de lungime $\frac(π)(4)$. Aceasta înseamnă $AM =МВ=\frac(π)(4)$.

Arcul AB este împărțit în trei părți egale prin punctele K și P. Lungimea fiecărei părți rezultate este egală cu $\frac(1)(3)* \frac(π)(2)$, adică $\frac(π) (6) $. Aceasta înseamnă $AK = KR = PB =\frac(π)(6)$.

Arcul AR este format din două arce AK și KR de lungime - $\frac(π)(6)$. Aceasta înseamnă $AP = 2 *\frac(π)(6) =\frac(π)(3)$.

Rămâne de calculat lungimea arcului CM. Acest arc se obține din arcul AM cu excepția arcului AK. Astfel, $KM = AM – AK =\frac(π)(4) - \frac(π)(6) = \frac(π)(12)$.

Sarcină:

Găsiți un punct pe cercul numeric care corespunde unui număr dat:
$2π$, $\frac(7π)(2)$, $\frac(π)(4)$, $-\frac(3π)(2)$.

Numărul $2π$ corespunde punctului A, deoarece după ce a trecut o cale de lungime $2π$ în jurul cercului, adică. exact un cerc, vom ajunge din nou la punctul A.

Numărul $\frac(7π)(2)$ corespunde punctului D, deoarece $\frac(7π)(2)=2π+\frac(3π)(2)$, adică. deplasându-vă în direcția pozitivă, trebuie să treceți printr-un cerc întreg și o cale suplimentară de lungime $\frac(3π)(2)$, care se va termina în punctul D.

Numărul $\frac(π)(4)$ corespunde punctului M, deoarece deplasându-vă în direcția pozitivă, trebuie să parcurgeți o cale de jumătate de arc AB de lungime $\frac(π)(2)$, care se va termina în punctul M.

Numărul $-\frac(3π)(2)$ corespunde punctului B, deoarece deplasându-vă într-o direcție negativă din punctul A, trebuie să parcurgeți o cale de lungime $\frac(3π)(2)$ care se termină în punctul B.

Găsiți puncte pe cercul numeric:
a) $21\frac(π)(4)$;
b) $-37\frac(π)(6)$.

a) $\frac(21π)(4) = (4+\frac(5)(4))*π = 4π +\frac(5π)(4) = 2*2π +\frac(5π)(4) $, ceea ce înseamnă că numărul $\frac(21π)(4)$ corespunde aceluiași număr cu numărul $\frac(5)(4π)$ – mijlocul celui de-al treilea trimestru.

b) $-\frac(37π)(6)=-(6+\frac(1)(6))*π =-(6π +\frac(π)(6)) = -3*2π - \frac (π )(6)$. Aceasta înseamnă că numărul $-\frac(37π)(6)$ corespunde aceluiași număr cu numărul $-\frac(1)(6π)$. La fel ca $\frac(11π)(6)$.

Găsiți toate numerele t care corespund punctelor cercului numeric care aparțin unui arc dat:
a) VA;
b) MK.

a) Arcul BA este un arc cu început în punctul B și sfârșit în punctul A, care se deplasează de-a lungul unui cerc în sens invers acelor de ceasornic. Punctul B este egal cu $\frac(π)(2)$, iar punctul A este egal cu $2π$. Aceasta înseamnă că pentru punctele t avem: $\frac(π)(2) ≤ t ≤ 2π$. Dar, conform formulei de pe diapozitivul 8, numerele $\frac(π)(2)$ și $2π$ corespund numerelor de forma $\frac(π)(2)+2π*k$ și $2π+2π *k$, respectiv.

$\frac(π)(2) +2π*k ≤ t ≤ 2π +2π*k$, unde $k$ este un număr întreg.

b) Arcul MK este un arc cu început în punctul M și sfârșit în punctul K. Punctul M este egal cu $-\frac(3π)(4)$ și punctul K este egal cu $\frac(π) (4)$.
Deci pentru punctele t avem:
$\frac(-3π)(4) ≤ t ≤\frac(π)(4)$.
Conform formulei din slide 8, numerele $-\frac(3π)(4)$ și $\frac(π)(4)$ corespund numerelor de forma: $-\frac(3π)(4)+ 2π*k$ și, respectiv, $\ frac(π)(4)+2π*k$.
Atunci numărul nostru t ia următoarele valori:
$-\frac(3π)(4)+2π*k ≤ t ≤ \frac(π)(4) +2π*k$, unde $k$ este un număr întreg.

Probleme de rezolvat independent

1) Pe cercul unitar, arcul BC este împărțit de punctul T în două părți egale, iar de punctele K și P în trei părți egale. Care este lungimea arcului: VT, TS, VK, KR, RS, VR, CT?

2) Găsiți un punct pe cercul numeric care corespunde unui număr dat:
$π$, $\frac(11π)(2)$, $\frac(21π)(4)$, $-\frac(7π)(2)$, $\frac(17π)(6)$.

3) Aflați toate numerele t, care pe cercul numeric corespund punctelor aparținând unui arc dat:
a) AB;
b) AC;
c) PM, unde P este punctul de mijloc al arcului AB, iar punctul M este punctul de mijloc al lui DA.