Un paralelipiped drept cu bază pătrată. Paralelepiped și cub. Ghid vizual (2019). Ce tipuri de paralelipiped există?

Obiectivele lecției:

1. Educațional:

Introduceți conceptul de paralelipiped și tipurile acestuia;
- formulați (folosind analogia cu un paralelogram și un dreptunghi) și dovediți proprietățile unui paralelipiped și unui cuboid;
- repeta întrebări legate de paralelism și perpendicularitate în spațiu.

2. Dezvoltare:

Continuarea dezvoltării proceselor cognitive la elevi precum percepția, înțelegerea, gândirea, atenția, memoria;
- promovează dezvoltarea elementelor de activitate creativă la elevi ca calități ale gândirii (intuiție, gândire spațială);
- să dezvolte la elevi capacitatea de a trage concluzii, inclusiv prin analogie, care ajută la înțelegerea legăturilor intra-subiecte în geometrie.

3. Educativ:

Contribuie la dezvoltarea organizării și a obiceiurilor de muncă sistematică;
- contribuie la formarea deprinderilor estetice la realizarea notelor si realizarea desenelor.

Tip de lecție: lecție-învățare material nou (2 ore).

Structura lecției:

1. Moment organizatoric.
2. Actualizarea cunoștințelor.
3. Studierea materialelor noi.
4. Rezumarea și stabilirea temelor.

Echipamente: postere (diapozitive) cu dovezi, machete ale diverselor corpuri geometrice, inclusiv toate tipurile de paralelipipedi, proiector grafic.

În timpul orelor.

1. Moment organizatoric.

2. Actualizarea cunoștințelor.

Comunicarea temei lecției, formularea scopurilor și obiectivelor împreună cu elevii, arătând semnificația practică a studierii temei, repetarea problemelor studiate anterior legate de această temă.

3. Studierea materialelor noi.

3.1. Paralelepiped și tipurile sale.

Sunt demonstrate modele de paralelipiped, identificându-se caracteristicile acestora, care ajută la formularea definiției unui paralelipiped folosind conceptul de prismă.

Definiție:

paralelipiped numită prismă a cărei bază este un paralelogram.

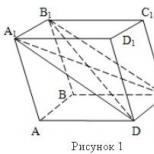
Se realizează un desen al unui paralelipiped (Figura 1), sunt enumerate elementele unui paralelipiped ca caz special al unei prisme. Diapozitivul 1 este afișat.

Notarea schematică a definiției:

Se formulează concluziile din definiție:

1) Dacă ABCDA 1 B 1 C 1 D 1 este o prismă și ABCD este un paralelogram, atunci ABCDA 1 B 1 C 1 D 1 – paralelipiped.

2) Dacă ABCDA 1 B 1 C 1 D 1 – paralelipiped, atunci ABCDA 1 B 1 C 1 D 1 este o prismă și ABCD este un paralelogram.

3) Dacă ABCDA 1 B 1 C 1 D 1 nu este o prismă sau ABCD nu este un paralelogram, atunci
ABCDA 1 B 1 C 1 D 1 – nu paralelipiped.

4) . Dacă ABCDA 1 B 1 C 1 D 1 – nu paralelipiped, atunci ABCDA 1 B 1 C 1 D 1 nu este o prismă sau ABCD nu este un paralelogram.

În continuare, sunt luate în considerare cazuri speciale ale unui paralelipiped cu construirea unei scheme de clasificare (vezi Fig. 3), sunt demonstrate modele, sunt evidențiate proprietățile caracteristice ale paralelipipedelor drepte și dreptunghiulare și sunt formulate definițiile acestora.

Definiție:

Un paralelipiped se numește drept dacă marginile sale laterale sunt perpendiculare pe bază.

Definiție:

Paralepipedul se numește dreptunghiular, dacă marginile sale laterale sunt perpendiculare pe bază, iar baza este un dreptunghi (vezi Figura 2).

După înregistrarea definițiilor într-o formă schematică, se formulează concluzii din acestea.

3.2. Proprietățile paralelipipedelor.

Căutați figuri planimetrice ale căror analogi spațiali sunt paralelipiped și cuboid (paralelogram și dreptunghi). În acest caz, avem de-a face cu asemănarea vizuală a figurilor. Folosind regula de inferență prin analogie, tabelele sunt completate.

Regula de inferență prin analogie:

1. Selectați dintre cifrele studiate anterior o cifră similară cu aceasta.
2. Formulați proprietatea figurii selectate.
3. Formulați o proprietate similară a figurii originale.
4. Demonstrați sau infirmați afirmația formulată.

După formularea proprietăților, demonstrarea fiecăreia dintre ele se efectuează conform următoarei scheme:

• discutarea planului de probă;
• demonstrarea unui diapozitiv cu dovezi (diapozitivele 2 – 6);
• Elevii completând dovezi în caiete.

3.3 Cubul și proprietățile sale.

Definiție: Un cub este un paralelipiped dreptunghiular în care toate cele trei dimensiuni sunt egale.

Prin analogie cu un paralelipiped, elevii fac independent o notație schematică a definiției, derivă consecințe din aceasta și formulează proprietățile cubului.

4. Rezumarea și stabilirea temelor.

Teme pentru acasă:

1. Folosind notele de lecție din manualul de geometrie pentru clasele 10-11, L.S. Atanasyan și alții, studiază Capitolul 1, §4, paragraful 13, Capitolul 2, §3, paragraful 24.
2. Demonstrați sau infirmați proprietatea unui paralelipiped, punctul 2 din tabel.
3. Răspunde la întrebări de securitate.

Întrebări de control.

1. Se știe că doar două fețe laterale ale paralelipipedului sunt perpendiculare pe bază. Ce tip de paralelipiped?

2. Câte fețe laterale de formă dreptunghiulară poate avea un paralelipiped?

3. Este posibil să existe un paralelipiped cu o singură față laterală:

1) perpendicular pe bază;
2) are forma unui dreptunghi.

4. Într-un paralelipiped drept, toate diagonalele sunt egale. Este dreptunghiular?

5. Este adevărat că într-un paralelipiped drept secțiunile diagonale sunt perpendiculare pe planurile bazei?

6. Prezentați teorema inversă cu teorema despre pătratul diagonalei unui paralelipiped dreptunghic.

7. Ce caracteristici suplimentare disting un cub de un paralelipiped dreptunghiular?

8. Va fi un paralelipiped un cub în care toate muchiile de la unul dintre vârfuri sunt egale?

9. Prezentați teorema pe pătratul diagonalei unui cuboid pentru cazul unui cub.

În această lecție, toată lumea va putea studia subiectul „Paralepiped dreptunghiular”. La începutul lecției, vom repeta ce sunt paralelipipedele drepte și arbitrare, amintiți-vă proprietățile fețelor și diagonalelor lor opuse ale paralelipipedului. Apoi ne vom uita la ce este un cuboid și vom discuta proprietățile sale de bază.

Tema: Perpendicularitatea dreptelor și a planurilor

Lecția: Cuboid

O suprafață compusă din două paralelograme egale ABCD și A 1 B 1 C 1 D 1 și patru paralelograme ABV 1 A 1, BCC 1 B 1, CDD 1 C 1, DAA 1 D 1 se numește paralelipiped(Fig. 1).

Orez. 1 Paralelepiped

Adică: avem două paralelograme egale ABCD și A 1 B 1 C 1 D 1 (baze), acestea se află în plane paralele astfel încât marginile laterale AA 1, BB 1, DD 1, CC 1 să fie paralele. Astfel, o suprafață compusă din paralelograme se numește paralelipiped.

Astfel, suprafața unui paralelipiped este suma tuturor paralelogramelor care alcătuiesc paralelipipedul.

1. Fețele opuse ale unui paralelipiped sunt paralele și egale.

(formele sunt egale, adică pot fi combinate prin suprapunere)

De exemplu:

ABCD = A 1 B 1 C 1 D 1 (paralelograme egale prin definiție),

AA 1 B 1 B = DD 1 C 1 C (deoarece AA 1 B 1 B și DD 1 C 1 C sunt fețe opuse ale paralelipipedului),

AA 1 D 1 D = BB 1 C 1 C (deoarece AA 1 D 1 D și BB 1 C 1 C sunt fețe opuse ale paralelipipedului).

2. Diagonalele unui paralelipiped se intersectează într-un punct și sunt tăiate în două de acest punct.

Diagonalele paralelipipedului AC 1, B 1 D, A 1 C, D 1 B se intersectează într-un punct O, iar fiecare diagonală este împărțită la jumătate de acest punct (Fig. 2).

Orez. 2 Diagonalele unui paralelipiped se intersectează și sunt împărțite la jumătate la punctul de intersecție.

3. Există trei cvadruple de margini egale și paralele ale unui paralelipiped: 1 - AB, A 1 B 1, D 1 C 1, DC, 2 - AD, A 1 D 1, B 1 C 1, BC, 3 - AA 1, BB 1, CC 1, DD 1.

Definiție. Un paralelipiped se numește drept dacă marginile sale laterale sunt perpendiculare pe baze.

Lăsați marginea laterală AA 1 să fie perpendiculară pe bază (Fig. 3). Aceasta înseamnă că dreapta AA 1 este perpendiculară pe liniile drepte AD și AB, care se află în planul bazei. Aceasta înseamnă că fețele laterale conțin dreptunghiuri. Și bazele conțin paralelograme arbitrare. Să notăm ∠BAD = φ, unghiul φ poate fi oricare.

Orez. 3 Paralepipedul drept

Deci, un paralelipiped drept este un paralelipiped în care marginile laterale sunt perpendiculare pe bazele paralelipipedului.

Definiție. Paralepipedul se numește dreptunghiular, dacă marginile sale laterale sunt perpendiculare pe bază. Bazele sunt dreptunghiuri.

Paralelepipedul ABCDA 1 B 1 C 1 D 1 este dreptunghiular (Fig. 4), dacă:

1. AA 1 ⊥ ABCD (margine laterală perpendiculară pe planul bazei, adică paralelipiped drept).

2. ∠BAD = 90°, adică baza este un dreptunghi.

Orez. 4 Paralepiped dreptunghiular

Un paralelipiped dreptunghiular are toate proprietățile unui paralelipiped arbitrar. Dar există proprietăți suplimentare care sunt derivate din definiția unui cuboid.

Asa de, cuboid este un paralelipiped ale cărui margini laterale sunt perpendiculare pe bază. Baza unui cuboid este un dreptunghi.

1. Într-un paralelipiped dreptunghiular, toate cele șase fețe sunt dreptunghiuri.

ABCD și A 1 B 1 C 1 D 1 sunt dreptunghiuri prin definiție.

2. Coastele laterale sunt perpendiculare pe bază. Aceasta înseamnă că toate fețele laterale ale unui paralelipiped dreptunghiular sunt dreptunghiuri.

3. Toate unghiurile diedrice ale unui paralelipiped dreptunghiular sunt drepte.

Să considerăm, de exemplu, unghiul diedric al unui paralelipiped dreptunghic cu muchia AB, adică unghiul diedric dintre planele ABC 1 și ABC.

AB este o muchie, punctul A 1 se află într-un plan - în planul ABB 1, iar punctul D în celălalt - în planul A 1 B 1 C 1 D 1. Atunci unghiul diedric luat în considerare mai poate fi notat astfel: ∠A 1 ABD.

Să luăm punctul A pe muchia AB. AA 1 este perpendicular pe muchia AB în planul АВВ-1, AD este perpendicular pe muchia AB în planul ABC. Aceasta înseamnă că ∠A 1 AD este unghiul liniar al unui unghi diedric dat. ∠A 1 AD = 90°, ceea ce înseamnă că unghiul diedrului la muchia AB este de 90°.

∠(ABB 1, ABC) = ∠(AB) = ∠A 1 ABD= ∠A 1 AD = 90°.

În mod similar, se dovedește că orice unghiuri diedrice ale unui paralelipiped dreptunghic sunt drepte.

Pătratul diagonalei unui paralelipiped dreptunghic este egal cu suma pătratelor celor trei dimensiuni ale sale.

Notă. Lungimile celor trei muchii care emană dintr-un vârf al unui cuboid sunt măsurătorile cuboidului. Ele sunt uneori numite lungime, lățime, înălțime.

Dat: ABCDA 1 B 1 C 1 D 1 - paralelipiped dreptunghiular (Fig. 5).

Demonstrați: .

Orez. 5 Paralepiped dreptunghiular

Dovada:

Linia dreaptă CC 1 este perpendiculară pe planul ABC și, prin urmare, pe dreapta AC. Aceasta înseamnă că triunghiul CC 1 A este dreptunghic. Conform teoremei lui Pitagora:

Luați în considerare triunghiul dreptunghic ABC. Conform teoremei lui Pitagora:

Dar BC și AD sunt laturi opuse ale dreptunghiului. Deci BC = AD. Apoi:

Deoarece , A , Acea. Deoarece CC 1 = AA 1, acesta este ceea ce trebuia demonstrat.

Diagonalele unui paralelipiped dreptunghiular sunt egale.

Să notăm dimensiunile paralelipipedului ABC ca a, b, c (vezi Fig. 6), apoi AC 1 = CA 1 = B 1 D = DB 1 =

Deoarece toate fețele unui paralelipiped sunt paralelograme, atunci linia AD este paralelă cu dreapta BC, iar linia este paralelă cu dreapta . Rezultă că planurile fețelor luate în considerare sunt paralele.

Din faptul că fețele unui paralelipiped sunt paralelograme, rezultă că AB, , CD sunt paralele și egale. De aici concluzionăm că fața este combinată prin translație paralelă de-a lungul muchiei AB cu fața. Prin urmare, aceste margini sunt egale.

2 ) Să luăm două diagonale ale paralelipipedului (Fig. 5), de exemplu, și , și să desenăm drepte suplimentare și . AB și respectiv sunt egale și paralele cu muchia DC, prin urmare sunt egale și paralele între ele; Ca urmare, figura este un paralelogram în care liniile drepte și sunt diagonalele, iar într-un paralelogram diagonalele sunt împărțite la jumătate în punctul de intersecție. În mod similar, putem demonstra că celelalte două diagonale se intersectează într-un punct și sunt tăiate în două de acel punct. Punctul de intersecție al fiecărei perechi de diagonale se află în mijlocul diagonalei. Astfel, toate cele patru diagonale ale paralelipipedului se intersectează într-un punct O și sunt bisectate de acest punct. Astfel, punctul de intersecție al diagonalelor unui paralelipiped este centrul său de simetrie.

Teorema:

Pătratul diagonalei unui paralelipiped dreptunghic este egal cu suma pătratelor celor trei dimensiuni ale sale.

Dovada:

Acest lucru reiese din teorema spațială a lui Pitagora. Dacă este diagonala unui paralelipiped dreptunghic , apoi sunt proiecțiile sale pe trei linii perpendiculare perechi (Fig. 6). Prin urmare, .

Teorema. În orice paralelipiped, fețele opuse sunt egale și paralele.

Astfel, fețele (Fig.) BB 1 C 1 C și AA 1 D 1 D sunt paralele, deoarece două drepte care se intersectează BB 1 și B 1 C 1 ale unei fețe sunt paralele cu două drepte care se intersectează AA 1 și A 1 D 1 ale celălalt. Aceste fețe sunt egale, deoarece B 1 C 1 =A 1 D 1, B 1 B=A 1 A (ca laturi opuse ale paralelogramelor) și ∠BB 1 C 1 = ∠AA 1 D 1.

Teorema. În orice paralelipiped, toate cele patru diagonale se intersectează într-un punct și sunt încrucișate în el.

Să luăm (Fig.) vreo două diagonale în paralelipiped, de exemplu, AC 1 și DB 1, și să desenăm linii drepte AB 1 și DC 1.

Deoarece muchiile AD și B 1 C 1 sunt egale și, respectiv, paralele cu muchia BC, atunci ele sunt egale și paralele între ele.

Ca urmare, figura ADC 1 B 1 este un paralelogram în care C 1 A și DB 1 sunt diagonale, iar într-un paralelogram diagonalele se intersectează în jumătate.

Această demonstrație poate fi repetată la fiecare două diagonale.

Prin urmare, diagonala AC 1 intersectează BD 1 în jumătate, diagonala BD 1 intersectează A 1 C în jumătate.

Astfel, toate diagonalele se intersectează în jumătate și, prin urmare, într-un punct.

Teorema. Într-un paralelipiped dreptunghiular, pătratul oricărei diagonale este egal cu suma pătratelor celor trei dimensiuni ale sale.

Fie (Fig.) AC 1 o diagonală a unui paralelipiped dreptunghic.

Desenând AC, obținem două triunghiuri: AC 1 C și ACB. Ambele sunt dreptunghiulare:

primul deoarece paralelipipedul este drept și, prin urmare, muchia CC 1 este perpendiculară pe bază,

al doilea deoarece paralelipipedul este dreptunghiular, ceea ce înseamnă că la baza lui există un dreptunghi.

Din aceste triunghiuri găsim:

AC 2 1 = AC 2 + CC 2 1 și AC 2 = AB 2 + BC 2

Prin urmare, AC 2 1 = AB 2 + BC 2 + CC 2 1 = AB 2 + AD 2 + AA 2 1

Consecinţă. Într-un paralelipiped dreptunghic toate diagonalele sunt egale.

Sau (echivalent) un poliedru, care are șase fețe și fiecare dintre ele - paralelogram.

Tipuri de paralelipiped

Există mai multe tipuri de paralelipipede:

• Un cuboid este un paralelipiped ale cărui fețe sunt toate dreptunghiuri.
• Un paralelipiped drept este un paralelipiped cu 4 fețe laterale care sunt dreptunghiuri.
• Un paralelipiped înclinat este un paralelipiped ale cărui fețe laterale nu sunt perpendiculare pe baze.

Elemente esentiale

Două fețe ale unui paralelipiped care nu au o muchie comună sunt numite opuse, iar cele care au o muchie comună sunt numite adiacente. Două vârfuri ale unui paralelipiped care nu aparțin aceleiași fețe sunt numite opuse. Segmentul care leagă vârfuri opuse se numește diagonala paralelipipedului. Lungimile a trei muchii ale unui paralelipiped dreptunghiular care au un vârf comun se numesc dimensiunile sale.

Proprietăți

• Paralepipedul este simetric în jurul mijlocului diagonalei sale.
• Orice segment cu capete aparținând suprafeței paralelipipedului și care trece prin mijlocul diagonalei acestuia este împărțit în jumătate de acesta; în special, toate diagonalele unui paralelipiped se intersectează într-un punct și sunt tăiate în două de acesta.
• Fețele opuse ale unui paralelipiped sunt paralele și egale.
• Pătratul lungimii diagonale a unui paralelipiped dreptunghic este egal cu suma pătratelor celor trei dimensiuni ale sale.

Formule de bază

Paralepipedul drept

Suprafata laterala S b =P o *h, unde P o este perimetrul bazei, h este înălțimea

Suprafata totala S p =S b +2S o, unde S o este aria bazei

Volum V=S o *h

Paralepiped dreptunghiular

Suprafata laterala S b =2c(a+b), unde a, b sunt laturile bazei, c este marginea laterală a paralelipipedului dreptunghiular

Suprafata totala S p =2(ab+bc+ac)

Volum V=abc, unde a, b, c sunt dimensiunile unui paralelipiped dreptunghic.

cub

Suprafață: $S=6a^2$
Volum: $V=a^3$, Unde $A$- muchia unui cub.

Orice paralelipiped

Volumul și rapoartele dintr-un paralelipiped înclinat sunt adesea determinate folosind algebră vectorială. Volumul unui paralelipiped este egal cu valoarea absolută a produsului mixt a trei vectori determinată de cele trei laturi ale paralelipipedului care emană dintr-un vârf. Relația dintre lungimile laturilor paralelipipedului și unghiurile dintre ele dă afirmația că determinantul Gram al celor trei vectori indicați este egal cu pătratul produsului lor mixt: 215.

În analiza matematică

În analiza matematică sub un cuboid n-dimensional $B$ intelege multe puncte $x\; =\; (x\_1,\backslash ldots,x\_n)$ drăguț $B\; =\; \backslash (x|a\_1\backslash leqslant\; x\_1\backslash leqslant\; b\_1,\backslash ldots,a\_n\backslash leqslant\; x\_n\backslash leqslant\; b\_n\backslash )$

Scrieți o recenzie despre articolul „Paralelepiped”

Note

Legături

Un fragment care caracterizează Paralelepipedul