Semne de convergență a integralelor improprie. Integrale improprii Definiție și proprietăți de bază

Teorema 12.11 (test pentru compararea integralelor improprie). Fie funcțiile f(x) și g(x) să fie continue pe intervalul [a, ">) și să satisfacă condiția 0 fix) ?(x) pe acesta. Apoi de la convergența integralei

urmează convergenţa integralei

și invers, divergența integralei (12.64) implică divergența integralei (12.63).

Dovada. Să introducem notația:

Funcţie P(K) nu este în scădere; de fapt, dacă iar eu 2 , atunci

J repara) dx>0 și apoi

Luați succesiunea valorilor (/? „) -> „>; apoi succesiunea corespunzătoare de valori ale funcției (F(Rn)) este monotonă și nedescrescătoare. Fie ca integrala (12.63) să convergă, apoi șirul (67 ( R it)) este limitat; dar apoi și succesiunea este limitată (F(/?n)) și, prin urmare, în virtutea teoremei 7.13, converge. Prin urmare, există o limită F(R) la R-+ ">, adică integrala (12.64) converge.

Demonstrăm acum partea a doua a teoremei; fie integrala (12.64) diverge. Dacă presupunem că integrala (12.63) converge, atunci prin ceea ce s-a dovedit mai sus trebuie să convergă și integrala (12.64), ceea ce contrazice condiția. Teorema a fost demonstrată. ?

Cometariu. Un criteriu de comparație similar este valabil și pentru integralele improprii de al doilea fel. Dacă funcţiile f(x) şi g (X) continuă pe jumătate de interval [a> b)și pentru toate punctele din vreo vecinătate a punctului singular bîmplinit

conditii 0 (x), atunci din convergența integralei Jg(x)dx rezultă că

integrala J/(x)dx, iar din divergența integralei J/(x)dx - divergența

puntea integralei Jg(x)dx.

Să luăm în considerare exemple pentru studierea convergenței integralelor improprie.

Exemplul 27. T . ^-.

X 3 (1 + e L)

Soluţie. Să comparăm integralul din această integrală cu funcția

Dg. Este evident că -g--

X r* (1+0 x J

gradul J-jdx converge; prin urmare, în virtutea criteriului de comparație converge și 1 X

ny integrală.

Exemplul 28. I-.

Soluţie. Comparând integrantul acestei integrale cu funcția 1/x,

vedem că (1 + In x)/x > 1/x pe intervalul 1

diverge, prin urmare, integrala dată diverge și după criteriul comparației.

În concluzie, prezentăm fără dovezi criteriul Cauchy pentru convergența unei integrale improprie de primul fel.

12.10.4. Convergența absolută și condiționată a integralelor improprie

Definiția 5. Se numește integrală improprie J/(x)dx absolut

convergente, dacă integrala J|/(x)|dx converge.

Definiţia 6. Se numeşte integrala improprie J /(x) dx condițional asemănătoare

mocnit, dacă converge și integrala J|/(x)|dx diverge.

Rețineți că convergența absolută a integralei implică convergența acesteia în virtutea estimării 3 a integralei definite și a criteriului Cauchy.

Teorema 12.13 (testul Dirichlet-Abel*). Fie funcția f(x) continuă și are o antiderivată mărginită F(x) pe intervalul [a, ">), în timp ce funcția g(x) are o derivată continuă pe acest interval, nu crește și tinde spre zero ca x -> ©o. Apoi integrala improprie

converge.

Dovada. Aplicăm integrarea pe părți la integrala J /(x)g(x)dx

pe un segment arbitrar R R" Cu [ A, °°). Avem:

Teorema 12.12. Pentru convergența integralei improprie (12.64) este necesar și suficient ca pentru orice e > 0 să se găsească un astfel de număr A> 0, care pentru orice R"și /?", mai mare decât A, este valabilă următoarea inegalitate:

Conform teoremei F(x) limitat, adică |F(x)| K. Funcția g(x) nu crește și tinde spre zero ca x -» «>, deci. g(x)> 0 și g"(x)

Abel Niels Henrik (1802-1829) matematician norvegian.

Deoarece, prin ipoteza teoremei, g(x) -» 0 ca x -> ©°, pt. număr arbitrar e > 0 puteți găsi numărul A> astfel încât la R"> L inegalitatea va fi îndeplinită g(R") Înlocuind aceasta în estimarea (12.68), obținem:

care corespunde criteriului Cauchy pentru convergenţa integralei (12.66). Teorema a fost demonstrată. ?

Luați în considerare exemple de utilizare a testului Dirichlet-Abel pentru convergența integralelor improprie.

Exemplul 29. f^^dx, a > 0.

Soluţie. Punem / (x) \u003d sin x, g(x)= l/x"; este ușor de verificat dacă toate condițiile teoremei sunt îndeplinite, adică această integrală converge. Pentru a > 1, această integrală

ral converge absolut. Într-adevăr, |păcat x/xP 1/d L, integrală J(l/x e)dx

converge, adică prin comparație (Teorema 12.11), această integrală converge și ea absolut.

Exemplul 30. Jsin x 2 dx - integrala Fresnel, o

Soluţie. Reprezentăm această integrală ca o sumă:

Deoarece sin x 2 este o funcție continuă pe segmentul (0, 1J), prima integrală din (12.69) există. Pentru a determina convergența integralei improprie pe partea dreaptă a lui (12.69), punem / (x) \ u003d x sin x 2, g(x) = 1/x. Atunci pentru funcția f(x) antiderivată F(x) = -cosx 2 /! este mărginită pe intervalul |1, ">), în timp ce #(x) este pozitiv, tinde spre zero ca x -» °° și are o derivată continuă pe (1, ©o). Prin urmare, conform criteriului Dirichlet - Abel, integrala a doua din (12.69) converge, i.e. converge și integrala Fresnel.

Integrale improprii de primul fel. De fapt, aceasta este aceeași integrală definită, dar în cazurile în care integralele au o limită de integrare superioară sau inferioară infinită, sau ambele limite de integrare sunt infinite.

Integrale improprii de al doilea fel. De fapt, aceasta este aceeași integrală definită, dar în cazurile în care integrala este luată din funcții nemărginite, integrandul nu are integrare la un număr finit de puncte ale segmentului finit, transformându-se la infinit.

Pentru comparație. La introducerea conceptului de integrală definită, s-a presupus că funcția f(X) este continuă pe intervalul [ A, b], iar intervalul de integrare este finit, adică este limitat de numere, și nu de infinit. Unele sarcini duc la necesitatea renunțării la aceste restricții. Așa apar integralele improprii.

Sensul geometric al integralei improprie se dovedește a fi destul de simplu. Când graficul funcţiei y = f(X) este deasupra axei Bou, integrala definită exprimă aria trapez curbiliniu, curbă mărginită y = f(X) , abscisă și ordonate X = A , X = b. La rândul său, integrala improprie exprimă aria unui trapez curbiliniu nemărginit (infinit) închis între linii y = f(X) (poza de mai jos cu roșu) X = A iar axa absciselor.

Integrale improprii sunt definite în mod similar pentru alte intervale infinite:

Aria unui trapez curbiliniu infinit poate fi un număr finit, caz în care integrala improprie se numește convergentă. Aria poate fi și infinită, caz în care integrala improprie se numește divergentă.

Folosind limita unei integrale în locul integralei improprie în sine. Pentru a calcula integrala improprie, trebuie să utilizați limita integralei definite. Dacă această limită există și este finită (nu este egală cu infinitul), atunci integrala improprie se numește convergentă, în caz contrar este divergentă. La ce tinde variabila sub semnul limită depinde dacă avem de-a face cu o integrală improprie de primul fel sau de al doilea fel. Să aflăm acum despre asta.

Integrale improprii de primul fel - cu limite infinite și convergența lor

Integrale improprii cu o limită superioară infinită

Deci, înregistrarea integralei improprie diferă de integrala definită obișnuită prin faptul că limita superioară a integrării este infinită.

Definiție. O integrală improprie cu o limită superioară infinită de integrare din functie continua f(X) între A inainte de ∞ se numeste limita integralei acestei functii cu limita superioara a integrarii b și limita inferioară a integrării A cu condiţia ca limita superioară a integrării să crească la nesfârşit, adică

.

Dacă această limită există și este egală cu un anumit număr, și nu cu infinit, atunci integrala improprie se numește convergentă, iar numărul egal cu limita este luat ca valoare. In caz contrar integrala improprie se numește divergentăși nu i se atribuie nicio valoare.

Exemplul 1. Calculați integrala improprie(dacă converge).

Soluţie. Pe baza definiției integralei improprie, găsim

Deoarece limita există și este egală cu 1, atunci dat integrala improprie converge si este egal cu 1.

În exemplul următor, integrandul este aproape același ca în exemplul 1, doar că gradul lui x nu este doi, ci litera alfa, iar sarcina este de a studia integrala improprie pentru convergență. Adică, întrebarea rămâne de răspuns: la ce valori ale alfa converge această integrală necorespunzătoare și la ce valori diverge?

Exemplul 2. Investigați convergența unei integrale improprie(limita inferioară de integrare este mai mare decât zero).

Soluţie. Să presupunem mai întâi că, apoi

În expresia rezultată, trecem la limita de la:

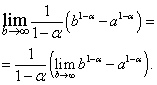
Este ușor de observat că limita din partea dreaptă există și este egală cu zero atunci când , adică , și nu există când , adică .

În primul caz, adică atunci când . Daca atunci si nu exista.

Concluzia studiului nostru este următoarea: integrala improprie converge la şi diverge la .

Aplicând la tipul studiat de integrală improprie formula Newton-Leibniz , putem deriva următoarea formulă foarte asemănătoare:

.

Aceasta este formula generalizată Newton-Leibniz.

Exemplul 3. Calculați integrala improprie(dacă converge).

Limita acestei integrale există:

A doua integrală, care este suma care exprimă integrala inițială:

Limita acestei integrale există și:

.

Găsim suma a două integrale, care este și valoarea integralei improprie originale cu două limite infinite:

Integrale improprii de al doilea fel - din funcții nemărginite și convergența lor

Lasă funcția f(X) stabilite pe segmentul din A inainte de b și nelimitat pe ea. Să presupunem că funcția merge la infinit în punctul respectiv b , în timp ce în toate celelalte puncte ale segmentului este continuă.

Definiție. Integrală improprie a funcției f(X) pe segmentul de la A inainte de b se numeste limita integralei acestei functii cu limita superioara a integrarii c , dacă atunci când te străduiești c La b funcția crește la nesfârșit și la punct X = b funcția nu este definită, adică

.

Dacă această limită există, atunci integrala improprie de al doilea fel se numește convergentă, altfel divergentă.

Folosind formula Newton-Leibniz, derivăm.

Exemple de studiere a integralelor improprii pentru convergență

Exemplul 1
.

Astfel, această integrală converge pentru a > 1 și diverge pentru a £ 1.

Exemplul 2 Investigați pentru convergență. Calculăm integrala prin definiție:
.

Astfel, această integrală converge pentru a<1 и расходится при a³1.

Exemplul 3 Investigați pentru convergență .

<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два

.

Studiem convergența primei integrale I1 folosind o funcție echivalentă: (pentru că n>0), iar integrala converge când m>-1 (exemplul 2). În mod similar, pentru integrala I2:

Și integrala converge pentru m+n<-1 (пример2). Следовательно, исходный интеграл сходится при выполнении одновременно двух условий m>-1 și m+n<-1, и будет расходится при нарушении хотя бы одного из них.

Exemplul 4 Investigați pentru convergență.

Integrandul poate fi infinit de mare (dacă m<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два:

Deoarece arctgx »x la x®0, atunci integrala I1 este echivalentă cu integrala , care converge pentru m+1>-1, adică pentru m>-2 (exemplul 1).

Pentru integrandul din integrala improprie de primul fel I2, alegem unul echivalent:

întrucât arctgx » p/2 pentru x® ¥. Prin urmare, conform celui de-al doilea criteriu de comparație, integrala I2 va converge pentru m + n<-1, и расходится в противном случае.

Combinând condițiile de convergență a integralelor I1 și I2, obținem condițiile de convergență a integralei originale: m>-2 și m+n<-1 одновременно.

Cometariu.În exemplele 2-4 s-a folosit un criteriu de comparație 2, care asigură condițiile necesare și suficiente pentru convergență, care permite, prin stabilirea convergenței într-o anumită condiție asupra valorilor parametrilor, să nu se dovedească divergența integralei. dacă sunt încălcate condiţiile de convergenţă obţinute.

Exemplul 5 Investigați pentru convergență.

Această integrală conține un punct singular 0, la care integrandul poate deveni infinit pentru p<0, поэтому снова разобьем исходный интеграл на два:

.

Integrala I1 este o integrală improprie de al doilea fel, iar integrandul este echivalent la x®0 cu funcția xp (e-x®1 la x®0), adică I1 converge pentru p>-1 (Exemplul 1).

Integrala I2 este o integrală improprie de primul fel. Alegeți o funcție echivalentă cu integrand, astfel încât să nu conțină o funcție exponențială, eșuează. Prin urmare, este imposibil să se utilizeze criteriul de comparație 2, ca în exemplele anterioare. Să aplicăm primul semn de comparație, pentru care folosim următorul fapt bine-cunoscut:

Pentru a>0 și orice p. De aici și de faptul că funcția xpe-ax este continuă, rezultă că această funcție este mărginită, adică există o constantă M>0 astfel încât xpe-ax< M. Возьмем, например, a=1/2, и оценим интеграл I2 сверху:

Adică, integrala I2 converge pentru orice p.

Astfel, integrala originală converge pentru p>-1.

Exemplul 6 Investigați pentru convergență.

Să schimbăm variabila: t = lnx și să obținem

Împărțirea integralei în două se realizează în mod similar cu exemplul 5. Integrala I1 este complet echivalentă cu integrala I1 din exemplul 5 și, prin urmare, converge pentru q<1.

Se consideră integrala I2 . Sub rezerva 1-p<0 этот интеграл полностью эквивалентен интегралу I2 в примере 5 (доказательство сходимости аналогично, а условие 1-p<0 нужно для выполнения și a=(1-p)/2.).

Deci, I2 converge pentru p>1. Totuși, acest studiu al convergenței acestei integrale nu este finalizat, deoarece criteriul de convergență utilizat oferă doar condiții suficiente pentru convergență. Prin urmare, este necesar un studiu al convergenței ca 1-p £ 0.

Se consideră cazul p=1. Atunci integrala I2 este echivalentă cu , care converge pentru q>1 (rețineți că integrala I1 diverge în acest caz) și diverge altfel.

Pentru p<1 оценим интеграл I2 и покажем его расходимость. Для этого вспомним, что Pentru 1-p>0 și, prin urmare, pornind de la niște A>1, T- QE(1- P) T³M=const>0. Atunci integrala I2 satisface estimarea

,

Unde integrala din partea dreaptă diverge, ceea ce demonstrează divergența integralei I2 .

Însumând rezultatele obținute, obținem că integrala inițială converge pentru q<1 и p>1, altfel integrala diverge.

Exemplul 6 Examinați convergența absolută și condiționată.

Să despărțim integrala originală în două:

.

Convergenţă. Integrala I1 este echivalentă cu , adică converge pentru p<2 (пример 1) , причем абсолютно, так как подынтегральная функция положительна на отрезке интегрирования.

Integrala I2 converge în jurul criteriului Dirichlet-Abel pentru p>0, deoarece antiderivata sin(x) este mărginită, iar funcția 1/xp tinde monoton către zero pe măsură ce x tinde spre infinit.

Să arătăm că pentru p £ 0 integrala diverge. Pentru aceasta folosim criteriul Cauchy, sau mai degrabă negația lui

.

Să luăm următoarele valori ca R1 și R2: R1=2pk și R2=2pk+p/2, apoi

, pentru p>0.

Astfel, integrala converge la 0

Convergență absolută Convergența absolută a integralei I1 a fost deja stabilită, să considerăm convergența absolută a lui I2 . Să estimăm integrala de mai sus:

, adică integrala converge pentru p>1.

Pentru a demonstra divergența pentru p £ 1, estimăm integrala de jos

.

Împărțim ultima integrală a diferenței de funcții în diferența de integrale

.

Dacă ambele integrale converg, atunci integrala diferenței converge; dacă una dintre integrale diverge și cealaltă converge, atunci integrala diferenței diverge. În cazul divergenței ambelor integrale, convergența integralei diferenței este supusă investigațiilor ulterioare. Ne interesează al doilea dintre cazurile descrise.

Divergent (exemplul 1) la p<1. сходится по признаку Дирихле-Абеля при 1>p>0 (vezi Convergență), prin urmare integrala este estimată de jos printr-o integrală divergentă, adică diverge.

Cazul p³1 nu ne interesează, deoarece integrala diverge pentru aceste valori ale parametrului.

Astfel, integrala inițială converge absolut la 0

Dacă integrandul are o discontinuitate de al doilea fel pe intervalul (finit) de integrare, se vorbește de o integrală improprie de al doilea fel.

10.2.1 Definiție și proprietăți de bază

Să notăm intervalul de integrare $\left[ a, \, b \right ]$, ambele numere se presupune că sunt finite mai jos. Dacă există doar 1 decalaj, acesta poate fi fie în punctul $a$, fie în punctul $b$, fie în interiorul intervalului $(a,\,b)$. Să luăm mai întâi în considerare cazul când există o discontinuitate de al doilea fel în punctul $a$, iar integrandul este continuu în alte puncte. Deci discutăm despre integrală

\begin(equation) I=\int _a^b f(x)\,dx, (22) \label(intr2) \end(equation)

unde $f(x) \rightarrow \infty $ când $x \rightarrow a+0$. Ca și înainte, primul lucru de făcut este să dai sens acestei expresii. Pentru a face acest lucru, luați în considerare integrala

\[ I(\epsilon)=\int _(a+\epsilon)^b f(x)\,dx. \]

Definiție. Să existe o limită

\[ A=\lim _(\epsilon \rightarrow +0)I(\epsilon)=\lim _(\epsilon \rightarrow +0)\int _(a+\epsilon)^b f(x)\,dx. \]

Atunci se spune că integrala improprie de al doilea fel (22) converge și i se atribuie valoarea $A$, funcția $f(x)$ însăși se spune că este integrabilă pe intervalul $\left[ a, \ , b\dreapta]$.

Să considerăm varianta când există o discontinuitate a celui de-al doilea fel de integrand la limita superioară a intervalului de integrare. Acest caz poate fi redus la cel anterior prin modificarea variabilei $x=-t$ și apoi rearanjarea limitelor de integrare.

Să considerăm cazul în care integrandul are o discontinuitate de al doilea fel în interiorul intervalului de integrare, în punctul $c \in (a,\,b)$. În acest caz, integrala originală

\begin(equation) I=\int _a^bf(x)\,dx (23) \label(intr3) \end(equation)

prezentat ca o sumă

\[ I=I_1+I_2, \quad I_1=\int _a^cf(x)\,dx +\int _c^df(x)\,dx. \]

Definiție. Dacă ambele integrale $I_1, \, I_2$ converg, atunci integrala improprie (23) se numește convergentă și i se atribuie o valoare egală cu suma integralelor $I_1, \, I_2$, funcției $f(x) $ se numește integrabil pe intervalul $\left [a, \, b\right]$. Dacă cel puţin una dintre integralele $I_1,\, I_2$ este divergentă, se spune că integrala improprie (23) este divergentă.

Integralele improprie convergente de al 2-lea fel au toate proprietățile standard ale integralelor definite obișnuite.

1. Dacă $f(x)$, $g(x)$ sunt integrabile pe intervalul $\left[ a, \,b \right ]$, atunci suma lor $f(x)+g(x)$ este de asemenea, integrabil în acest interval și \[ \int _a^(b)\left(f(x)+g(x)\right)dx=\int _a^(b)f(x)dx+\int _a^( b)g (x)dx. \] 2. Dacă $f(x)$ este integrabil pe intervalul $\left[ a, \, b \right ]$, atunci pentru orice constantă $C$ funcția $C\cdot f(x)$ este de asemenea integrabil pe acest interval , și \[ \int _a^(b)C\cdot f(x)dx=C \cdot \int _a^(b)f(x)dx. \] 3. Dacă $f(x)$ este integrabil pe intervalul $\left[ a, \, b \right ]$ și $f(x)>0$ pe acest interval, atunci \[ \int _a^( b ) f(x)dx\,>\,0. \] 4. Dacă $f(x)$ este integrabil pe intervalul $\left[ a, \, b \right ]$, atunci pentru orice $c\in (a, \,b)$ integralele \[ \ int _a^ (c) f(x)dx, \quad \int _c^(b) f(x)dx \] converg, de asemenea, și \[ \int _a^(b)f(x)dx=\int _a ^(c ) f(x)dx+\int _c^(b) f(x)dx \] (aditivitatea integralei pe interval).

Luați în considerare integrala

\begin(equation) I=\int _0^(1)\frac(1)(x^k)\,dx. (24) \label(mod2) \end(equation)

Dacă $k>0$, integrandul tinde spre $\infty$ ca $x \rightarrow +0$, deci integrala este improprie de al doilea fel. Vă prezentăm funcția

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx. \]

În acest caz, antiderivatul este cunoscut, astfel încât

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k )|_(\epsilon)^1= \frac(1)(1-k)-\frac(\epsilon ^(1-k))(1-k). \]

pentru $k \neq 1$,

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x)\,dx\,=lnx|_(\epsilon)^1= -ln \epsilon. \]

pentru $k = 1$. Având în vedere comportamentul pentru $\epsilon \rightarrow +0$, concluzionăm că integrala (20) converge pentru $k

10.2.2 Criterii de convergență a integralelor improprie de al 2-lea fel

Teorema (primul semn al comparației). Fie $f(x)$, $g(x)$ continuu pentru $x\in (a,\,b)$ și $0 1. Dacă integrala \[ \int _a^(b)g(x) dx \] converge, atunci converge și integrala \[ \int _a^(b)f(x)dx. \] 2. Dacă integrala \[ \int _a^(b)f(x)dx \] diverge, atunci diverge și integrala \[ \int _a^(b)g(x)dx. \]

Teorema (al doilea semn de comparație). Fie $f(x)$, $g(x)$ continuu și pozitiv pentru $x\in (a,\,b)$ și să existe o limită finită

\[ \theta = \lim_(x \rightarrow a+0) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \]

Apoi integralele

\[ \int _a^(b)f(x)dx, \quad \int _a^(b)g(x)dx \]

converg sau diverg în acelaşi timp.

1. Integrale improprii cu limite infinite

Reamintim definiția unei integrale ca limită a sumelor integrale:

Definiția presupune că intervalul de integrare este finit, iar funcția f (x) este continuă în el. Încălcarea acestor ipoteze duce la integrale necorespunzătoare.

Definiție. Dacă integrala tinde către o limită finită cu o creștere nelimitată "b", atunci această limită se numește integrală improprie cu o limită superioară infinită a funcției f (x) și se notează cu simbolul

În acest caz, se spune că integrala improprie există sau converge.

Dacă limita specificată nu există sau există, dar este infinită, atunci se spune că integrala nu există sau diverge.

Integrala improprie cu limita inferioară infinită este definită în mod similar:

O integrală improprie cu două limite infinite este definită prin formula:

unde c este orice punct fix pe axa x.

Deci, integralele improprie pot fi cu o limită infinit inferioară, cu o limită infinit superioară și, de asemenea, cu două limite infinite.

Semne de convergență. Convergența absolută și condiționată

Integrala există numai atunci când fiecare dintre integrale există: și .

Exemplu. Investigați convergența integralei

Presupunând c = 0, obținem:

acestea. integrala converge.

Uneori nu este nevoie să se calculeze integrala improprie, dar este suficient să știm dacă converge sau diverge comparând-o cu o altă integrală.

O teoremă de comparație pentru integrale improprie.

Fie ca funcția f (x) să aibă mai multe (număr finit) puncte de discontinuitate de primul fel în interval, acest „obstacol” poate fi ușor eliminat prin împărțirea segmentului cu puncte de discontinuitate în mai multe segmente, calculați integralele definite pe fiecare secțiune separată și adăugați rezultatele.

Considera integrala definita dintr-o funcție care este nemărginită atunci când se apropie de unul dintre capetele segmentului, de exemplu, .

(În astfel de cazuri, se spune de obicei: „Funcția are o discontinuitate infinită la capătul din dreapta al segmentului de integrare”.)

Este clar că definiția obișnuită a integralei își pierde aici sensul.

Definiție. Integrala improprie a funcției f(x), care este continuă pentru un £ x< b и неограниченной при x ® b - 0, называется предел:

În mod similar, integrala improprie a unei funcții care are o discontinuitate infinită la capătul din stânga intervalului este definită:

Prin urmare, în zona [ -1, 0] integrala diverge.

Aceasta înseamnă că integrala diverge și pe segment.

Astfel, această integrală diverge pe întregul segment [-1, 1]. Rețineți că dacă am începe să calculăm această integrală, fără a acorda atenție discontinuității integrandului în punctul x = 0, am obține un rezultat incorect. Într-adevăr,

, ceea ce este imposibil.

Deci, pentru a studia integrala improprie a unei funcții discontinue, este necesar să o „rupem” în mai multe integrale și să le investighezi.