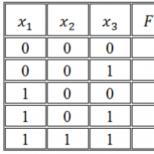
Diskreetin matematiikan oppikirja dnf, sdnf, knf, sknf. Boolen funktioiden erikoisesitykset loogisen funktion konjunktiivisella normaalimuodolla
Mille tahansa loogiselle kaavalle identiteettimuunnoksia käyttämällä voidaan rakentaa äärettömän monta sitä vastaavia kaavoja. Logiikkaalgebrassa yksi päätehtävistä on kanonisten muotojen (eli yhden säännön, kaanonin) mukaan rakennettujen kaavojen etsiminen.
Jos looginen funktio ilmaistaan muuttujien disjunktiolla, konjunktiolla ja negaatiolla, tätä esitysmuotoa kutsutaan normaaliksi.
Normaalimuodoista erotetaan täydelliset normaalimuodot (ne muodot, joissa funktiot kirjoitetaan ainutlaatuisella tavalla).
Täydellinen disjunktiivinen normaalimuoto (PDNF)
Määritelmä. Kaavaa kutsutaan alkeiskonjunktioksi, jos se muodostuu tietyn määrän muuttujia tai niiden negaatioita konjunktiosta.
Esimerkkejä: y, ¬ y, x 1 ∧ ¬ x 2 ∧ x 3 ∧ x 4
Määritelmä. Kaavaa kutsutaan disjunktiiviseksi normaalimuodoksi (DNF), jos se on ei-toistuvien alkeiskonjunktioiden disjunktio.
DNF kirjoitetaan seuraavassa muodossa: F 1 ∨ F 2 ∨ ... ∨ F n , missä F i on alkeiskonjunktio
Esimerkkejä: ¬ x 1 ∧ x 2 ∨ x 1 ∧ ¬ x 2 ∨ x 1 ∧ ¬ x 2 ∧ x 3, ¬ y 1 ∨ y 1 ∧ y 2 ∨ ¬ y 2
Määritelmä. K muuttujan loogista kaavaa kutsutaan täydelliseksi disjunktiiviseksi normaalimuodoksi (PDNF), jos:
1) kaava on DNF, jossa jokainen alkeiskonjunktio on k muuttujan x 1, x 2, ..., x k konjunktio ja tämän konjunktion i:nnessä paikassa on joko muuttuja x i tai sen negaatio ;
2) kaikki tällaisen DNF:n alkeiskonjunktiot ovat pareittain erillisiä.
Esimerkki: (¬ x 1 ∧ x 2 ∧ x 3) ∨ (x 1 ∧ ¬ x 2 ∧ x 3) ∨ (x 1 ∧ x 2 ∧ ¬ x 3)
Täydellinen konjunktiivinen normaalimuoto (PCNF)
Määritelmä. Kaavaa kutsutaan alkeisdisjunktioksi, jos se muodostuu tietyn määrän muuttujia tai niiden negaatioita disjunktiosta.
Esimerkkejä: ¬ x 3, x 1 ∨ x 2, x 1 ∨ x 2 ∨ ¬ x 3
Määritelmä. Kaavaa kutsutaan konjunktiiviseksi normaalimuodoksi (CNF), jos se on ei-toistuvien alkeisdisjunktioiden konjunktio.
CNF kirjoitetaan seuraavassa muodossa: F 1 ∧ F 2 ∧ ... ∧ F n , jossa F i on alkeisdisjunktio
Esimerkkejä: (x 1 ∨ ¬ x 2) ∧ x 3, (x 1 ∨ x 2) ∧ (¬ x 1 ∨ x 2 ∨ x 3) ∧ (x 1 ∨ ¬ x 2 ∨ ¬ x 3)
Määritelmä. K muuttujan loogista kaavaa kutsutaan täydelliseksi konjunktiiviseksi normaalimuodoksi (CPNF), jos:
1) kaava on CNF, jossa jokainen alkeisdisjunktio on k muuttujan x 1, x 2, ..., x k disjunktio ja tämän disjunktion i:nnessä paikassa on joko muuttuja x i tai sen negaatio;
2) kaikki alkeisdisjunktiot sellaisessa CNF:ssä ovat pareittain erillisiä.
Esimerkki: (x 1 ∨ x 2 ∨ x 3) ∧ (¬ x 1 ∨ ¬ x 2 ∨ x 3)
huomaa, että mikä tahansa looginen funktio, joka ei ole sama kuin 0 tai 1, voidaan esittää SDNF- tai SKNF-muodossa.
Algoritmi SDNF:n muodostamiseksi totuustaulukon avulla
- Valitse kaikki taulukon rivit, joissa funktion arvo on yhtä suuri kuin yksi.
- Kirjoita jokaiselle tällaiselle riville kaikkien muuttujien konjunktio seuraavasti: jos jonkin muuttujan arvo tässä joukossa on 1, sisällytetään konjunktioon itse muuttuja, muuten sen negaatio.
- Yhdistämme kaikki tuloksena saadut konjunktiot disjunktiooperaatioilla.
Algoritmi SCNF:n muodostamiseksi totuustaulukon avulla
- Valitse kaikki taulukon rivit, joissa funktion arvo on nolla.
- Kirjoita kullekin sellaiselle riville kaikkien muuttujien disjunktio seuraavasti: jos jonkin muuttujan arvo tässä joukossa on 0, sisällytetään konjunktioon itse muuttuja, muuten sen negaatio.
- Yhdistämme kaikki tuloksena olevat disjunktiot konjunktiooperaatioilla.
Algoritmien analyysi osoittaa, että jos suurimmalla osalla totuustaulukon riveistä funktion arvo on 0, niin sen loogisen kaavan saamiseksi on parempi rakentaa SDNF, muuten - SCNF.
Esimerkki: On annettu kolmen muuttujan loogisen funktion totuustaulukko. Muodosta looginen kaava, joka toteuttaa tämän funktion.
| x | y | z | F(x, y, z) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Koska Useimmilla totuustaulukon riveillä funktion arvo on 1, niin rakennetaan SCNF. Tuloksena saamme seuraavan loogisen kaavan:
F = (¬ x ∨ y ∨ z) ∧ (¬ x ∨ y ∨ ¬ z)
Tarkastetaan tuloksena oleva kaava. Tätä varten rakennamme funktion totuustaulukon.
| x | y | z | ¬x | ¬ x ∨ y ∨ z | ¬z | ¬ x ∨ y ∨ ¬ z | F(x, y, z) |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
Vertaamalla alkuperäistä totuustaulukkoa ja loogiselle kaavalle rakennettua totuustaulukkoa huomaamme, että funktioarvojen sarakkeet ovat samat. Tämä tarkoittaa, että looginen funktio on rakennettu oikein.
Propositialgebran disjunktiiviset ja konjunktiiviset normaalimuodot. Jokaiselle lauselogiikkafunktiolle voidaan rakentaa totuustaulukko. Käänteinen ongelma on myös aina ratkaistavissa. Otetaan käyttöön useita määritelmiä.
Elementaariset konjunktiot (konjunktiot) kutsutaan muuttujien konjunktioiksi tai niiden negaatioiksi, joissa kukin muuttuja esiintyy enintään
kerran.
Disjunktiivinen normaalimuoto(DNF) on kaava, joka on muodoltaan alkeiskonjunktioiden disjunktio.
Elementaariset disjunktiot (disjunktiot) kutsutaan muuttujien disjunktioiksi negaatioiden kanssa tai ilman.
Konjunktiivinen normaalimuoto(CNF) on kaava, jolla on alkeisdisjunktioiden konjunktio.
Jokaiselle lausealgebrafunktiolle voidaan löytää joukko disjunktiivisia ja konjunktiivisia normaalimuotoja.
Algoritmi DNF:n muodostamiseksi:
1. Siirry Boolen toimintoihin käyttämällä vastaavia muunnoskaavoja.
2. Siirry kaavoihin, joissa on läheisiä negaatioita, eli kaavaan, jossa negaatiot eivät sijaitse korkeintaan muuttujien yläpuolella - noudata De Morganin lakeja.
3. Avaa sulut - noudata jakautumislakeja.
4. Otetaan toistuvat termit yksi kerrallaan - idempotenssin laki.
5. Käytä absorption ja puoliabsorption lakeja.
Esimerkki 6. Etsi DNF-kaavat: .
Boolen algebrassa se on totta kaksinaisuuden periaate. Se on seuraava.
Funktiota kutsutaan kaksinkertainen toimintoon if . Nuo. Jotta löydettäisiin funktio, joka on duaalinen tietylle funktiolle, on välttämätöntä rakentaa funktion negaatio argumenttien negaatioista.
Esimerkki 7. Etsi funktio dual to .
Logiikkaalgebran perusfunktioista 1 on duaali 0:aan ja päinvastoin, x on duaali x:ään, duaali , duaaliin ja päinvastoin.
Jos funktiota edustavassa kaavassa F 1 korvataan kaikki konjunktiot
disjunktiossa, disjunktio konjunktiossa, 1 0:ssa, 0 1:ssä, niin saadaan kaava F *, joka edustaa funktiota * dual to .
Konjunktiivinen normaalimuoto (CNF) on kaksikonsepti DNF:lle, joten se voidaan helposti rakentaa seuraavan kaavion mukaisesti:
Esimerkki 8. Etsi CNF-kaava: .
Käytämme esimerkin 6 tulosta
Täydelliset disjunktiiviset ja täydelliset konjunktiiviset normaalimuodot. Jokaisessa normaalimuototyypissä (disjunktiivinen ja konjunktiivinen) voidaan erottaa täydellinen muotojen luokka SDNF ja SCNF.
Täydellinen alkeiskonjunktio on kaikkien muuttujien looginen tulo negaatiolla tai ilman, ja jokainen muuttuja esiintyy tulossa vain kerran.
Mikä tahansa DNF voidaan pelkistää SDNF:ksi jakamalla konjunktiot, jotka eivät sisällä kaikkia muuttujia, ts. lisäämällä puuttuvan muuttujan x i kerrotaan distributiivisen lain avulla
Esimerkki 9. Etsi SDNF esimerkin 6 DNF:lle
Täydellinen alkeisdisjunktio on kaikkien muuttujien looginen summa negaatioilla tai ilman, ja jokainen muuttuja sisältyy summaan vain kerran.
Mikä tahansa CNF voidaan pelkistää SCNF:ksi lisäämällä konjunktiossa konjunktiotermi, joka ei sisällä muuttujaa X i, ja soveltamalla distributiivista lakia
Esimerkki 10. Tuo KNF SKNF:lle:
SCNF:n rakentamiseen voit käyttää kaaviota
Esimerkki 11. Etsi esimerkin 6 kaavan SCNF.
Jokaisella toiminnolla on SDNF ja lisäksi ainutlaatuinen. Jokaisella toiminnolla on SCNF ja lisäksi ainutlaatuinen.
Koska SDNF ja SKNF määritellään yksiselitteisesti kaavoilla; ne voidaan rakentaa käyttämällä kaavan totuustaulukkoa.
SDNF:n muodostamiseksi on tarpeen valita rivit, joissa F saa arvon 1, ja kirjoittaa niille täydelliset alkeiskonjunktiot. Jos muuttujan arvo totuustaulukon halutulla rivillä on yhtä suuri kuin yksi, niin täydellisessä konjunktiossa se otetaan ilman negaatiota, jos nolla, niin negaatiolla. Sitten täydelliset konjunktiot (niiden lukumäärä on yhtä suuri kuin taulukon yksiköiden lukumäärä) yhdistetään disjunktiomerkeillä.
SCNF:n rakentamiseksi totuustaulukon avulla on tarpeen valita siitä rivit, joissa F = 0, ja kirjoittaa täydelliset alkeisdisjunktiot ja yhdistää ne sitten konjunktiomerkeillä. Jos totuustaulukon vaaditulla rivillä (F=0) muuttujan arvo vastaa nollaa, niin täydellisessä lauseessa se otetaan ilman negaatiota, jos se on yksi, niin negaatiolla.
Esimerkki 12. Etsi SDNF ja SCNF käyttämällä esimerkin 6 kaavan totuustaulukkoa.
Taulukko 14 näyttää vain lopullisen arvon F=10101101. Sinun tulee itse varmistaa tämän väitteen paikkansapitävyys rakentamalla yksityiskohtainen totuustaulukko.
Taulukko 14
| x | y | z | ||
Yksinkertainen disjunktio(eng. inclusive disjunktion) tai disjunktio(englanniksi disjunct) on yhden tai useamman muuttujan tai niiden negaatioiden disjunktio, jossa jokainen muuttuja esiintyy enintään kerran.
Yksinkertainen disjunktio
- koko, jos jokainen muuttuja (tai sen negaatio) esiintyy täsmälleen kerran;
- yksitoikkoinen, jos se ei sisällä muuttujien negaatioita.
Konjunktiivinen normaalimuoto, CNF(eng. konjunktiivinen normaalimuoto, CNF) normaalimuoto, jossa Boolen funktiolla on useiden yksinkertaisten lauseiden konjunktio.
CNF esimerkki:$f(x,y) = (x \lor y) \land (y \lor \neg ( z ))$
SKNF
Täydellinen konjunktiivinen normaalimuoto, SCNF(englanniksi täydellinen konjunktiivinen normaalimuoto, PCNF) on CNF, joka täyttää ehdot:
- se ei sisällä identtisiä yksinkertaisia disjunktioita
- jokainen yksinkertainen disjunktio on valmis
SKNF esimerkki:$f(x,y,z) = (x \lor \neg ( y ) \lor z) \land (x\lor y \lor \neg ( z ))$
Lause: Jokaiselle Boolen funktiolle $f(\vec ( x ))$, joka ei ole sama kuin identiteetti, on olemassa SCNF, joka määrittää sen.
Todiste: Koska funktion $\neg ( f ) (\vec x)$ käänteisarvo on yhtä suuri kuin yksi niissä joukoissa, joissa $f(\vec x)$ on nolla, niin $\neg ( f ) SDNF (\vec x)$ voidaan kirjoittaa seuraavasti:
$\neg ( f ) (\vec x) = \bigvee\limits_ ( f(x^ ( \sigma_ ( 1 ) ) , x^ ( \sigma_ ( 2 ) ), ... ,x^ ( \sigma_ ( n ) ) )) = 0 ) (x_ ( 1 ) ^ ( \sigma_ ( 1 ) ) \wedge x_ ( 2 ) ^ ( \sigma_ ( 2 ) ) \wedge ... \wedge x_ ( n ) ^ ( \sigma_ ( n ) ) )) $, jossa $ \sigma_ ( i ) $ tarkoittaa negatiivisen olemassaoloa tai puuttumista kohdassa $ x_ ( i ) $
Etsitään lausekkeen vasemman ja oikean puolen käännös:
$ f(\vec x) = \neg (( \bigvee\limits_ ( f(x^ ( \sigma_ ( 1 ) ) ), x^ ( \sigma_ ( 2 ) ), ... ,x^ ( \sigma_ ( n ) )) = 0 ) (x_ ( 1 ) ^ ( \sigma_ ( 1 ) ) \wedge x_ ( 2 ) ^ ( \sigma_ ( 2 ) ) \wedge ... \wedge x_ ( n ) ^ ( \sigma_ ( n ) ) )) )) $
Kun de Morganin sääntöä sovelletaan kahdesti oikealla puolella saatuun lausekkeeseen, saadaan: $ f(\vec x) = \bigwedge \limits_ ( f(x^ ( \sigma_1 ) , x^ ( \sigma_2 ) , \dots ,x ^ ( \ sigma_n )) = 0 ) $ $(\neg ( x_1^ ( \sigma_1 ) ) \vee \neg ( x_2^ ( \sigma_2 ) ) \vee \dots \vee \neg ( x_n^ ( \sigma_n ) ) ) $
Viimeinen lauseke on SKNF. Koska SCNF saadaan SDNF:stä, joka voidaan konstruoida mille tahansa funktiolle, joka ei ole identtinen nolla, lause on todistettu.
Algoritmi SCNF:n muodostamiseksi totuustaulukon avulla
- Totuustaulukkoon merkitään ne muuttujajoukot, joille funktion arvo on $0$.
- Jokaiselle merkitylle joukolle kirjoitetaan kaikkien muuttujien disjunktio seuraavan säännön mukaan: jos jonkin muuttujan arvo on $0$, sisällytetään disjunktioon itse muuttuja, muuten sen negaatio.
- Yhdistämme kaikki tuloksena olevat disjunktiot konjunktiooperaatioilla.
Esimerkki SCNF:n rakentamisesta mediaanille
1). Totuustaulukkoon merkitään ne muuttujajoukot, joille funktion arvo on $0$.
| x | y | z | $ \langle x,y,z \rangle $ |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
2). Jokaiselle merkitylle joukolle kirjoitetaan kaikkien muuttujien konjunktio seuraavan säännön mukaan: jos jonkin muuttujan arvo on $0$, sisällytetään disjunktioon itse muuttuja, muuten sen negaatio.
| x | y | z | $ \langle x,y,z \rangle $ | |
| 0 | 0 | 0 | 0 | $(x \lor y \lor z)$ |
| 0 | 0 | 1 | 0 | $(x \lor y \lor \neg ( z ))$ |
| 0 | 1 | 0 | 0 | $(x \tai \neg ( y ) \tai z)$ |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | $(\neg ( x ) \tai y \tai z)$ |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 |
3). Yhdistämme kaikki tuloksena olevat disjunktiot konjunktiooperaatioilla.
$ \langle x,y,z \rangle = (x \lor y \lor z) \land (\neg ( x ) \lor y \lor z) \land (x \lor \neg ( y ) \lor z) \maa (x \lor y \lor \neg ( z ))$
Esimerkkejä SKNF:stä joillekin toiminnoille
Peircen nuoli: $ x \downarrow y = (\neg ( x ) \lor ( y )) \land (( x ) \lor \neg ( y )) \land (\neg ( x ) \lor \neg ( y ) ) $
Yksinomainen tai: $ x \oplus y \oplus z = (\neg ( x ) \lor \neg ( y ) \lor z) \land (\neg ( x ) \lor y \lor \neg ( z )) \maa (x \lor \neg ( y ) \lor \neg ( z )) \land (x \lor y \lor z)$
Normaali muoto looginen kaava ei sisällä merkkejä ei-alkeiskaavojen implikaatiosta, ekvivalenssista ja negaatiosta.
Normaalimuotoa on kahdessa muodossa:
konjunktiivinen normaalimuoto (CNF)-- useiden disjunktioiden konjunktio, esimerkiksi $\left(A\vee \overline(B)\vee C\right)\wedge \left(A\vee C\oikea)$;
disjunktiivinen normaalimuoto (DNF)-- useiden konjunktioiden disjunktio, esimerkiksi $\left(A\wedge \overline(B)\wedge C\right)\vee \left(B\wedge C\right)$.
SKNF
Täydellinen konjunktiivinen normaalimuoto (PCNF) on CNF, joka täyttää kolme ehtoa:
ei sisällä identtisiä alkeisdisjunktioita;
mikään disjunktioista ei sisällä samoja muuttujia;
jokainen alkeisdisjunktio sisältää jokaisen muuttujan, joka sisältyy tiettyyn CNF:ään.
Mikä tahansa Boolen kaava, joka ei ole täysin totta, voidaan esittää SKNF:ssä.
Säännöt SKNF:n rakentamiseen totuustaulukon avulla
Jokaiselle muuttujajoukolle, jonka funktio on yhtä suuri kuin 0, summa kirjoitetaan ylös ja muuttujat, joiden arvo on 1, otetaan negaatiolla.
SDNF
Täydellinen disjunktiivinen normaalimuoto (PDNF) on DNF, joka täyttää kolme ehtoa:
ei sisällä identtisiä alkeiskonjunktioita;
mikään konjunktioista ei sisällä samoja muuttujia;
Jokainen alkeiskonjunktio sisältää kaikki tiettyyn DNF:ään sisältyvät muuttujat samassa järjestyksessä.
Mikä tahansa Boolen kaava, joka ei ole identtisesti epätosi, voidaan esittää SDNF:ssä ja ainutlaatuisella tavalla.
Säännöt SDNF:n rakentamiseen totuustaulukon avulla
Jokaiselle muuttujajoukolle, jonka funktio on yhtä suuri kuin 1, kirjoitetaan tulo, ja muuttujat, joiden arvo on 0, otetaan negatiivisesti.
Esimerkkejä SCNF:n ja SDNF:n löytämisestä
Esimerkki 1
Kirjoita looginen funktio käyttämällä sen totuustaulukkoa:
Kuva 1.
Ratkaisu:
Käytämme sääntöä SDNF:n rakentamiseen:

Kuva 2.
Saamme SDNF:n:
Käytetään sääntöä SCNF:n rakentamiseen.
Esimerkki. Etsi CNF-kaavat ![]()
~ ![]() ~
~
![]()
SDNF:n täydellinen disjunktiivinen normaalimuoto voidaan rakentaa käyttämällä seuraavaa algoritmia:
1. = 1. DNF-algoritmi
2. = 2. DNF-algoritmi
3. = 3. DNF-algoritmi
4. = 4. DNF-algoritmi
5. Jätä pois identtiset väärät termit, eli lomakkeen termit
6. Täydennä loput termit puuttuvilla muuttujilla
7. Toista kohta 4.
Esimerkki. Etsi SDNF-kaavat.
![]() ~
~
![]()
![]()
![]()
![]()
SCNF:n rakentamiseen voit käyttää seuraavaa kaaviota:
Esimerkki. Etsi SDNF-kaavat.
![]() ~
~
![]()
Tiedetään (Lauseet 2.11, 2.12), että SDNF ja SCNF määritellään yksiselitteisesti kaavalla ja siksi ne voidaan konstruoida käyttämällä kaavan totuustaulukkoa.
Kaava SDNF:n ja SCNF:n rakentamiseksi totuustaulukon mukaan on annettu alla kaavalle ![]() ~ :
~ :
| | ||||
| 1 0 1 0 1 1 0 1 | SDNF; SKNF. |
2.2. Harjoittele.
2.2.1 Alla on Boolen lausekkeet. Yksinkertaista muunnelmasi lausekkeet mahdollisimman paljon käyttämällä Boolen logiikan lakeja. Käytä sitten totuustaulukoita vertaillaksesi yksinkertaistettua lausekettasi alkuperäiseen.






2.2.2. Selvitä kysymys f 1:n ja f 2:n vastaavuudesta vähentämällä ne SDNF:ksi (taulukko 1).
2.2.3. Etsi f 3:n kaksoisfunktio käyttämällä yleistettyä ja Boolen periaatetta (taulukko 1). Vertaa tuloksia.
| № | f 1 | f 2 | f 3 |
| | |||
| |
|||
| | |||
| | |||
| | |||
| | |
||
| | |
||
| |
|||
| | |||
| | |||
| |
|||
| | |||
| | |
||
| | |||
| |
2.3. Kontrollikysymykset.
2.3.1. Määrittele lausunto.
2.3.2. Listaa lausunnon päätoiminnot.
2.3.3. Mikä on totuustaulukko?
2.3.4. Luo totuustaulukot seuraaville kaavoille:
~ ~ ![]() ~ ;
~ ;
2.3.5. Ottaen huomioon operaatioiden järjestystä koskevat käytännöt, jätä kaavoista pois "ylimääräiset" sulkeet ja " "-merkki:
![]() ;
;
2.3.6. Todista kaavojen identtinen totuus käyttämällä ekvivalentteja muunnoksia:
2.3.7. Etsi kaksoiskaavat:
![]()
![]()
![]() )
)
2.3.8. Pienennä seuraavat kaavat täydelliseen DNF (SDNF) muotoon:
![]() ~
~
2.3.9. Pienennä seuraavat kaavat täydelliseen CNF (SCNF) muotoon:
![]()
![]() ~
~
![]()
![]()
Laboratoriotyö nro 3
Aihe:"Boolen funktioiden minimointi. Logiikka"
Kohde: Hankitaan käytännön taitoja työskennellä Boolen funktioiden minimointimenetelmien kanssa.
3.1. Teoreettista tietoa.
Minimaaliset muodot
Kuten näytettiin, mikä tahansa Boolen funktio voidaan esittää täydellisessä normaalimuodossa (disjunktiivi tai konjunktiivi). Lisäksi tällainen esitys on ensimmäinen askel siirtymisessä funktion taulukkomäärittelystä sen analyyttiseen ilmaisuun. Seuraavassa edetään disjunktiivimuodosta, ja vastaavat tulokset konjunktiivimuodolle saadaan kaksinaisuuden periaatteen perusteella.
Kanoninen ongelma loogisten piirien syntetisoinnissa Boolen pohjalta tiivistyy Boolen funktioiden minimoimiseen, ts. esittää ne disjunktiivisessa normaalimuodossa, joka sisältää pienimmän määrän kirjaimia (muuttujia ja niiden negatiivisia). Tällaisia muotoja kutsutaan minimaaliksi. Kanonisessa synteesissä oletetaan, että sekä signaalit että niiden inversiot syötetään piirin tuloihin.
Disjunktiivisessa normaalimuodossa esitettyä kaavaa yksinkertaistetaan käyttämällä toistuvasti liimausoperaatiota ja absorptiooperaatiota ja (konjunktiivisen normaalimuodon kaksoisidentiteetit ovat muotoa: ja ). Tässä ja voidaan ymmärtää minkä tahansa Boolen algebran kaavana. Tuloksena päästään analyyttiseen lausekkeeseen, jossa muut muunnokset eivät ole enää mahdollisia, ts. saamme umpikujamuodon.
Umpikujamuotojen joukossa on myös minimaalinen disjunktiivinen muoto, eikä se välttämättä ole ainutlaatuinen. Varmistaaksesi, että tietty umpikujalomake on minimaalinen, sinun on löydettävä kaikki umpikujalomakkeet ja verrattava niitä niiden sisältämien kirjainten lukumäärän mukaan.
Oletetaan esimerkiksi funktio täydellisessä normaalissa disjunktiivimuodossa:
Ryhmittelemällä termit ja soveltamalla liimausoperaatiota meillä on .
Toisella ryhmittelymenetelmällä saamme:
Molemmat umpikujamuodot eivät ole minimaalisia. Minimaalisen muodon saamiseksi sinun on arvattava toistaaksesi yksi termi alkuperäisessä kaavassa (tämän voi aina tehdä, koska ). Ensimmäisessä tapauksessa tällainen jäsen voi olla . Sitten . Lisäämällä termin , saamme: . Kun olet käynyt läpi kaikki mahdolliset vaihtoehdot, voit varmistaa, että kaksi viimeistä muotoa ovat minimaaliset.
Kaavojen kanssa työskentely tällä tasolla on kuin vaeltelua pimeässä. Minimaalisten muotojen etsintäprosessista tulee visuaalisempi ja tarkoituksenmukaisempi, jos käyttää joitain graafisia ja analyyttisiä esityksiä ja symboleita, jotka on erityisesti kehitetty tähän tarkoitukseen.
Moniulotteinen kuutio
Jokainen -ulotteisen kuution kärki voidaan liittää yksikön ainesosaan. Näin ollen merkittyjen pisteiden osajoukko on täydellisessä disjunktiivisessa normaalimuodossa olevien muuttujien Boolen funktion -ulotteisen kuution kartoitus. Kuvassa 3.1 esittää tällaisen funktion kuvauksen lausekkeesta 3.7.

Kuva 3.1 SDNF:ssä esitetyn funktion näyttö kolmiulotteisessa kuutiossa
Missä tahansa disjunktiivisessa normaalimuodossa esitettyjen muuttujien funktion näyttämiseksi on tarpeen luoda vastaavuus sen minitermien ja -ulotteisen kuution elementtien välille.
(-1) arvosanan minitermiä voidaan pitää tuloksena liimaamalla yhteen kaksi arvosanaa (yksinäisyyden ainesosa), ts. ![]() , -ulotteisessa kuutiossa tämä vastaa kahden sellaisen kärjen korvaamista, jotka eroavat vain koordinaatin arvoista, jotka yhdistävät nämä kärjet reunaan (reunan sanotaan peittävän siihen tulevat kärjet). Siten (-1):nnen kertaluvun minitermit vastaavat -ulotteisen kuution reunoja. Vastaavasti (-2) kertaluvun minitermien vastaavuus määritetään -ulotteisen kuution pintojen kanssa, joista jokainen peittää neljä kärkeä (ja neljä reunaa).
, -ulotteisessa kuutiossa tämä vastaa kahden sellaisen kärjen korvaamista, jotka eroavat vain koordinaatin arvoista, jotka yhdistävät nämä kärjet reunaan (reunan sanotaan peittävän siihen tulevat kärjet). Siten (-1):nnen kertaluvun minitermit vastaavat -ulotteisen kuution reunoja. Vastaavasti (-2) kertaluvun minitermien vastaavuus määritetään -ulotteisen kuution pintojen kanssa, joista jokainen peittää neljä kärkeä (ja neljä reunaa).
-ulotteisen kuution elementtejä, joille on tunnusomaista mitat, kutsutaan -kuutioiksi. Siten kärjet ovat 0-kuutiot, reunat 1-kuutiot, pinnat ovat 2-kuutiot jne. Yleistäen yllä olevaa päättelyä, voidaan olettaa, että ():nnen asteen minitermi disjunktiivisessa normaalimuodossa muuttujien funktiolle esitetään -kuutiolla, ja jokainen -kuutio kattaa kaikki ne pienemmän ulottuvuuden -kuutiot, jotka liittyvät sen kärkiin. . Esimerkkinä kuvassa. 3.2 esittää kolmen muuttujan funktiota. Tässä minitermit vastaavat 1-kuutiota (), ja minitermiä edustaa 2-kuutio ().

Kuva 3.2 Toiminnon kattavuus ![]()
Joten mikä tahansa disjunktiivinen normaalimuoto kartoitetaan -ulotteiseen kuutioon joukolla -kuutioita, jotka kattavat kaikki yksikön aineosia vastaavat kärjet (0-kuutiot). Myös käänteinen väite on totta: jos tietty joukko -kuutioita kattaa joukon kaikkia funktion yksikköarvoja vastaavia pisteitä, niin näitä -kuutioita vastaavien minitermien disjunktio on tämän funktion lauseke disjunktiivisessa normaalissa. muodossa. Tällaisen kokoelman -kuutioita (tai niitä vastaavia minitermejä) sanotaan muodostavan funktion peitteen.
Minimaalisen muodon halu ymmärretään intuitiivisesti sellaisen päällysteen etsimiseksi, jonka kuutioiden määrä olisi pienempi ja niiden mitat suurempi. Minimimuotoa vastaavaa kattavuutta kutsutaan minimikattavuudeksi. Esimerkiksi kuvan 1 peittotoiminnolle. 3.3 täyttää vähimmäislomakkeet ![]() Ja
Ja ![]() .
.

Riisi. 3.3 Toimintojen kattavuus.
vasemmalle – ![]() ; oikealla –
; oikealla – ![]()
 Toiminnon näyttäminen -ulotteisessa kuutiossa on selkeä ja yksinkertainen, kun . Neliulotteinen kuutio voidaan kuvata kuvan 1 mukaisesti. 3.4, joka näyttää neljän muuttujan funktion ja sen lauseketta vastaavan minimikattavuuden
Toiminnon näyttäminen -ulotteisessa kuutiossa on selkeä ja yksinkertainen, kun . Neliulotteinen kuutio voidaan kuvata kuvan 1 mukaisesti. 3.4, joka näyttää neljän muuttujan funktion ja sen lauseketta vastaavan minimikattavuuden ![]() . Tämän menetelmän käyttö vaatii niin monimutkaisia rakenteita, että kaikki sen edut menetetään.
. Tämän menetelmän käyttö vaatii niin monimutkaisia rakenteita, että kaikki sen edut menetetään.
Riisi. 3.4 Toimintojen näyttö ![]() neliulotteisessa kuutiossa
neliulotteisessa kuutiossa
Carnot kartat
Toinen menetelmä Boolen funktioiden graafiseen esittämiseen käyttää Carnot kartat, jotka ovat erityisesti järjestettyjä vastaavuustaulukoita. Taulukon sarakkeet ja rivit vastaavat kaikkia mahdollisia enintään kahden muuttujan arvojoukkoja, ja nämä joukot on järjestetty sellaiseen järjestykseen, että jokainen seuraava eroaa edellisestä vain yhden muuttujan arvossa. . Tämän ansiosta taulukon viereiset solut vaakasuunnassa ja pystysuunnassa eroavat vain yhden muuttujan arvosta. Taulukon reunoilla sijaitsevat solut katsotaan myös viereisiksi ja niillä on tämä ominaisuus. Kuvassa Kuva 3.5 näyttää Karnaugh-kartat kahdelle, kolmelle, neljälle muuttujalle.
 |
|||||
 |
|||||
 |
|||||
Riisi. 3.5 Carnaugh-kartat kahdelle, kolmelle ja neljälle muuttujalle
Kuten tavallisissa totuustaulukoissa, niiden joukkojen solut, joissa funktio saa arvon 1, täytetään ykkösillä (nollat eivät yleensä mahdu, ne vastaavat tyhjiä soluja). Esimerkiksi kuvassa Fig. 3.6, A esittää Karnaugh-kartan funktiolle, jonka näyttö neliulotteisessa kuutiossa on esitetty kuvassa 1. 3.4. Asioiden yksinkertaistamiseksi rivit ja sarakkeet, jotka vastaavat muuttujan arvoa 1, on korostettu tätä muuttujaa osoittavalla aaltosululla.
 |
|||
 |
|||
Riisi. 3.6 Neljän muuttujan funktion näyttäminen Carnaugh-kartalla
(a) ja sen vähimmäissuoja (b)
Funktiokartoitusten välillä n-ulotteinen kuutio ja Carnot-kartta ovat yksi-yhteen vastaavuus. Carnotin kartalla s-kuutio vastaa 2 vierekkäisen solun joukkoa, jotka on sijoitettu riviin, sarakkeeseen, neliöön tai suorakulmioon (ottaen huomioon kartan vastakkaisten reunojen läheisyyden). Siksi kaikki edellä mainitut määräykset (katso kohta. moniulotteinen kuutio), ovat voimassa Karnaugh-kartoissa. Joten kuvassa 3.6, b näyttää minimidisjunktiivimuotoa vastaavien karttayksiköiden kattavuuden ![]() kyseessä oleva toiminto.
kyseessä oleva toiminto.
Minitermien lukeminen Karnaugh-kartalta noudattaa yksinkertaista sääntöä. Solujen muodostuminen s-kuutio, anna miniter (n–s)-th rank, joka sisältää ne (n–s) muuttujat, jotka säilyttävät samat arvot tässä s-kuutio, jossa arvo 1 vastaa itse muuttujia ja arvo 0 vastaa niiden negaatioita. Muuttujat, jotka eivät säilytä arvojaan s-kuutio, ovat poissa minitermissä. Erilaiset lukutavat johtavat funktion erilaisiin esityksiin disjunktiivisessa normaalimuodossa (oikealla oleva minimaalinen) (kuva 3.7).
 |  |
||||||||
 |
|||||||||
Karnaugh-karttojen käyttö vaatii yksinkertaisempia rakenteita verrattuna kartoitukseen n-ulotteinen kuutio, erityisesti neljän muuttujan tapauksessa. Viiden muuttujan funktioiden näyttämiseksi käytetään kahta Karnaugh-karttaa neljälle muuttujalle ja kuuden muuttujan funktiolle neljää tällaista karttaa. Muuttujien määrän lisääntyessä Karnaugh-kartoista tulee käytännössä käyttökelvottomia.
Kuuluisa kirjallisuudessa Veitch-kortit Ne eroavat vain muuttujaarvojoukkojen eri järjestyksessä ja niillä on samat ominaisuudet kuin Karnaugh-kartoilla.
Kuutioiden kompleksi
Graafisten menetelmien epäjohdonmukaisuus suurella määrällä muuttujia kompensoidaan erilaisilla analyyttisilla menetelmillä Boolen funktioiden esittämiseksi. Yksi tällainen esitys on kuutioiden kompleksi, jossa käytetään moniulotteisen loogisen tilan terminologiaa yhdistettynä erityisesti kehitetyn symboliikkaan.
). 0-kuutiot, jotka vastaavat yhtenäisyyden ainesosia, esitetään muuttuja-arvojoukoilla, joilla funktio on yhtä suuri kuin yksikkö. Ilmeisesti äänityksessä


Riisi. 3.8 Kolmen muuttujan funktion kuutioiden kompleksi ( A) ja sen symbolinen esitys ( b)
Kuutioiden kompleksi muodostuu maksimaalinen toimintopeitto. Sulkemalla pois kaikki nuo s-kuutiot, jotka on peitetty korkeamman ulottuvuuden kuutioilla, saadaan umpikujamuotoja vastaavat päällysteet. Tarkasteltavalle esimerkille (kuva 3.8) on siis umpikuja
 ,
,
joka vastaa toimintoa ![]() . Tässä tapauksessa tämä kattavuus on minimaalinen.
. Tässä tapauksessa tämä kattavuus on minimaalinen.
Kahden Boolen funktion disjunktiooperaatio vastaa niiden kuutiokompleksien liittoa ja konjunktiooperaatio vastaa niiden kuutiokompleksien leikkauskohtaa. Funktion negaatio vastaa kuutiokompleksin komplementtia, eli sen määräävät kaikki kärjet, joissa funktio saa arvon 0. Siten funktion algebran välillä on yksi yhteen vastaavuus (isomorfismi). Boolen funktiot ja Boolen joukot, jotka edustavat kuutioiden komplekseja.
Funktion esittäminen kuutiokompleksien muodossa on vähemmän visuaalista, mutta sen tärkeimmät edut ovat muuttujien lukumäärän rajoitusten poistaminen ja tiedon koodaus helpottuu tietokoneita käytettäessä.
Boolen funktioiden minimoiminen
Ongelman muotoilu. Piirin minimointi Boolen perusteella tarkoittaa, että löydetään vähimmäiskattavuutta vastaava vähimmäisdisjunktiivimuoto. Normaalimuodossa olevien kirjeiden kokonaismäärä ilmaistaan peittokuluina ![]() , missä on niiden kuutioiden lukumäärä, jotka muodostavat tietyn n muuttujan funktion peitteen. Minimikattavuudelle on ominaista sen hinnan alhaisin arvo.
, missä on niiden kuutioiden lukumäärä, jotka muodostavat tietyn n muuttujan funktion peitteen. Minimikattavuudelle on ominaista sen hinnan alhaisin arvo.
Tyypillisesti minimointiongelma ratkaistaan kahdessa vaiheessa. Ensin etsimme pienennettyä kantta, joka sisältää kaikki maksimimittaiset -kuutiot, mutta ei sisällä ainuttakaan kuutiota, jonka yksikään tämän kannen kuutio peittää. Vastaavaa disjunktiivista normaalimuotoa kutsutaan pelkistetyksi ja sen minitermejä yksinkertaisiksi implikantteiksi. Tietylle toiminnolle alennettu peitto on ainutlaatuinen, mutta se voi olla tarpeeton, koska osa kuutioista on muiden kuutioiden kokoelman peitossa.
Toisessa vaiheessa siirrytään pelkistetyistä disjunktiivisista normaalimuodoista umpikujaan, joista valitaan minimaaliset muodot. Umpikujamuodot muodostetaan jättämällä pois supistetusta kattavuudesta kaikki ylimääräiset kuutiot, joita ilman jäljellä oleva kuutiojoukko muodostaa edelleen tietyn funktion peitteen, mutta jos jokin kuutioista edelleen jätetään pois, se ei enää kata kaikkien kuutioiden joukkoa. funktion yksittäisiä arvoja vastaavat kärjet, eli se lakkaa olemasta peitto .
Pienennetty peittokuutio, joka kattaa tietyn funktion kärjet, joita muut kuutiot eivät peitä, ei voi olla redundantti, ja se sisällytetään aina vähimmäispeittoon. Tällaista kuutiota, kuten sen vastaavaa implikanttia, kutsutaan äärimmäiseksi (olennainen implikantti), ja sen peittämiä kärkipisteitä kutsutaan peruutetuiksi pisteiksi. Extremaalien joukko muodostaa päällysteen ytimen, on selvää, että siirryttäessä supistetusta kattavuudesta minimaaliseen tulee ensinnäkin eristää kaikki ääripäät. Jos ääripääjoukko ei muodosta peitettä, sitä täydennetään peittämällä kuutioilla pelkistetystä päällysteestä.
Annetut määritelmät on havainnollistettu kuvassa. 3.9, jossa kattavuus on pienempi (katso kuva 3.9a, ) ja vähimmäispeitot (kuva 3.9b) ja (katso kuva 3.9, b) ilmaistaan seuraavasti.