Loogisen funktion konjunktiivinen normaalimuoto. Boolen funktioiden erikoisesitykset. Esimerkkejä sknf:stä joillekin toiminnoille
Määritelmä 1.Konjunktiivinen monomiaali (alkeiskonjunktio) muuttujien konjunktio on näiden muuttujien tai niiden negaatioiden konjunktio.
Esimerkiksi, on alkeiskonjunktio.
Määritelmä 2.Disjunktiivinen monomiaali (alkeisdisjunktio) muuttujista on näiden muuttujien disjunktio tai niiden negaatiot.
Esimerkiksi, on alkeisdisjunktio.
Määritelmä 3. Kaava, joka vastaa annettua lausealgebran kaavaa ja on alkeiskonjunktiivisten monomien disjunktio, kutsutaan disjunktiivinen normaalimuoto(DNF) tämän kaavan mukaisesti.
Esimerkiksi,– DNF.
Määritelmä 4. Kaava, joka vastaa annettua lausealgebran kaavaa ja on alkeisdisjunktiivisten monomien konjunktio, kutsutaan konjunktiivinen normaalimuoto(CNF) tämän kaavan mukaisesti.
Esimerkiksi, – KNF.
Jokaiselle lausealgebran kaavalle voidaan löytää joukko disjunktiivisia ja konjunktiivisia normaalimuotoja.
Algoritmi normaalimuotojen muodostamiseksi
Käytä loogisen algebran ekvivalensseja, korvaa kaikki kaavan perustoiminnot: konjunktio, disjunktio, negaatio:
Päästä eroon kaksoisnegatiivista.
Käytä tarvittaessa distributiivisuus- ja absorptiokaavojen ominaisuuksia konjunktio- ja disjunktiooperaatioihin.
2.6. Täydelliset disjunktiiviset ja täydelliset konjunktiiviset normaalimuodot
Jokaisella Boolen funktiolla voi olla useita esityksiä DNF- ja CNF-muodossa. Erityinen paikka näiden esitysten joukossa on täydellinen DNF (SDNF) ja täydellinen CNF (SCNF).
Määritelmä 1. Täydellinen disjunktiivinen normaalimuoto(SDNF) on DNF, jossa jokainen konjunktiivinen monomi sisältää jokaisen muuttujan joukosta täsmälleen kerran, joko itsensä tai sen negatiivisen.
Rakenteellisesti kunkin lausealgebrakaavan SDNF, joka on pelkistetty DNF:ksi, voidaan määritellä seuraavasti:
Määritelmä 2. Täydellinen disjunktiivinen normaalimuoto Propositioalgebrakaavan (SDNF) kutsutaan sen DNF:ksi, jolla on seuraavat ominaisuudet:
Määritelmä 3. Täydellinen konjunktiivinen normaalimuoto(SCNF) on CNF, jossa jokainen disjunktiivinen monomi sisältää jokaisen muuttujan joukosta täsmälleen kerran, ja joko itse tai sen negaatio ilmestyy.
Rakenteellisesti kunkin lausealgebrakaavan SCNF, joka on pelkistetty CNF:ksi, voidaan määritellä seuraavasti.
Määritelmä 4. Täydellinen konjunktiivinen normaalimuoto Tietyn lausealgebrakaavan (SCNF) kutsutaan CNF:ksi, joka täyttää seuraavat ominaisuudet.
Lause 1. Jokainen muuttujien Boolen funktio, joka ei ole identtisesti epätosi, voidaan esittää SDNF:ssä ja ainutlaatuisella tavalla.
Menetelmät SDNF:n löytämiseksi
1. menetelmä
2. menetelmä
valitse rivit, joissa kaava saa arvon 1;
muodostamme konjunktioiden disjunktion sillä ehdolla, että jos muuttuja sisältyy konjunktioon, jonka arvo on 1, niin tämä muuttuja kirjoitetaan muistiin; jos arvolla 0, niin sen negaatio. Saamme SDNF:n.
Lause 2. Jokainen muuttujien Boolen funktio, joka ei ole identtisesti tosi, voidaan esittää SCNF:ssä ja ainutlaatuisella tavalla.
Menetelmät SCNF:n löytämiseksi
1. menetelmä– käyttämällä vastaavia muunnoksia:
2. menetelmä– käyttämällä totuustaulukoita:
valitse rivit, joissa kaava saa arvon 0;
muodostamme disjunktioiden konjunktion sillä ehdolla, että jos disjunktioon sisältyy muuttuja, jonka arvo on 0, niin tämä muuttuja kirjoitetaan muistiin, jos arvolla 1, niin sen negaatio. Saamme SKNF:n.
Esimerkki 1. Muodosta CNF-funktiot.
Ratkaisu
Poistetaan yhdistävä "" käyttämällä muuttujien muunnoslakeja:
= /de Morganin lait ja kaksoisnegatio/ =
/jakelulait/ =
Esimerkki 2. Anna kaava DNF:lle.
Ratkaisu
Ilmaistaan loogiset toiminnot käyttämällä ja:
= /luokitetaan negaatio muuttujiksi ja vähennetään kaksinkertaiset negatiivit/ =
= /jakauman laki/ .
Esimerkki 3. Kirjoita kaava muodossa DNF ja SDNF.
Ratkaisu
Käytämme logiikan lakeja, pelkistämme tämän kaavan muotoon, joka sisältää vain alkeiskonjunktioiden disjunktiot. Tuloksena oleva kaava on haluttu DNF:
SDNF:n muodostamiseksi luodaan totuustaulukko tälle kaavalle:
Merkitsemme ne taulukon rivit, joissa kaava (viimeinen sarake) saa arvon 1. Jokaiselle tällaiselle riville kirjoitetaan kaava, joka on tosi tämän rivin muuttujien joukkoon:
rivi 1: ;
rivi 3: ;
rivi 5: .
Näiden kolmen kaavan disjunktio saa arvon 1 vain rivien 1, 3, 5 muuttujajoukoissa ja on siksi haluttu täydellinen disjunktiivinen normaalimuoto (PDNF):
Esimerkki 4. Tuo kaava SKNF:lle kahdella tavalla:
a) käyttämällä vastaavia muunnoksia;
b) käyttämällä totuustaulukkoa.
Ratkaisu:
Muunnetaan toinen alkeisdisjunktio:
Kaava näyttää tältä:
b) laadi totuustaulukko tälle kaavalle:
Merkitsemme ne taulukon rivit, joissa kaava (viimeinen sarake) saa arvon 0. Jokaiselle tällaiselle riville kirjoitetaan kaava, joka on tosi tämän rivin muuttujien joukkoon:
linja 2: ;
rivi 6: .
Näiden kahden kaavan konjunktio saa arvon 0 vain rivien 2 ja 6 muuttujajoukoissa ja on siksi haluttu täydellinen konjunktiivinen normaalimuoto (PCNF):
Kysymyksiä ja tehtäviä itsenäiseen ratkaisuun
1. Käytä vastaavia muunnoksia, vähennä kaavat DNF:ksi:
2. Käytä vastaavia muunnoksia, tuo kaavat CNF:ään:
3. Muunna DNF CNF:ksi käyttämällä toista distributiivista lakia:
A) ![]() ;
;
4. Muunna annetut DNF:t SDNF:iksi:
5. Muunna annettu CNF SCNF:ksi:
6. Muodosta SDNF ja SCNF annetuille loogisille kaavoille kahdella tavalla: käyttämällä vastaavia muunnoksia ja käyttämällä totuustaulukkoa.
b) ![]() ;
;
Yksinkertainen disjunktio(eng. inclusive disjunktion) tai disjunktio(englanniksi disjunct) on yhden tai useamman muuttujan tai niiden negaatioiden disjunktio, jossa jokainen muuttuja esiintyy enintään kerran.
Yksinkertainen disjunktio
- koko, jos jokainen muuttuja (tai sen negaatio) esiintyy täsmälleen kerran;
- yksitoikkoinen, jos se ei sisällä muuttujien negaatioita.
Konjunktiivinen normaalimuoto, CNF(eng. konjunktiivinen normaalimuoto, CNF) normaalimuoto, jossa Boolen funktiolla on useiden yksinkertaisten lauseiden konjunktio.
CNF esimerkki:$f(x,y) = (x \lor y) \land (y \lor \neg ( z ))$
SKNF
Täydellinen konjunktiivinen normaalimuoto, SCNF(englanniksi täydellinen konjunktiivinen normaalimuoto, PCNF) on CNF, joka täyttää ehdot:
- se ei sisällä identtisiä yksinkertaisia disjunktioita
- jokainen yksinkertainen disjunktio on valmis
SKNF esimerkki:$f(x,y,z) = (x \lor \neg ( y ) \lor z) \land (x\lor y \lor \neg ( z ))$
Lause: Jokaiselle Boolen funktiolle $f(\vec ( x ))$, joka ei ole sama kuin identiteetti, on olemassa SCNF, joka määrittää sen.
Todiste: Koska funktion $\neg ( f ) (\vec x)$ käänteisarvo on yhtä suuri kuin yksi niissä joukoissa, joissa $f(\vec x)$ on nolla, niin $\neg ( f ) SDNF (\vec x)$ voidaan kirjoittaa seuraavasti:
$\neg ( f ) (\vec x) = \bigvee\limits_ ( f(x^ ( \sigma_ ( 1 ) ) , x^ ( \sigma_ ( 2 ) ), ... ,x^ ( \sigma_ ( n ) ) )) = 0 ) (x_ ( 1 ) ^ ( \sigma_ ( 1 ) ) \wedge x_ ( 2 ) ^ ( \sigma_ ( 2 ) ) \wedge ... \wedge x_ ( n ) ^ ( \sigma_ ( n ) ) )) $, jossa $ \sigma_ ( i ) $ tarkoittaa negatiivisen olemassaoloa tai puuttumista kohdassa $ x_ ( i ) $
Etsitään lausekkeen vasemman ja oikean puolen käännös:
$ f(\vec x) = \neg (( \bigvee\limits_ ( f(x^ ( \sigma_ ( 1 ) ) ), x^ ( \sigma_ ( 2 ) ), ... ,x^ ( \sigma_ ( n ) )) = 0 ) (x_ ( 1 ) ^ ( \sigma_ ( 1 ) ) \wedge x_ ( 2 ) ^ ( \sigma_ ( 2 ) ) \wedge ... \wedge x_ ( n ) ^ ( \sigma_ ( n ) ) )) )) $
Kun de Morganin sääntöä sovelletaan kahdesti oikealla puolella saatuun lausekkeeseen, saadaan: $ f(\vec x) = \bigwedge \limits_ ( f(x^ ( \sigma_1 ) , x^ ( \sigma_2 ) , \dots ,x ^ ( \ sigma_n )) = 0 ) $ $(\neg ( x_1^ ( \sigma_1 ) ) \vee \neg ( x_2^ ( \sigma_2 ) ) \vee \dots \vee \neg ( x_n^ ( \sigma_n ) ) ) $
Viimeinen lauseke on SKNF. Koska SCNF saadaan SDNF:stä, joka voidaan konstruoida mille tahansa funktiolle, joka ei ole identtinen nolla, lause on todistettu.
Algoritmi SCNF:n muodostamiseksi totuustaulukon avulla
- Totuustaulukkoon merkitään ne muuttujajoukot, joille funktion arvo on $0$.
- Jokaiselle merkitylle joukolle kirjoitetaan kaikkien muuttujien disjunktio seuraavan säännön mukaan: jos jonkin muuttujan arvo on $0$, sisällytetään disjunktioon itse muuttuja, muuten sen negaatio.
- Yhdistämme kaikki tuloksena olevat disjunktiot konjunktiooperaatioilla.
Esimerkki SCNF:n rakentamisesta mediaanille
1). Totuustaulukkoon merkitään ne muuttujajoukot, joille funktion arvo on $0$.
| x | y | z | $ \langle x,y,z \rangle $ |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
2). Jokaiselle merkitylle joukolle kirjoitetaan kaikkien muuttujien konjunktio seuraavan säännön mukaan: jos jonkin muuttujan arvo on $0$, sisällytetään disjunktioon itse muuttuja, muuten sen negaatio.
| x | y | z | $ \langle x,y,z \rangle $ | |
| 0 | 0 | 0 | 0 | $(x \lor y \lor z)$ |
| 0 | 0 | 1 | 0 | $(x \lor y \lor \neg ( z ))$ |
| 0 | 1 | 0 | 0 | $(x \tai \neg ( y ) \tai z)$ |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | $(\neg ( x ) \tai y \tai z)$ |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 |
3). Yhdistämme kaikki tuloksena olevat disjunktiot konjunktiooperaatioilla.
$ \langle x,y,z \rangle = (x \lor y \lor z) \land (\neg ( x ) \lor y \lor z) \land (x \lor \neg ( y ) \lor z) \maa (x \lor y \lor \neg ( z ))$
Esimerkkejä SKNF:stä joillekin toiminnoille
Peircen nuoli: $ x \downarrow y = (\neg ( x ) \lor ( y )) \land (( x ) \lor \neg ( y )) \land (\neg ( x ) \lor \neg ( y ) ) $
Yksinomainen tai: $ x \oplus y \oplus z = (\neg ( x ) \lor \neg ( y ) \lor z) \land (\neg ( x ) \lor y \lor \neg ( z )) \maa (x \lor \neg ( y ) \lor \neg ( z )) \land (x \lor y \lor z)$
Vakioperuste. Elementaariset kaavat ovat literaaleja. Elementaarinen konjunktio (disjunktio). Disjunktiivinen (konjunktiivinen) normaalimuoto ja täydellinen muoto. Lause: mikä tahansa Boolen funktio, joka poikkeaa 0:sta (1:stä), voidaan esittää SDNF:n (SCNF) muodossa. Vakiopohjan täydellisyys. Esimerkkejä täydellisistä emäksistä: Zhegalkin-pohja, Schaeffer-viiva, Peirce-nuoli.
Vakioperuste on joukko Boolen algebran kolmea perusoperaatiota: yhteenlasku (liitos), kertolasku (leikkaus) ja negaatio.
Täällä soitetaan kirjaimellinen muuttuja x tai sen negaatio x ja merkitsee xˆ. Boolen leikkauspiste useista eri muuttujilla määritellyistä literaaleista, ts. muodon X = xˆ 1 xˆ 2 lauseke. . . xˆ l, soitettu alkeisyhdistys . Vaatimus, että kaikki muuttujat ovat erilaisia, määräytyy seuraavalla. Jos konjunktiossa on useita identtisiä literaaleja, niin konjunktion kommutatiivisuudesta, assosiatiivisuudesta ja idempotenssista johtuen on mahdollista ekvivalenttiin kaavaan siirtyessä jättää vain yksi literaali (esim. x 1 x 1 = x 1). Jos konjunktiossa on muuttuja ja sen negaatio, niin kaava on ekvivalentti vakion 0 kanssa, koska x x = 0 ja mille tahansa kaavalle Y meillä on Y x x = 0.
Useiden alkeiskonjunktioiden disjunktiota kutsutaan disjunktiivinen normaalimuoto , tai DNF . Esimerkiksi,
x 1 x 3 + x 2 x 3 x 4 + x 1 x 2 x 3 x 5 .
Jos muuttujien koostumus tietyn DNF:n jokaisessa alkeiskonjunktiossa on sama, niin DNF on ns. täydellinen . Annettu esimerkki on DNF, joka ei ole täydellinen. Päinvastoin, kaava
x 1 x 2 x 3 x 4 + x 1 x 2 x 3 x 4 + x 1 x 2 x 3 x 4
on täydellinen muoto.
Koska Boolen algebrassa yhteen- ja kertolasku ovat symmetrisiä operaatioita ja yhteenlasku voidaan aina tulkita kertolaskuksi ja kertolasku yhteenlaskuksi, on olemassa kaksoiskäsite - konjunktiivinen normaalimuoto (KNF ), joka on alkeisdisjunktioiden konjunktio ja täydellinen konjunktiivimuoto (SKNF ). Symmetristen puolijohteiden duaalisuuden periaatteesta seuraa, että kaikkiin DNF:ää koskeviin väitteisiin vastataan kaksoislauseella CNF:stä, joka saadaan korvaamalla yhteenlasku (disjunktio) kertolaskulla, kertolasku (konjunktio) yhteenlaskulla, vakio 0 vakiolla 1, vakio. 1 vakiolla 0, järjestyssuhde duaaliin (käänteinen) järjestyksessä. Siksi keskitymme edelleen vain DNF:n tutkimiseen.
Lause 1.4. Mikä tahansa muu Boolen funktio kuin vakio 0 voidaan esittää SDNF:nä.
◀Sopikaa, että x σ:llä tarkoitamme kaavaa x, jos σ = 1, ja kaavaa x, jos σ = 0. Olkoon funktio f(y 1 , . . . , y n) arvo 1 vektorissa (t) 1 , ... , t n ) (tällaista vektoria kutsutaan osatekijä ). Silloin alkeiskonjunktio saa myös arvon 1 tässä joukossa, mutta katoaa kaikista muista n-ulotteisista Boolen vektoreista. Harkitse kaavaa
jossa summa (liitto) ulottuu kaikkiin argumenttiarvojen joukkoihin (t 1, . . . , t n), joille annettu funktio saa arvon 1. Huomaa, että tällaisten joukkojen joukko ei ole tyhjä, joten summa sisältää vähintään yhden termin.
On helppo nähdä, että kaavasta Φ tulee 1 niille ja vain niille muuttujien arvoille, joille kyseessä olevasta funktiosta tulee 1. Tämä tarkoittaa, että kaava Ψ edustaa funktiota f.
Seuraus 1.1. Vakiopohja on valmis.
◀ Itse asiassa, jos funktio ei ole vakio 0, se voidaan esittää joko SDNF:n muodossa, joka on kaava vakioperusteen yli. Vakio 0 voidaan esittää esimerkiksi kaavalla f(x 1, x 2, . . . , x n) = x 1 x 1.
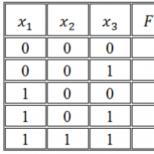
Esimerkki 1.2. Tarkastellaan kolmen muuttujan funktiota m(x 1, x 2, x 3) (taulukko 1.4), ns. enemmistötehtävä ̆. Tämän funktion arvo on 1, jos yli puolella sen argumenteista on arvo 1. Siksi sitä kutsutaan usein äänestysfunktioksi. Rakennetaan sille SDNF.
Vakiopohjan täydellisyys mahdollistaa muiden täydellisten toimintojärjestelmien valitsemisen. Joukon F täydellisyys voidaan määrittää seuraavista näkökohdista. Oletetaan, että jokainen kolmesta vakioväyläfunktiosta on esitettävissä kaavalla F :n päällä. Sitten Lauseen 1.3 mukaan identiteetti F on täydellinen.
Esimerkki 1.3. Kutsutaan operaatioiden joukko modulo 2 yhteen-, kertolasku- ja vakio 1 Zhegalkinin perusteella . Yhteenlaskumoduuli 2 ja kertolasku ovat Z2-renkaan perusoperaatioita, niiden avulla muodostetut lausekkeet ovat Z2-renkaan yli olevia polynomeja. Vakio 1 on tässä tapauksessa välttämätön vapaan termin kirjoittamiseen. Koska xx = x, niin kaikilla polynomin tekijöillä on aste 1. Siksi polynomia kirjoitettaessa voit tehdä ilman asteen käsitettä. Esimerkkejä Zhegalkin-pohjaisista kaavoista:
xy⊕x⊕y, x⊕1, xyz⊕xz⊕x⊕y⊕1.
Mitä tahansa tällaista kaavaa kutsutaan Zhegalkin-polynomiksi. Itse asiassa Zhegalkin-polynomi on polynomi renkaan Z2 yli.
Ei ole vaikeaa rakentaa Zhegalkin-kannan päälle kaavoja, jotka edustavat vakiokannan yhteen- ja negatiivisuusoperaatioita (kahden kannan kertominen on yleistä):
x+y=x⊕y⊕xy, x =x⊕1.
Siksi Zhegalkin-pohja on täydellinen sarja.
Voidaan osoittaa, että mille tahansa Boolen funktiolle Zhegalkin-polynomi on yksilöllisesti määritelty
(tarkemmin sanottuna ehtojen järjestykseen asti). Zhegalkin-polynomin kertoimet pienellä määrällä muuttujia voidaan löytää määrittelemättömien kertoimien menetelmällä.
Esimerkki 1.4. Tarkastellaan yksittäisen funktion joukkoa - Schaeffer-iskua*. Tämä sarja on valmis seuraavien helposti todennettavien henkilöllisyyksien perusteella:
x =x|x, xy=x|y =(x|y)|(x|y), x+y=x |y =(x|x)|(y|y).
Esimerkki 1.5. Myös yhdestä funktiosta, Peircen nuolesta, koostuva kanta on valmis. Tämän testi on samanlainen kuin Schaefferin aivohalvauksen tapauksessa. Tämä johtopäätös voidaan kuitenkin tehdä myös symmetristen puolirenkaiden kaksinaisuuden periaatteen perusteella.
*Schaefferin veto on binäärinen, mutta ei assosiatiivinen operaatio. Siksi, kun käytät infix-lomaketta, sinun tulee olla varovainen: tulos riippuu toimintojen järjestyksestä. Tässä tapauksessa on suositeltavaa ilmoittaa operaatioiden järjestys suluilla, esimerkiksi kirjoittaa (x | y) | z, ei x | y | z, vaikka molemmat muodot ovat samanarvoisia.
Loogisten funktioiden normaalimuodot Boolen funktion esitystä yksikön Ki 2.7 aineosien konjunktiivitermien disjunktiomuodossa kutsutaan tämän funktion DNF:n disjunktiiviseksi normaalimuodoksi. sisältää täsmälleen yhden kaikista loogisista muuttujista negaatioilla tai ilman, niin tätä funktion esitysmuotoa kutsutaan tämän funktion täydelliseksi disjunktiiviseksi normaalimuodoksi SDNF. Kuten näet, kun kirjoitat SDNF-funktiota, sinun on luotava disjunktio kaikista mintermeistä, joille funktio saa arvon 1.
Jaa työsi sosiaalisessa mediassa
Jos tämä työ ei sovi sinulle, sivun alalaidassa on luettelo vastaavista teoksista. Voit myös käyttää hakupainiketta
Luento 1.xx
Loogisten funktioiden normaalit muodot
Boolen funktion esitys konjunktiivitermien disjunktiona (yksikön ainesosa) K i
, (2.7)
nimeltään disjunktiivinen normaalimuoto(DNF) tämän toiminnon.
Jos kaikki DNF:n konjunktiivitermit ovat minterms , eli ne sisältävät täsmälleen yhden kaikista loogisista muuttujista negatiivisten kanssa tai ilman, niin tätä funktion esitysmuotoa kutsutaantäydellinen disjunktiivinen normaalimuoto(SDNF ) tämä toiminto. Sitä kutsutaan SDNF:ksi täydellinen , koska jokainen disjunktion termi sisältää kaikki muuttujat; disjunktiivinen , koska kaavan pääoperaatio on disjunktio. Konsepti "normaali muoto” tarkoittaa yksiselitteistä tapaa kirjoittaa kaava, joka toteuttaa tietyn funktion.
Yllä oleva huomioon ottaen Lauseesta 2.1 seuraa seuraava lause.
Lause 2. Mikä tahansa Boolen funktio(ei identtisesti 0) voidaan esittää SDNF:ssä, .
Esimerkki 3. Otetaan taulukkoon annettu funktio f (x 1 , x 2 , x 3 ) (taulukko 10).
Taulukko 10
|
f (x 1 , x 2 , x 3 ) |
|||
Kaavan (2.6) perusteella saamme:
Kuten näet, kun kirjoitat SDNF-funktiota, sinun on luotava disjunktio kaikista mintermeistä, joille funktio saa arvon 1.
Boolen funktion esitys disjunktiivisten termien konjunktiona (nolla aineosa) D i
, (2.8)
nimeltään konjunktiivinen normaalimuoto(CNF) tämän toiminnon.
Jos kaikki disjunktiiviset CNF-termit ovat maxterms , eli ne sisältävät täsmälleen yhden funktion kaikista loogisista muuttujista negaatioiden kanssa tai ilman, silloin tällaista CNF:ää kutsutaantäydellinen konjunktiivinen normaalimuoto(SKNF) tämän toiminnon.
Lause 3. Mikä tahansa Boolen funktio(ei ole identtinen 1:n kanssa) voidaan toimittaa SKNF:lle, ja tällainen esitys on ainoa.
Lauseen todistus voidaan suorittaa samalla tavalla kuin Lauseen 2.1 todistus perustuen seuraavaan konjunktiivisen hajonnan Shannonin lemmaan.
Shannonin Lemma . Mikä tahansa Boolen funktio f (x 1, x 2, …, x m) m:stä muuttujat voidaan esittää näin:
. (2.9)
On huomattava, että molemmat loogisen funktion esitysmuodot (DNF ja CNF) ovat teoreettisesti samanlaisia ominaisuuksiltaan: mikä tahansa looginen kaava voidaan esittää sekä DNF:ssä (paitsi identtinen nolla) että CNF:ssä (paitsi identtinen). ). Tilanteesta riippuen funktion esitys muodossa tai toisessa voi olla lyhyempi.
Käytännössä käytetään useimmiten DNF:ää, koska tämä muoto on henkilölle tutumpi: lapsuudesta lähtien hän on tottunut lisäämään tuloja kuin kertomaan summia (jälkimmäisessä tapauksessa hänellä on intuitiivisesti halu avata sulut ja siirtyä siten DNF:ään).
Esimerkki 4. Funktiolle f (x 1 , x 2 , x 3 ), taulukon mukaan. 10, kirjoita se SKNF:lle.
Toisin kuin SDNF, kun käännät SCNF:ää loogisen funktion totuustaulukkoon, sinun on tarkasteltava muuttujien yhdistelmiä, joissa funktio saa arvon 0, ja luotava konjunktio vastaavista max termeistä,mutta muuttujat on otettava käänteisellä inversiolla:
On huomattava, että on mahdotonta siirtyä suoraan funktion SDNF:stä sen SCNF:ään tai päinvastoin. Kun tällaisia muunnoksia yritetään, tulokset ovat funktioita, jotka ovat päinvastaisia kuin halutut. SDNF- ja SCNF-funktioiden lausekkeet voidaan saada suoraan vain sen totuustaulukosta.
Esimerkki 5. Funktiolle f (x 1 , x 2 , x 3 ), taulukon mukaan. 10, yritä vaihtaa SDNF:stä SKNF:ään.
Käyttämällä esimerkin 2.3 tulosta saadaan:
Kuten näet, yleisen käännöksen alla saimme loogisen funktion SCNF:n, joka on käänteisarvo esimerkissä 2.4 saadulle funktiolle:
koska se sisältää kaikki maksimitermit, jotka eivät ole tarkasteltavana olevan funktion SCNF:n lausekkeessa.
1. Käyttämällä operaatioiden ominaisuuksia (katso taulukko 9) identiteetti (), sum modulo 2 (), implikaatio (), siirrymme operaatioihin AND, OR, NOT (Boolen perusteella).
2. Negaation ominaisuuksia ja De Morganin lakeja käyttämällä (katso taulukko 9) varmistamme, että negatiiviset operaatiot koskevat vain yksittäisiä muuttujia, eivät kokonaisia lausekkeita.
3. Käyttäen loogisten operaatioiden JA ja TAI ominaisuuksia (katso Taulukko 9) saadaan normaalimuoto (DNF tai CNF).
4. Siirry tarvittaessa täydellisiin muotoihin (SDNF tai SKNF). Esimerkiksi saadaksesi SCNF:n sinun on usein käytettävä ominaisuutta: .
Esimerkki 6. Muunna looginen funktio SKNF:ksi
Suorittamalla yllä olevan algoritmin vaiheet järjestyksessä, saamme:
Absorptio-ominaisuutta käyttämällä saamme:
Siten olemme saaneet CNF-funktion f (x 1 , x 2 , x 3 ). Saadaksesi sen SCNF, sinun on toistettava jokainen disjunktio, josta jokin muuttuja puuttuu, kahdesti tällä muuttujalla ja sen negaatiolla:
2.2.6. Loogisten funktioiden minimoiminen
Koska sama looginen funktio voidaan esittää h henkilökohtaisia kaavoja ja löytää sitten yksinkertaisin muoto R muuli, joka määrittelee Boolen funktion, yksinkertaistaa logiikkapiiriä, joka toteuttaa Boolen funktion tiota. Vähimmäismuoto l O looginen toimintojollain perusteella voimme pitää sellaista, joka sisältää minimimäärän hauskoja superpositioita Vastaanottaja perusteen mukaan sulkeet sallien. Tehokasta on kuitenkin vaikea rakentaa l algoritmi tällaiselle minimointille minimisulkujen saamiseksi r me.
Tarkastellaan yksinkertaisempaa minimointiongelmaa yhdistelmäpiirien synteesissä, jossa ei etsitä funktion minimaalista sulkumuotoa, vaan sen minimaalista DNF:ää. Tähän tehtävään on olemassa yksinkertaisia, tehokkaita algoritmeja.
Quinen menetelmä
Minimoitava funktio esitetään SDNF:ssä ja siihen sovelletaan kaikki mahdolliset epätäydelliset liimaustoimenpiteet
, (2.10)
ja sitten imeytyminen
, (2.11)
ja tätä vaiheparia sovelletaan toistuvasti. Siten on mahdollista alentaa termien järjestystä. Tätä menettelyä toistetaan, kunnes jäljellä ei ole yhtään termiä, joka voidaan liittää mihinkään muuhun termiin.
Huomaa, että yhtälön (2.10) vasen puoli voidaan minimoida välittömästi yksinkertaisemmalla ja selkeämmällä tavalla:
Tämä menetelmä on huono, koska tällaisella suoralla minimoitumisella konjunktiivitermit joko häviävät, vaikka on vielä mahdollisia tapauksia, joissa niitä käytetään liimaamiseen ja absorptioon muiden termien kanssa.
On huomattava, että Quinen menetelmä on melko työvoimavaltainen, joten virheiden todennäköisyys muutosten aikana on melko korkea. Mutta sen etuna on, että teoriassa sitä voidaan käyttää mihin tahansa argumenttien määrään ja muuttujien määrän kasvaessa muunnokset yksinkertaistuvat.
Karnaughin karttamenetelmä
Carnot-karttojen (taulukoiden) menetelmä on visuaalisempi, vähemmän työvoimavaltainen ja luotettava tapa minimoida loogisia funktioita, mutta sen käyttö rajoittuu käytännössä 3-4 muuttujan funktioihin, maksimi 5-6 muuttujaan.
Carnot kartta Tämä on kaksiulotteinen taulukkomuoto, joka esittää Boolen funktion totuustaulukon, jonka avulla voit helposti löytää loogisten funktioiden vähimmäis-DNF:t graafisessa visuaalisessa muodossa. Jokainen taulukon solu liittyy minimoitavan funktion SDNF-mintermiin ja siten, että taulukon mitkä tahansa symmetria-akselit vastaavat vyöhykkeitä, jotka ovat keskenään käänteisiä jonkin muuttujan suhteen. Tämä solujen järjestely taulukossa helpottaa SDNF:n tarttumistermien määrittämistä (poikkeavat vain yhden muuttujan inversiomerkistä): ne sijaitsevat taulukossa symmetrisesti.
Totuustaulukot ja Carnaugh-kartat kahden kaistan JA- ja TAI-funktioille e Muuttujat on esitetty kuvassa. 8. Kortin jokaiseen soluun kirjoitetaan arvo A Tätä solua vastaavan argumenttiarvojen joukon funktion arvo N toveri
A) JA b) TAI
Riisi. 8. Esimerkki Karnaugh-kartoista kahden muuttujan funktioille
Karnaughin kartassa And-funktiolle on vain yksi 1, joten sitä ei voi liimata mihinkään. Minimifunktion lauseke sisältää vain tätä 1 vastaavan termin:
f = x y.
TAI-funktion Carnot-kartassa on jo kolme ykköstä ja voit tehdä kaksi tarraparia, joista 1 vastaa termiä xy , käytetään kahdesti. Minimaalisen funktion lausekkeessa sinun on kirjoitettava yhteen liimattavien parien ehdot jättäen niihin kaikki muuttujat, jotka eivät muutu tälle parille, ja poistamalla muuttujat, jotka muuttavat arvoaan. Vaakasuoraan liimaukseen saamme x , ja pystysuoralle y , tuloksena saamme lausekkeen
f = x + y.
Kuvassa 9 näyttää kahden kolmen muuttujan funktion totuustaulukot ( A ) ja heidän Carnot-kartat ( b ja c). Funktio f 2 eroaa ensimmäisestä siinä, että sitä ei ole määritelty kolmelle muuttujajoukolle (taulukossa tämä on merkitty viivalla).
Vähimmäis-DNF-funktiota määritettäessä käytetään seuraavia sääntöjä. Kaikki solut, jotka sisältävät numeron 1, yhdistetään suljetuiksi suorakaiteen muotoisiksi alueiksi, joita kutsutaan k-kuutiot, missä k = log 2 K, K määrä 1 suorakaiteen muotoisella alueella. Tässä tapauksessa jokaisen alueen tulee olla suorakulmio, jonka solujen lukumäärä on 2 k, jossa k = 0, 1, 2, 3, …. Jos k = 1 suorakulmio kutsutaan yksi on kuutio ja sisältää 2 1 = 2 yksikköä; k = 2 suorakulmio sisältää 2 2 = 4 yksikköä ja sitä kutsutaan kahden kuution; kun k = 3 alue 2 3:sta = 8 yksikköä kutsutaan kolmen kuution ; jne. Voidaan kutsua yksiköitä, joita ei voida yhdistää suorakulmioiksi nollakuutiot , jotka sisältävät vain yhden yksikön (2 0 = 1). Kuten voidaan nähdä, jopa k alueet voivat olla neliön muotoisia (mutta ei välttämättä), ja jos ne ovat parittomat k vain suorakulmiot.
|
b c |
||||||
Riisi. 9. Esimerkki Karnaugh-kartoista kolmen muuttujan funktioille
Nämä alueet voivat mennä päällekkäin, eli samat solut voivat päästä eri alueille. Sitten minimi DNF-funktio kirjoitetaan kaikkien vastaavien konjunktiivitermien disjunktioksi k - kuutiot.
Jokainen Karnaugh-kartan osoitetuista alueista on esitetty minimaalisessa DNF:ssä konjunktiolla, jonka argumenttien määrä on k vähemmän kuin funktion argumenttien kokonaismäärä m eli tämä luku on yhtä suuri mk . Jokainen minimaalisen DNF:n konjunktio koostuu vain niistä argumenteista, joilla vastaavalle kartan alueelle on arvoja joko ilman inversioita tai vain inversioiden kanssa, eli ne eivät muuta niiden merkitystä.
Peitettäessä karttasoluja suljetuilla alueilla tulee siis pyrkiä varmistamaan, että alueita on mahdollisimman vähän ja jokainen alue sisältää mahdollisimman monta solua, koska tällöin termien määrä minimi-DNF:ssä on minimaalinen ja argumenttien määrä vastaavassa konjunktiossa on minimaalinen.
Kuvan Karnaugh-kartan mukaiselle funktiolle. 9, b löydämme
koska ylemmän suljetun alueen muuttujat x 1 ja x 2 niillä on arvot ilman inversioita alemmille x 1 merkitystä inversiolla ja x 3 ilman inversiota.
Määrittämättömät arvot kartalla kuvassa. 9, V voidaan määritellä tarkemmin korvaamalla se nollalla tai yhdellä. Tälle funktiolle on selvää, että on kannattavampaa korvata molemmat määrittelemättömät arvot 1:llä. Tässä tapauksessa muodostuu kaksi aluetta, jotka ovat erityyppisiä 2-kuutioita. Sitten DNF-minimifunktion lauseke on seuraava:
Suljettuja alueita rakennettaessa Carnot-kartta saa taittaa sylinteriksi sekä vaaka- että pystysuunnassa. R tikaalikirveitä vastakkaisten kasvojen liitolla R sinä, eli yksiköt, jotka sijaitsevat Carnotin symmetriakartan reunoilla h mutta voidaan myös yhdistää.
Carnaugh-kartat voidaan piirtää eri tavoin (kuva 10).
|
x 2 x 3 |
||||||||||
a b
Riisi. 10. Erilaisia tapoja kuvata Carnaughin karttoja
3 muuttujan funktiolle
Mutta kätevimmät vaihtoehdot Karnaugh-kartoille 2-4 muuttujan funktioille ovat ne, jotka on esitetty kuvassa. 11 taulukkoa, koska ne näkyvät jokaisessa solussa A Meillä on kaikki muuttujat suorassa tai käänteisessä muodossa.
a b
Riisi. yksitoista. Kätevin kuva Carnaugh-kartoista
funktioille 3 ( a) ja 4 (b) muuttujat
5 ja 6 muuttujan funktioille kuvassa 1 esitetty menetelmä. 10, V .
Riisi. 12. Kuva Karnaughin kartasta 5 muuttujan funktiolle
Riisi. 13. Kuva Karnaughin kartasta 6 muuttujan funktiolle
Muita vastaavia teoksia, jotka saattavat kiinnostaa sinua.vshm> |
|||
| 9020. | KAKSIAISUUDEN PERIAATE. BOOLIEN FUNKTIOIEN LAAJENTAMINEN MUUTTUJIHIN. TÄYDELLINEN DISJUNKTIIVINEN JA KONJUNKTIIVINEN NORMAALIMUODOT | 96,34 kt | |
| Tämä lause on luonteeltaan rakentava, koska se sallii jokaisen funktion rakentaa kaavan, joka toteuttaa sen täydellisen d.n:n muodossa. f. Tätä varten merkitsemme kunkin funktion totuustaulukossa kaikki rivit, joilla | |||
| 6490. | Loogisten funktioiden kuvaus ja minimointi | 187,21 kt | |
| Suhde funktion argumenttien ja sen arvojen välillä ilmaistaan sanallisessa muodossa. Esimerkki: Kolmen argumentin funktio saa arvon, kun kaksi tai useampi funktion argumentti on yhtä suuri. Koostuu totuustaulukon muodostamisesta, joka sisältää funktioarvot kaikille argumenttiarvojoukoille. Tässä esimerkissä saamme totuustaulukkoa käyttämällä seuraavan merkinnän muodossa DNF... | |||
| 6707. | Relaatiotietokantojen suunnittelu. Suunnitteluongelmat klassisessa lähestymistavassa. Normalisoinnin periaatteet, normaalimuodot | 70,48 kt | |
| Mikä on relaatiotietokantaprojekti Tämä on joukko toisiinsa kytkettyjä suhteita, joissa määritellään kaikki attribuutit, määritetään suhteiden ensisijaiset avaimet ja määritetään joitain suhteiden lisäominaisuuksia, jotka liittyvät eheyden ylläpitämisen periaatteisiin. Siksi tietokannan suunnittelun on oltava erittäin tarkka ja varmennettu. Itse asiassa tietokantaprojekti on perusta tulevalle ohjelmistopaketille, jota käytetään melko pitkään ja monien käyttäjien keskuudessa. | |||
| 4849. | Tilatoimintojen toteutusmuodot ja menetelmät | 197,3 kt | |
| Termillä ”toiminto” ei ole läheskään samaa merkitystä kotimaisessa ja ulkomaisessa tieteellisessä kirjallisuudessa. Filosofisesti ja yleissosiologisesti sitä pidetään "esineen ominaisuuksien ulkoisena ilmentymänä tietyssä suhdejärjestelmässä"; joukkona yksilöiden tai elinten tavallisia tai erityisiä toimia | |||
| 17873. | Loogisen UUD:n muodostaminen 3. luokan oppilaille | 846,71 kt | |
| Psykologiset ja pedagogiset näkökohdat loogisten universaalien toimien muodostumisongelmassa alakouluikäisillä Menetelmät loogisten UUD:iden muodostumisen arviointiin. Yleisen koulutusjärjestelmän yleisen koulutustoiminnan kehittämiskonseptin kehittäminen vastaa uusiin yhteiskunnallisiin tarpeisiin. Nykyaikaisen koulutusjärjestelmän tärkein tehtävä on UUD:n yleismaailmallisen koulutustoiminnan muodostaminen. Yleismaailmallisen koulutustoiminnan muodostuminen on avain kouluvaikeuksien ehkäisyyn. | |||
| 2638. | Loogisten yhteyksien tekninen toteutus automaattisissa estojärjestelmissä | 1,04 Mt | |
| Loogisten kytkentöjen tekninen toteutus automaattisissa estojärjestelmissä Kolmi- ja nelinumeroisten akkujen ohjausalgoritmien tekninen toteutus voidaan toteuttaa käyttämällä relekontaktia ja kontaktittomia diskreettejä ja integroituja logiikkaelementtejä... | |||
| 10203. | RISKIKESKEISEN LÄHESTYMISTAVAN KÄSITTEEN SOVELTAMINEN HÄTÄTILANTEIDEN JA KEHITTYMISEN RAKENTEELLISTEN JA LOOGISTEN MALLIEN RAKENNUSTA | 70,8 kt | |
| Yleinen riskianalyysi Tuotantoympäristö on kyllästynyt tehokkailla teknologisilla järjestelmillä ja teknologioilla, jotka tekevät ihmisen työstä tuottavaa ja fyysisesti vähemmän vaikeaa, mutta vaarallisempaa. Riskille on ominaista vaaratilanteen alkamisen odottamattomuus ja äkillisyys. Joka päivä kohtaamme lukuisia riskejä, mutta suurin osa niistä säilyy mahdollisina Riskiteoria antaa kvantitatiivisen arvion ihmiseen kohdistuvista kielteisistä vaikutuksista sekä hänen terveydelle ja hengelle aiheutuvista vahingoista. | |||
| 11576. | Liiketoimien käsite, tyypit ja muodot. Vaaditun liiketoimimuodon noudattamatta jättämisen seuraukset | 49,82 kt | |
| Tapahtuman tunnistaminen pätemättömäksi; virheellisten tapahtumien tyypit. Kurssityön sovellettu arvo on transaktion käsitteen yksinkertaistamisessa eli sen julkisessa esittämisessä helpommin saavutettavissa olevassa muodossa. | |||
| 6213. | Funktion approksimaatio | 3,08 Mt | |
| Ensimmäinen koostuu tietyn analyyttisesti tai taulukkomuodossa määritellyn funktion korvaamisesta toisella funktiolla, joka on lähellä alkuperäistä mutta yksinkertaisempaa ja laskelmien kannalta kätevämpää. Esimerkiksi korvaamalla funktion polynomilla voit saada yksinkertaisia kaavoja numeerista integrointia ja differentiointia varten; Taulukon korvaaminen likimääräisellä funktiolla mahdollistaa arvojen saamisen sen välipisteissä. Toinen ongelma syntyy myös: tietyn segmentin funktion palauttaminen tälle segmentille annetuista funktion arvoista erillisessä pistejoukossa. Vastaus tähän kysymykseen... | |||
| 14058. | Valtion toimintojen kehitys | 29,99 kt | |
| Venäjän valtion on oikeudellisena ilmiönä ennen kaikkea varmistettava valtion tarkoituksen toteutuminen sekä sen tärkeimmät perustuslailliset ominaispiirteet demokraattisena liittovaltion oikeudellisena sosiaalisena maallisena valtiona, jolla on tasavaltainen hallintomuoto. Valtion päätarkoitus määräytyy art. | |||
Esimerkki. Etsi CNF-kaavat ![]()
~ ![]() ~
~
![]()
SDNF:n täydellinen disjunktiivinen normaalimuoto voidaan rakentaa käyttämällä seuraavaa algoritmia:
1. = 1. DNF-algoritmi
2. = 2. DNF-algoritmi
3. = 3. DNF-algoritmi
4. = 4. DNF-algoritmi
5. Jätä pois identtiset väärät termit, eli lomakkeen termit
6. Täydennä loput termit puuttuvilla muuttujilla
7. Toista kohta 4.
Esimerkki. Etsi SDNF-kaavat.
![]() ~
~
![]()
![]()
![]()
![]()
SCNF:n rakentamiseen voit käyttää seuraavaa kaaviota:
Esimerkki. Etsi SDNF-kaavat.
![]() ~
~
![]()
Tiedetään (Lauseet 2.11, 2.12), että SDNF ja SCNF määritellään yksiselitteisesti kaavalla ja siksi ne voidaan konstruoida käyttämällä kaavan totuustaulukkoa.
Kaava SDNF:n ja SCNF:n rakentamiseksi totuustaulukon mukaan on annettu alla kaavalle ![]() ~ :
~ :
| | ||||
| 1 0 1 0 1 1 0 1 | SDNF; SKNF. |
2.2. Harjoittele.
2.2.1 Alla on Boolen lausekkeet. Yksinkertaista muunnelmasi lausekkeet mahdollisimman paljon käyttämällä Boolen logiikan lakeja. Käytä sitten totuustaulukoita vertaillaksesi yksinkertaistettua lausekettasi alkuperäiseen.






2.2.2. Selvitä kysymys f 1:n ja f 2:n vastaavuudesta vähentämällä ne SDNF:ksi (taulukko 1).
2.2.3. Etsi f 3:n kaksoisfunktio käyttämällä yleistettyä ja Boolen periaatetta (taulukko 1). Vertaa tuloksia.
| № | f 1 | f 2 | f 3 |
| | |||
| |
|||
| | |||
| | |||
| | |||
| | |
||
| | |
||
| |
|||
| | |||
| | |||
| |
|||
| | |||
| | |
||
| | |||
| |
2.3. Kontrollikysymykset.
2.3.1. Määrittele lausunto.
2.3.2. Listaa lausunnon päätoiminnot.
2.3.3. Mikä on totuustaulukko?
2.3.4. Luo totuustaulukot seuraaville kaavoille:
~ ~ ![]() ~ ;
~ ;
2.3.5. Ottaen huomioon operaatioiden järjestystä koskevat käytännöt, jätä kaavoista pois "ylimääräiset" sulkeet ja " "-merkki:
![]() ;
;
2.3.6. Todista kaavojen identtinen totuus käyttämällä ekvivalentteja muunnoksia:
2.3.7. Etsi kaksoiskaavat:
![]()
![]()
![]() )
)
2.3.8. Pienennä seuraavat kaavat täydelliseen DNF (SDNF) muotoon:
![]() ~
~
2.3.9. Pienennä seuraavat kaavat täydelliseen CNF (SCNF) muotoon:
![]()
![]() ~
~
![]()
![]()
Laboratoriotyö nro 3
Aihe:"Boolen funktioiden minimointi. Logiikka"
Kohde: Hankitaan käytännön taitoja työskennellä Boolen funktioiden minimointimenetelmien kanssa.
3.1. Teoreettista tietoa.
Minimaaliset muodot
Kuten näytettiin, mikä tahansa Boolen funktio voidaan esittää täydellisessä normaalimuodossa (disjunktiivi tai konjunktiivi). Lisäksi tällainen esitys on ensimmäinen askel siirtymisessä funktion taulukkomäärittelystä sen analyyttiseen ilmaisuun. Seuraavassa edetään disjunktiivimuodosta, ja vastaavat tulokset konjunktiivimuodolle saadaan kaksinaisuuden periaatteen perusteella.
Kanoninen ongelma loogisten piirien syntetisoinnissa Boolen pohjalta tiivistyy Boolen funktioiden minimoimiseen, ts. esittää ne disjunktiivisessa normaalimuodossa, joka sisältää pienimmän määrän kirjaimia (muuttujia ja niiden negatiivisia). Tällaisia muotoja kutsutaan minimaaliksi. Kanonisessa synteesissä oletetaan, että sekä signaalit että niiden inversiot syötetään piirin tuloihin.
Disjunktiivisessa normaalimuodossa esitettyä kaavaa yksinkertaistetaan käyttämällä toistuvasti liimausoperaatiota ja absorptiooperaatiota ja (konjunktiivisen normaalimuodon kaksoisidentiteetit ovat muotoa: ja ). Tässä ja voidaan ymmärtää minkä tahansa Boolen algebran kaavana. Tuloksena päästään analyyttiseen lausekkeeseen, jossa muut muunnokset eivät ole enää mahdollisia, ts. saamme umpikujamuodon.
Umpikujamuotojen joukossa on myös minimaalinen disjunktiivinen muoto, eikä se välttämättä ole ainutlaatuinen. Varmistaaksesi, että tietty umpikujalomake on minimaalinen, sinun on löydettävä kaikki umpikujalomakkeet ja verrattava niitä niiden sisältämien kirjainten lukumäärän mukaan.
Oletetaan esimerkiksi funktio täydellisessä normaalissa disjunktiivimuodossa:
Ryhmittelemällä termit ja soveltamalla liimausoperaatiota meillä on .
Toisella ryhmittelymenetelmällä saamme:
Molemmat umpikujamuodot eivät ole minimaalisia. Minimaalisen muodon saamiseksi sinun on arvattava toistaaksesi yksi termi alkuperäisessä kaavassa (tämän voi aina tehdä, koska ). Ensimmäisessä tapauksessa tällainen jäsen voi olla . Sitten . Lisäämällä termin , saamme: . Kun olet käynyt läpi kaikki mahdolliset vaihtoehdot, voit varmistaa, että kaksi viimeistä muotoa ovat minimaaliset.
Kaavojen kanssa työskentely tällä tasolla on kuin vaeltelua pimeässä. Minimaalisten muotojen etsintäprosessista tulee visuaalisempi ja tarkoituksenmukaisempi, jos käyttää joitain graafisia ja analyyttisiä esityksiä ja symboleita, jotka on erityisesti kehitetty tähän tarkoitukseen.
Moniulotteinen kuutio
Jokainen -ulotteisen kuution kärki voidaan liittää yksikön ainesosaan. Näin ollen merkittyjen pisteiden osajoukko on täydellisessä disjunktiivisessa normaalimuodossa olevien muuttujien Boolen funktion -ulotteisen kuution kartoitus. Kuvassa 3.1 esittää tällaisen funktion kuvauksen lausekkeesta 3.7.

Kuva 3.1 SDNF:ssä esitetyn funktion näyttö kolmiulotteisessa kuutiossa
Missä tahansa disjunktiivisessa normaalimuodossa esitettyjen muuttujien funktion näyttämiseksi on tarpeen luoda vastaavuus sen minitermien ja -ulotteisen kuution elementtien välille.
(-1) arvosanan minitermiä voidaan pitää tuloksena liimaamalla yhteen kaksi arvosanaa (yksinäisyyden ainesosa), ts. ![]() , -ulotteisessa kuutiossa tämä vastaa kahden sellaisen kärjen korvaamista, jotka eroavat vain koordinaatin arvoista, jotka yhdistävät nämä kärjet reunaan (reunan sanotaan peittävän siihen tulevat kärjet). Siten (-1):nnen kertaluvun minitermit vastaavat -ulotteisen kuution reunoja. Vastaavasti (-2) kertaluvun minitermien vastaavuus määritetään -ulotteisen kuution pintojen kanssa, joista jokainen peittää neljä kärkeä (ja neljä reunaa).
, -ulotteisessa kuutiossa tämä vastaa kahden sellaisen kärjen korvaamista, jotka eroavat vain koordinaatin arvoista, jotka yhdistävät nämä kärjet reunaan (reunan sanotaan peittävän siihen tulevat kärjet). Siten (-1):nnen kertaluvun minitermit vastaavat -ulotteisen kuution reunoja. Vastaavasti (-2) kertaluvun minitermien vastaavuus määritetään -ulotteisen kuution pintojen kanssa, joista jokainen peittää neljä kärkeä (ja neljä reunaa).
-ulotteisen kuution elementtejä, joille on tunnusomaista mitat, kutsutaan -kuutioiksi. Siten kärjet ovat 0-kuutiot, reunat 1-kuutiot, pinnat ovat 2-kuutiot jne. Yleistäen yllä olevaa päättelyä, voidaan olettaa, että ():nnen asteen minitermi disjunktiivisessa normaalimuodossa muuttujien funktiolle esitetään -kuutiolla, ja jokainen -kuutio kattaa kaikki ne pienemmän ulottuvuuden -kuutiot, jotka liittyvät sen kärkiin. . Esimerkkinä kuvassa. 3.2 esittää kolmen muuttujan funktiota. Tässä minitermit vastaavat 1-kuutiota (), ja minitermiä edustaa 2-kuutio ().

Kuva 3.2 Toiminnon kattavuus ![]()
Joten mikä tahansa disjunktiivinen normaalimuoto kartoitetaan -ulotteiseen kuutioon joukolla -kuutioita, jotka kattavat kaikki yksikön aineosia vastaavat kärjet (0-kuutiot). Myös käänteinen väite on totta: jos tietty joukko -kuutioita kattaa joukon kaikkia funktion yksikköarvoja vastaavia pisteitä, niin näitä -kuutioita vastaavien minitermien disjunktio on tämän funktion lauseke disjunktiivisessa normaalissa. muodossa. Tällaisen kokoelman -kuutioita (tai niitä vastaavia minitermejä) sanotaan muodostavan funktion peitteen.
Minimaalisen muodon halu ymmärretään intuitiivisesti sellaisen päällysteen etsimiseksi, jonka kuutioiden määrä olisi pienempi ja niiden mitat suurempi. Minimimuotoa vastaavaa kattavuutta kutsutaan minimikattavuudeksi. Esimerkiksi kuvan 1 peittotoiminnolle. 3.3 täyttää vähimmäislomakkeet ![]() Ja
Ja ![]() .
.

Riisi. 3.3 Toimintojen kattavuus.
vasemmalle – ![]() ; oikealla –
; oikealla – ![]()
 Toiminnon näyttäminen -ulotteisessa kuutiossa on selkeä ja yksinkertainen, kun . Neliulotteinen kuutio voidaan kuvata kuvan 1 mukaisesti. 3.4, joka näyttää neljän muuttujan funktion ja sen lauseketta vastaavan minimikattavuuden
Toiminnon näyttäminen -ulotteisessa kuutiossa on selkeä ja yksinkertainen, kun . Neliulotteinen kuutio voidaan kuvata kuvan 1 mukaisesti. 3.4, joka näyttää neljän muuttujan funktion ja sen lauseketta vastaavan minimikattavuuden ![]() . Tämän menetelmän käyttö vaatii niin monimutkaisia rakenteita, että kaikki sen edut menetetään.
. Tämän menetelmän käyttö vaatii niin monimutkaisia rakenteita, että kaikki sen edut menetetään.
Riisi. 3.4 Toimintojen näyttö ![]() neliulotteisessa kuutiossa
neliulotteisessa kuutiossa
Carnot kartat
Toinen menetelmä Boolen funktioiden graafiseen esittämiseen käyttää Carnot kartat, jotka ovat erityisesti järjestettyjä vastaavuustaulukoita. Taulukon sarakkeet ja rivit vastaavat kaikkia mahdollisia enintään kahden muuttujan arvojoukkoja, ja nämä joukot on järjestetty sellaiseen järjestykseen, että jokainen seuraava eroaa edellisestä vain yhden muuttujan arvossa. . Tämän ansiosta taulukon viereiset solut vaakasuunnassa ja pystysuunnassa eroavat vain yhden muuttujan arvosta. Taulukon reunoilla sijaitsevat solut katsotaan myös viereisiksi ja niillä on tämä ominaisuus. Kuvassa Kuva 3.5 näyttää Karnaugh-kartat kahdelle, kolmelle, neljälle muuttujalle.
 |
|||||
 |
|||||
 |
|||||
Riisi. 3.5 Carnaugh-kartat kahdelle, kolmelle ja neljälle muuttujalle
Kuten tavallisissa totuustaulukoissa, niiden joukkojen solut, joissa funktio saa arvon 1, täytetään ykkösillä (nollat eivät yleensä mahdu, ne vastaavat tyhjiä soluja). Esimerkiksi kuvassa Fig. 3.6, A esittää Karnaugh-kartan funktiolle, jonka näyttö neliulotteisessa kuutiossa on esitetty kuvassa 1. 3.4. Asioiden yksinkertaistamiseksi rivit ja sarakkeet, jotka vastaavat muuttujan arvoa 1, on korostettu tätä muuttujaa osoittavalla aaltosululla.
 |
|||
 |
|||
Riisi. 3.6 Neljän muuttujan funktion näyttäminen Carnaugh-kartalla
(a) ja sen vähimmäissuoja (b)
Funktiokartoitusten välillä n-ulotteinen kuutio ja Carnot-kartta ovat yksi-yhteen vastaavuus. Carnotin kartalla s-kuutio vastaa 2 vierekkäisen solun joukkoa, jotka on sijoitettu riviin, sarakkeeseen, neliöön tai suorakulmioon (ottaen huomioon kartan vastakkaisten reunojen läheisyyden). Siksi kaikki edellä mainitut määräykset (katso kohta. moniulotteinen kuutio), ovat voimassa Karnaugh-kartoissa. Joten kuvassa 3.6, b näyttää minimidisjunktiivimuotoa vastaavien karttayksiköiden kattavuuden ![]() kyseessä oleva toiminto.
kyseessä oleva toiminto.
Minitermien lukeminen Karnaugh-kartalta noudattaa yksinkertaista sääntöä. Solujen muodostuminen s-kuutio, anna miniter (n–s)-th rank, joka sisältää ne (n–s) muuttujat, jotka säilyttävät samat arvot tässä s-kuutio, jossa arvo 1 vastaa itse muuttujia ja arvo 0 vastaa niiden negaatioita. Muuttujat, jotka eivät säilytä arvojaan s-kuutio, ovat poissa minitermissä. Erilaiset lukutavat johtavat funktion erilaisiin esityksiin disjunktiivisessa normaalimuodossa (oikealla oleva minimaalinen) (kuva 3.7).
 |  |
||||||||
 |
|||||||||
Karnaugh-karttojen käyttö vaatii yksinkertaisempia rakenteita verrattuna kartoitukseen n-ulotteinen kuutio, erityisesti neljän muuttujan tapauksessa. Viiden muuttujan funktioiden näyttämiseksi käytetään kahta Karnaugh-karttaa neljälle muuttujalle ja kuuden muuttujan funktiolle neljää tällaista karttaa. Muuttujien määrän lisääntyessä Karnaugh-kartoista tulee käytännössä käyttökelvottomia.
Kuuluisa kirjallisuudessa Veitch-kortit Ne eroavat vain muuttujaarvojoukkojen eri järjestyksessä ja niillä on samat ominaisuudet kuin Karnaugh-kartoilla.
Kuutioiden kompleksi
Graafisten menetelmien epäjohdonmukaisuus suurella määrällä muuttujia kompensoidaan erilaisilla analyyttisilla menetelmillä Boolen funktioiden esittämiseksi. Yksi tällainen esitys on kuutioiden kompleksi, jossa käytetään moniulotteisen loogisen tilan terminologiaa yhdistettynä erityisesti kehitetyn symboliikkaan.
). 0-kuutiot, jotka vastaavat yhtenäisyyden ainesosia, esitetään muuttuja-arvojoukoilla, joilla funktio on yhtä suuri kuin yksikkö. Ilmeisesti äänityksessä


Riisi. 3.8 Kolmen muuttujan funktion kuutioiden kompleksi ( A) ja sen symbolinen esitys ( b)
Kuutioiden kompleksi muodostuu maksimaalinen toimintopeitto. Sulkemalla pois kaikki nuo s-kuutiot, jotka on peitetty korkeamman ulottuvuuden kuutioilla, saadaan umpikujamuotoja vastaavat päällysteet. Tarkasteltavalle esimerkille (kuva 3.8) on siis umpikuja
 ,
,
joka vastaa toimintoa ![]() . Tässä tapauksessa tämä kattavuus on minimaalinen.
. Tässä tapauksessa tämä kattavuus on minimaalinen.
Kahden Boolen funktion disjunktiooperaatio vastaa niiden kuutiokompleksien liittoa ja konjunktiooperaatio vastaa niiden kuutiokompleksien leikkauskohtaa. Funktion negaatio vastaa kuutiokompleksin komplementtia, eli sen määräävät kaikki kärjet, joissa funktio saa arvon 0. Siten funktion algebran välillä on yksi yhteen vastaavuus (isomorfismi). Boolen funktiot ja Boolen joukot, jotka edustavat kuutioiden komplekseja.
Funktion esittäminen kuutiokompleksien muodossa on vähemmän visuaalista, mutta sen tärkeimmät edut ovat muuttujien lukumäärän rajoitusten poistaminen ja tiedon koodaus helpottuu tietokoneita käytettäessä.
Boolen funktioiden minimoiminen
Ongelman muotoilu. Piirin minimointi Boolen perusteella tarkoittaa, että löydetään vähimmäiskattavuutta vastaava vähimmäisdisjunktiivimuoto. Normaalimuodossa olevien kirjeiden kokonaismäärä ilmaistaan peittokuluina ![]() , missä on niiden kuutioiden lukumäärä, jotka muodostavat tietyn n muuttujan funktion peitteen. Minimikattavuudelle on ominaista sen hinnan alhaisin arvo.
, missä on niiden kuutioiden lukumäärä, jotka muodostavat tietyn n muuttujan funktion peitteen. Minimikattavuudelle on ominaista sen hinnan alhaisin arvo.
Tyypillisesti minimointiongelma ratkaistaan kahdessa vaiheessa. Ensin etsimme pienennettyä kantta, joka sisältää kaikki maksimimittaiset -kuutiot, mutta ei sisällä ainuttakaan kuutiota, jonka yksikään tämän kannen kuutio peittää. Vastaavaa disjunktiivista normaalimuotoa kutsutaan pelkistetyksi ja sen minitermejä yksinkertaisiksi implikantteiksi. Tietylle toiminnolle alennettu peitto on ainutlaatuinen, mutta se voi olla tarpeeton, koska osa kuutioista on muiden kuutioiden kokoelman peitossa.
Toisessa vaiheessa siirrytään pelkistetyistä disjunktiivisista normaalimuodoista umpikujaan, joista valitaan minimaaliset muodot. Umpikujamuodot muodostetaan jättämällä pois supistetusta kattavuudesta kaikki ylimääräiset kuutiot, joita ilman jäljellä oleva kuutiojoukko muodostaa edelleen tietyn funktion peitteen, mutta jos jokin kuutioista edelleen jätetään pois, se ei enää kata kaikkien kuutioiden joukkoa. funktion yksittäisiä arvoja vastaavat kärjet, eli se lakkaa olemasta peitto .
Pienennetty peittokuutio, joka kattaa tietyn funktion kärjet, joita muut kuutiot eivät peitä, ei voi olla redundantti, ja se sisällytetään aina vähimmäispeittoon. Tällaista kuutiota, kuten sen vastaavaa implikanttia, kutsutaan äärimmäiseksi (olennainen implikantti), ja sen peittämiä kärkipisteitä kutsutaan peruutetuiksi pisteiksi. Extremaalien joukko muodostaa päällysteen ytimen, on selvää, että siirryttäessä supistetusta kattavuudesta minimaaliseen tulee ensinnäkin eristää kaikki ääripäät. Jos ääripääjoukko ei muodosta peitettä, sitä täydennetään peittämällä kuutioilla pelkistetystä päällysteestä.
Annetut määritelmät on havainnollistettu kuvassa. 3.9, jossa kattavuus on pienempi (katso kuva 3.9a, ) ja vähimmäispeitot (kuva 3.9b) ja (katso kuva 3.9, b) ilmaistaan seuraavasti.