1 ja 2 johdannaisten mekaaninen merkitys. Toisen asteen derivaatta ja sen mekaaninen merkitys. Johdannan geometrinen, mekaaninen, taloudellinen merkitys
Johdannan mekaaninen merkitys
Derivaatan mekaanisen tulkinnan antoi ensimmäisenä I. Newton. Se koostuu seuraavasta: aineellisen pisteen liikkeen nopeus tietyllä ajanhetkellä on yhtä suuri kuin reitin derivaatta ajan suhteen, ts. Jos siis aineellisen pisteen liikelaki on annettu yhtälöllä, niin pisteen hetkellisen nopeuden löytämiseksi jossakin tietty hetki aikaa, sinun on löydettävä derivaatta ja korvattava siihen vastaava t:n arvo.
Toisen asteen derivaatta ja sen mekaaninen merkitys
Saamme (yhtälön siitä, mitä tehtiin oppikirjassa Lisichkin V.T. Soloveychik I.L. "Mathematics" s. 240):
Täten, kiihtyvyys suoraviivaista liikettä kappale tietyllä hetkellä on yhtä suuri kuin polun toinen derivaatta ajan suhteen, laskettuna tälle hetkelle. Tämä on toisen derivaatan mekaaninen merkitys.
Differentiaalin määritelmä ja geometrinen merkitys
Määritelmä 4. Pääosa funktion inkrementistä, lineaarinen suhteessa funktion kasvuun, lineaarinen riippumattoman muuttujan inkrementin suhteen, on ns. ero toimii ja on merkitty d:llä, ts. .
Funktion differentiaali esitetään geometrisesti pisteessä M (x; y) piirretyn tangentin ordinaatin lisäyksellä annetuille x:n ja ?x:n arvoille.
laskeminen ero - .
Differentiaalin soveltaminen likimääräisissä laskelmissa - , funktion inkrementin likimääräinen arvo on sama kuin sen differentiaali.
Lause 1.Jos differentioituva funktio kasvaa (vähenee) tietyllä aikavälillä, niin tämän funktion derivaatta ei ole negatiivinen (ei positiivinen) tällä välillä.
Lause 2.Jos johdannainen funktio on positiivinen (negatiivinen) jossain välissä, niin tämän intervallin funktio on monotonisesti kasvava (monotonisesti laskeva).
Muotoilkaamme nyt sääntö funktion monotonisuuden intervallien löytämiseksi
1. Laske tämän funktion derivaatta.
2. Etsi pisteet, joissa se on nolla tai ei ole olemassa. Näitä pisteitä kutsutaan kriittinen toimintoa varten
3. Löytyneiden pisteiden avulla funktion alue jaetaan intervalleihin, joissa jokaisessa derivaatta säilyttää etumerkkinsä. Nämä intervallit ovat monotonisuuden intervalleja.
4. Tutki jokaisen löydetyn intervallin merkkiä. Jos tarkasteluvälillä, niin tällä aikavälillä kasvaa; jos, niin se pienenee sellaisella aikavälillä.
Ongelman ehdoista riippuen sääntöä monotonisuusvälien löytämiseksi voidaan yksinkertaistaa.
Määritelmä 5. Pistettä kutsutaan funktion maksimi- (minimi)pisteeksi, jos epäyhtälö pätee vastaavasti mille tahansa x:lle pisteen jostain naapurustosta.
Jos on funktion maksimi (minimi) -piste, niin he sanovat sen (minimi) pisteessä. Maksimi- ja minimifunktiot yhdistävät nimen ääripää funktioita, ja maksimi- ja minimipisteet kutsutaan ääripisteet (ääripisteet).
Lause 3.(välttämätön merkki ääripäästä). Jos on funktion ääripiste ja derivaatta on olemassa tässä pisteessä, niin se on yhtä suuri kuin nolla: .
Lause 4.(riittävä merkki ääripäästä). Jos derivaatan etumerkki muuttuu, kun x kulkee a:n kautta, niin a on funktion ääripiste.
Johdannan tutkimuksen pääkohdat:
1. Etsi derivaatta.
2. Löydä kaikki kriittiset kohdat toiminnon laajuudesta.
3. Aseta funktion derivaatan etumerkit ajaessasi kriittisten pisteiden läpi ja kirjoita ääripisteet.
4. Laske funktioarvot kussakin ääripisteessä.
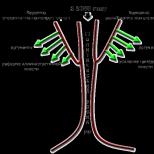
Antaa aineellinen kohta M liikkuu lain mukaan suorassa linjassa S = f(t). Kuten jo tiedetään, johdannainen S t' yhtä suuri kuin pisteen nopeus tietyllä hetkellä: S t '= V.
Anna tällä hetkellä t pisteen nopeus on V, ja tällä hetkellä t+Dt – nopeus on V+DV, eli jonkin aikaa Dt nopeus on muuttunut DV.
Suhde ilmaisee keskikiihtyvyyden pisteen liike aikana Dt. Tämän suhteen raja on Dt®0 kutsutaan pisteen kiihtyvyydeksi M Tällä hetkellä t ja se on merkitty kirjaimella V: ![]() Niin, reitin toinen derivaatta ajan suhteen on pisteen suoraviivaisen liikkeen kiihtyvyyden arvo, eli .
Niin, reitin toinen derivaatta ajan suhteen on pisteen suoraviivaisen liikkeen kiihtyvyyden arvo, eli .
Korkeamman asteen erot
Antaa y=f(x) differentioituva funktio ja sen argumentti X on riippumaton muuttuja. Silloin sen ensimmäinen differentiaali on myös funktio X, voimme löytää tämän funktion differentiaalin.
Differentiaalia funktion differentiaalista kutsutaan sen toiseksi differentiaaliksi (tai toisen asteen differentiaaliksi) ja sitä merkitään : .
Tietyn funktion toisen asteen differentiaali on yhtä suuri kuin tämän funktion toisen kertaluvun tulo ja riippumattoman muuttujan differentiaalin neliö: ![]() .
.
Differentiaalilaskennan soveltaminen
Funktiota kutsutaan kasvaa (vähenee)) välissä (
a; b)
jos kahdelle pisteellex 1
Jax2
määritellyltä väliltä, joka täyttää epäyhtälön , epätasa-arvo täyttyy ![]() (
(![]() ).
).
Tarpeellinen kunto nouseva laskeva): Jos vaihteluvälin funktio ( a, b) kasvaa (vähenee), silloin tämän funktion derivaatta on ei-negatiivinen (ei-positiivinen) tällä välillä() .
Riittävä edellytys lisääntymiselle (vähentämiselle):Jos differentioituvan funktion derivaatta on positiivinen (negatiivinen) jollain aikavälillä, niin funktio kasvaa (pienenee) tällä välillä.
Toiminto f(x) pisteessä x 1 Sillä on enimmäismäärä, jos jollekin X f(x 1)>f(x), klo x ¹ x 1 .
Toiminto f(x) pisteessä x 1 Sillä on minimi, jos jollekin X jostain pisteen läheisyydestä pätee seuraava epäyhtälö: f(x1)
Funktion ääripäätä kutsutaan paikalliseksi ääripääksi, koska ääripään käsite liittyy vain pisteen x 1 riittävän pieneen ympäristöön. Joten yhdellä intervallilla funktiolla voi olla useita ääriarvoja, ja voi käydä niin, että minimi yhdessä pisteessä on suurempi kuin maksimi toisessa. Maksimin tai minimin esiintyminen intervallin erillisessä pisteessä ei tarkoita, että tässä vaiheessa funktio f(x) ottaa suurimman tai pienimmän arvon tällä aikavälillä.
Välttämätön ääripääehto: Differentioituvan funktion ääripisteessä sen derivaatta on yhtä suuri kuin nolla.
Riittävä ääripääehto: Jos differentioituvan funktion derivaatta jossain pisteessä x 0 on yhtä suuri kuin nolla ja muuttaa etumerkkiään kulkiessaan tämän arvon läpi, niin luku f (x 0) on funktion ääriarvo, ja jos etumerkki muuttuu plussasta miinukseen, sitten maksimi, jos miinuksesta plussaan, niin minimi.
Pisteitä, joissa jatkuvan funktion derivaatta on nolla tai ei ole olemassa, kutsutaan kriittisiksi.
Funktion tutkiminen ääripäähän tarkoittaa sen kaikkien ääripäiden löytämistä. Sääntö funktion tutkimiseksi ääripäälle:
1). Etsi funktion kriittiset pisteet y = f(x) ja valitse niistä vain ne, jotka ovat funktion alueen sisäisiä pisteitä;
2). Tutki derivaatan merkkiä f"(x) kunkin valitun kriittisen pisteen vasemmalla ja oikealla puolella;
3). Riittävän ääripääehdon perusteella kirjoita ääripisteet (jos sellaisia on) ja laske niistä funktioarvot.
Löytääkseen suurin ja pienin arvo toimintoja segmentillä, on suoritettava useita vaiheita:
1). Selvitä funktion kriittiset virrat ratkaisemalla yhtälö f'(x)=0.
2). Jos kriittiset pisteet osuvat segmenttiin, on tarpeen löytää arvot kriittisistä pisteistä ja intervallin rajoista. Jos kriittiset pisteet eivät osu janalle (tai niitä ei ole olemassa), funktion arvot löytyvät vain janan rajoista.
3). Saatuista funktion arvoista valitaan suurin ja pienin ja vastaus kirjoitetaan esimerkiksi muodossa: ![]() ;
; ![]() .
.
Ongelmanratkaisu
Esimerkki 2.1. Etsi funktion differentiaali: ![]() .
.
Ratkaisu. Toimintodifferentiaalin ominaisuuden 2 ja differentiaalin määritelmän perusteella meillä on:
Esimerkki 2.2. Etsi funktion differentiaali: ![]()
Ratkaisu. Funktio voidaan kirjoittaa muodossa: , . Sitten meillä on:
Esimerkki 2.3. Etsi funktion toinen derivaatta: ![]()
Ratkaisu. Muunnetaan funktio.
Etsitään ensimmäinen johdannainen:
etsi toinen johdannainen:
 .
.
Esimerkki 2.4. Etsi funktion toisen asteen differentiaali ![]() .
.
Ratkaisu. Etsitään toisen asteen differentiaali laskennan lausekkeen perusteella:
Etsitään ensin ensimmäinen johdannainen:
; etsi toinen derivaatta: .
Esimerkki 2.5. Etsi abskissapisteeseen piirretyn käyrän tangentin kaltevuus x=2 .
Ratkaisu. Derivaatan geometrisen merkityksen perusteella meillä on, että kulmakerroin on yhtä suuri kuin funktion derivaatta pisteessä, jonka abskissa on yhtä suuri kuin X
. Etsitään ![]() .
.
Laske - funktion kaavion tangentin kaltevuus.
Esimerkki 2.6. Bakteeripopulaatio tietyllä hetkellä t (t tunneissa mitattuna) ![]() yksilöitä. Selvitä bakteerien kasvunopeus. Selvitä bakteerien kasvunopeus tietyllä hetkellä t = 5 tuntia.
yksilöitä. Selvitä bakteerien kasvunopeus. Selvitä bakteerien kasvunopeus tietyllä hetkellä t = 5 tuntia.
Ratkaisu. Bakteeripopulaation kasvunopeus on ensimmäinen johdannainen ajan suhteen t: .
Jos t = 5 tuntia sitten. Siksi bakteerien kasvunopeus on 1000 yksilöä tunnissa.
Esimerkki 2.7. Kehon reaktio annettuun lääkkeeseen voi ilmetä verenpaineen nousuna, kehon lämpötilan laskuna, pulssin muutoksena tai muina fysiologisina indikaattoreina. Reaktion aste riippuu määrätystä lääkkeen annoksesta. Jos X ilmaisee määrätyn lääkkeen annoksen ja reaktioasteen klo kuvataan funktiolla ![]() . Millä arvolla X suurin vastaus?
. Millä arvolla X suurin vastaus?
Ratkaisu. Etsitään johdannainen ![]() .
.
Etsitään kriittiset kohdat: ⇒ ![]() . ⇒ Siksi meillä on kaksi kriittistä kohtaa:
. ⇒ Siksi meillä on kaksi kriittistä kohtaa: ![]() . Arvo ei täytä ongelman ehtoa.
. Arvo ei täytä ongelman ehtoa.
Etsitään toinen derivaatta ![]() . Lasketaan toisen derivaatan arvo kohdassa .
. Lasketaan toisen derivaatan arvo kohdassa .  . Siksi annostaso antaa suurimman vasteen.
. Siksi annostaso antaa suurimman vasteen.
Esimerkkejä itseratkaisusta
Etsi funktion differentiaali:
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
4. ![]()
Etsi seuraavien funktioiden toiset derivaatat:
6. ![]() .
.
Etsi toisen asteen derivaatat ja kirjoita toisen asteen differentiaalit seuraaville funktioille:
9. ![]() .
.
11. Tutki funktiota ääripäihin asti.
12. Etsi funktion suurin ja pienin arvo ![]() segmentillä.
segmentillä.
13. Etsi funktion kasvu- ja laskuvälit, maksimi- ja minimipisteet sekä akselien leikkauspisteet: ![]()
14. Pisteen liikkeen lailla on muoto ![]() . Määritä tämän pisteen nopeuden ja kiihtyvyyden laki.
. Määritä tämän pisteen nopeuden ja kiihtyvyyden laki.
15. Pisteen liikeyhtälö on muotoa (m). Selvitä 1) pisteen sijainti aikoina s ja s; 2) keskinopeus näiden aikojen välillä kuluneelta ajalta; 3) hetkelliset nopeudet määrättyinä aikoina; 4) keskikiihtyvyys tietyltä ajanjaksolta; 5) hetkelliset kiihtyvyydet määritettyinä aikoina.
Kotitehtävä.
Harjoitella:
Etsi funktion differentiaali:
1. ![]() ;
;
2. ![]() ;
;
Etsi funktion toisen asteen derivaatat:
4. ![]()
5. ![]()
Etsi toisen asteen erot
6. ![]() .
.
7. Piste liikkuu lain mukaan suorassa linjassa. Laske nopeus ja kiihtyvyys ajoittain ja .
Etsi kasvavan ja pienenevän funktion välit:
9. ![]() .
.
10. Kun glukoosia infusoidaan, sen pitoisuus ihmisveressä, ilmaistuna asianmukaisina yksikköinä, jälkeen t tuntia tulee olemaan ![]() . Etsi verensokerin muutosnopeus kohteelle a) t = 1 h; b) t = 2 h.
. Etsi verensokerin muutosnopeus kohteelle a) t = 1 h; b) t = 2 h.
Teoria.
1. Luento aiheesta "Usean argumentin funktion derivaatit ja differentiaalit. Useiden argumenttien funktion differentiaalin soveltaminen.
2. Tämän oppaan oppitunti 3.
3. Pavlushkov I.V. ja muut s. 101-113, 118-121.
Oppitunti 3. Useiden argumenttien funktion derivaatat ja differentiaalit
Aiheen relevanssi: tätä matematiikan osaa käytetään laajalti useiden sovellettavien ongelmien ratkaisemisessa, koska monille fysikaalisen, biologisen, kemiallisen ilmiön ilmiöille on ominaista riippuvuus ei yhdestä, vaan useista muuttujista (tekijöistä).
Oppitunnin tarkoitus: oppia löytämään useiden muuttujien funktioiden osittaiset derivaatat ja differentiaalit.
Kohdetehtävät:
tietää: kahden muuttujan funktion käsite; kahden muuttujan funktion osittaisten derivaattojen käsite; useiden muuttujien funktion kokonais- ja osittaisten differentiaalien käsite;
osaa: löytää useiden muuttujien funktioiden derivaatat ja differentiaalit.
Lyhyt tieto teoreettiselta kurssilta
Peruskonseptit
Muuttujaa z kutsutaan kahden argumentin x ja y funktioksi, jos joillekin arvopareille on annettu tietty arvo z jonkin säännön tai lain mukaan. Kahden argumentin funktio on merkitty .
Funktio määritellään pintana suorakaiteen muotoisessa koordinaattijärjestelmässä avaruudessa. Kahden muuttujan funktion kuvaaja on pisteiden joukko kolmiulotteisessa avaruudessa x
Teos on ns yksityinen erotus funktiot z=f(x,y) by X ja ne on merkitty.
Funktion kokonaisdifferentiaali
Funktion differentiaali on tämän funktion osittaisten derivaattojen tulojen ja vastaavien riippumattomien muuttujien inkrementin summa, ts. ![]() . Koska
. Koska ![]() Ja
Ja ![]() sitten voit kirjoittaa:
tai
sitten voit kirjoittaa:
tai  .
.
Funktio on monimutkainen, jos se voidaan esittää funktion y = f[φ(x)] funktiona, missä y = f(u), au=φ(x), missä u on väliargumentti. Mikä tahansa monimutkainen funktio voidaan esittää perusfunktioina (yksinkertaisina), jotka ovat sen väliargumentteja.
Esimerkkejä:
Yksinkertaiset toiminnot: Monimutkaiset toiminnot:
y \u003d x 2 y \u003d (x + 1) 2; u \u003d (x + 1); y \u003d u 2;
y = sinx; y \u003d sin2x; u \u003d 2x; y = sinu;
y \u003d e x y \u003d e 2x; u \u003d 2x; y \u003d e u;
y \u003d lnx y \u003d ln (x + 2); u \u003d x + 2; y=lnu.
Yleinen sääntö monimutkaisen funktion erottamiseksi on annettu yllä olevalla lauseella ilman todistetta.
Jos funktiolla u \u003d φ (x) on derivaatta u "x \u003d φ" (x) pisteessä x ja funktiolla y \u003d f (u) on derivaatta y "u \u003d f " (u) vastaavassa pisteessä u, niin kompleksifunktion y \u003d f [φ (x)] derivaatta pisteestä x löytyy kaavasta: y "x \u003d f " (u) u "(x).
Tämän lauseen vähemmän tarkkaa mutta lyhyempää muotoilua käytetään usein. : kompleksisen funktion derivaatta on yhtä suuri kuin derivaatan tulo välimuuttujan suhteen ja välimuuttujan derivaatta riippumattoman muuttujan suhteen.
Esimerkki: y = sin2x2; u \u003d 2x 2; y = sinu;
y "x \u003d (sinu)" u (2x 2) "x \u003d cosu 4x \u003d 4x cos2x 2.
3. Toisen kertaluvun johdannainen. Toisen derivaatan mekaaninen merkitys.
Funktion y \u003d f (x) derivaatta kutsutaan ensimmäisen kertaluvun derivaataksi tai yksinkertaisesti funktion ensimmäiseksi derivaataksi. Tämä derivaatta on x:n funktio ja se voidaan erottaa toisen kerran. Derivaatan derivaatta kutsutaan toisen asteen derivaataksi tai toisen arvon derivaataksi. Se on merkitty: y "xx - (y kaksi vetoa päälle x); f "(x) – ( eff kaksi vetoa x:llä); d 2 y / dx 2 - (de kaksi y d x:llä kahdesti); d 2 f / dx 2 - (de kaksi ef d x:llä kahdesti).
Toisen derivaatan määritelmän perusteella voimme kirjoittaa:
y "xx \u003d (y" x) "x; f" (x) \u003d "x d 2 y / dx 2 \u003d d / dx (dy / dx).
Toinen derivaatta puolestaan on x:n funktio ja se voidaan erottaa kolmannen asteen derivaatan saamiseksi ja niin edelleen.
Esimerkki: y \u003d 2x 3 + x 2; y "xx \u003d [(2x 3 + x 2)" x] "x \u003d (6x 2 + 2x)" x \u003d 12x + 2;
Toisen derivaatan mekaaninen merkitys selitetään muuttuvaa liikettä luonnehtivan hetkellisen kiihtyvyyden perusteella.
Jos S=f(t) on liikeyhtälö, niin=S" t ; A vrt. =;
A inst. =  A cf =
A cf = 
 =" t ; A inst. = " t = (S" t)" t = S" tt .
=" t ; A inst. = " t = (S" t)" t = S" tt .
Siten reitin toinen derivaatta ajan suhteen on yhtä suuri kuin muuttuvan liikkeen hetkellinen kiihtyvyys. Tämä on 2. derivaatan fyysinen (mekaaninen) merkitys.
Esimerkki: Tapahtukoon materiaalipisteen suoraviivainen liike lain S=t 3 /3 mukaan. Aineellisen pisteen kiihtyvyys määritellään S "tt:n toisena derivaatana: A\u003d S "tt \u003d (t 3/3)" \u003d 2t.
4. Toimintoero.
Läheisesti derivaatan käsitteeseen liittyy funktion differentiaalin käsite, jolla on tärkeitä käytännön sovelluksia.
Funktio f( X) on johdannainen

 = f "
(X);
= f "
(X);
Lauseen mukaan (emme huomioi lausetta) äärettömän pienen suuren α(∆х)(  α(∆х)=0) derivaatalla:
α(∆х)=0) derivaatalla:  = f "
(х)+ α (∆х), mistä ∆f = f "
(х) ∆х+α(∆х) ∆х.
= f "
(х)+ α (∆х), mistä ∆f = f "
(х) ∆х+α(∆х) ∆х.
Viimeisestä yhtälöstä seuraa, että funktion inkrementti koostuu summasta, jonka jokainen termi on äärettömän pieni arvo kuten ∆х→ 0.
Määritetään tämän summan jokaisen äärettömän pienen arvon pienuus suhteessa äärettömän pieneen ∆х:

Siksi infinitesimaali f (х) ∆х ja ∆x ovat samaa suuruusluokkaa.

Siksi äärettömän pienellä arvolla α(∆х)∆х on suurempi pienuusaste verrattuna äärettömään pieneen arvoon ∆х. Tämä tarkoittaa, että ∆f:n lausekkeissa toinen termi α(∆х)∆х pyrkii 0:aan nopeammin kuin ∆х→0 kuin ensimmäinen termi f " (x)∆x.
Tämä on ensimmäinen termi f " (x)∆x kutsutaan funktion differentiaaliksi pisteessä x. Se on merkitty dy (de y) tai df (de ef). Joten dy=df= f " (x)∆x tai dy= f " (x)dx, koska argumentin differentiaali dx on yhtä suuri kuin sen inkrementti ∆x (jos kaavassa df= f " (x)dx hyväksy, että f(x)=x, niin saadaan df=dx=x"x ∆x, butx"x =1, eli dx=∆x). Joten funktion differentiaali on yhtä suuri kuin tämän funktion ja argumentin differentiaalin tulo.
Differentiaalin analyyttinen merkitys on siinä, että funktion differentiaali on pääosa funktion ∆f inkrementistä, lineaarinen argumentin ∆x suhteen. Funktion differentiaali eroaa funktion inkrementistä äärettömän pienellä arvolla α(∆х)∆х suurempi pienuusaste kuin ∆х. Todellakin ∆f=f " (х)∆х+α(∆х)∆х tai ∆f=df+α(∆х)∆х; mistä df= ∆f- α(∆х)∆х.
Esimerkki: y \u003d 2x 3 + x 2; dy \u003d? dy \u003d y "dx \u003d (2x 3 + x 2)" x dx \u003d (6x 2 + 2x) dx.
Jättäen huomioimatta korkeamman kertaluvun äärettömän pienen arvon α(∆x)∆x pienuus kuin ∆X, saamme df≈∆f≈ f " (x)dx eli funktion differentiaalia voidaan käyttää approksimoimaan funktion inkrementtiä, koska differentiaali on yleensä helpompi laskea. Differentiaalia voidaan soveltaa myös funktion arvon likimääräiseen laskemiseen. Tunnetaan funktio y= f(x) ja sen derivaatta pisteessä x. On tarpeen löytää funktion f(x+∆x) arvo jostain lähipisteestä (x+∆x). Tätä varten käytämme likimääräistä yhtälöä ∆у ≈dy tai ∆у ≈f " (x) ∆x. Kun otetaan huomioon, että ∆y=f(x+∆x)-f(x), saadaan f(x+∆x)-f (x) ≈f " (x) dx , mistä f(х+∆х) = f(х)+f " (x) dx. Tuloksena oleva kaava ratkaisee ongelman.
Johdannainen(funktiot pisteessä) - differentiaalilaskennan peruskäsite, joka kuvaa funktion muutosnopeutta (tietyssä pisteessä). Se määritellään rajaksi funktion lisäyksen suhteelle sen argumentin kasvuun, koska argumentin lisäys pyrkii nollaan, jos tällainen raja on olemassa. Funktiota, jolla on äärellinen derivaatta (jossain vaiheessa), kutsutaan differentioituvaksi (tietyssä pisteessä).
Johdannainen. Harkitse jotain toimintoa y = f (x ) kahdessa kohdassa x 0 ja x 0 + : f (x 0) ja f (x 0+). Tässä, jota tarkoittaa pieni muutos argumentissa, kutsutaan argumentin lisäys; vastaavasti funktion kahden arvon välinen ero: f (x 0 + ) f (x 0 ) kutsutaan funktion lisäys.johdannainen toimintoja y = f (x ) pisteessä x 0 jota kutsutaan rajaksi:


Jos tämä raja on olemassa, niin funktio f (x ) kutsutaan erottuva pisteessä x 0 . Funktiojohdannainen f (x ) on merkitty seuraavasti:


Derivaatan geometrinen merkitys. Tarkastellaan funktion kuvaajaa y = f (x ):


Kuvasta 1 voidaan nähdä, että funktion kaavion kahdelle pisteelle A ja B:


missä on sekantin AB kaltevuuskulma.
Siten erosuhde on yhtä suuri kuin sekantin kaltevuus. Jos kiinnitämme pisteen A ja siirrämme pistettä B sitä kohti, niin se pienenee loputtomasti ja lähestyy arvoa 0, ja sekantti AB lähestyy tangenttia AC. Siksi erosuhteen raja on yhtä suuri kuin tangentin kaltevuus pisteessä A. Tästä seuraa: funktion derivaatta pisteessä on kyseisen funktion kaavion tangentin kulmakerroin kyseisessä pisteessä. Tästä se koostuu geometrinen merkitys johdannainen.
Tangenttiyhtälö. Johdetaan funktion kaavion tangentin yhtälö pisteessä A ( x 0 , f (x 0 )). Yleisessä tapauksessa yhtälö suorasta kulmasta f ’(x 0 ) näyttää:
y = f ’(x 0 ) · x + b .
Löytää b, käytämme sitä tosiasiaa, että tangentti kulkee pisteen A kautta:
f (x 0 ) = f ’(x 0 ) · x 0 +b ,
täältä b = f (x 0 ) – f ’(x 0 ) · x 0 , ja korvaamalla tämän lausekkeen sanalla b, me tulemme saamaan tangenttiyhtälö:
y =f (x 0 ) + f ’(x 0 ) · ( x-x 0 ) .
Johdannan mekaaninen merkitys. Tarkastellaan yksinkertaisinta tapausta: materiaalin pisteen liike koordinaattiakselia pitkin ja liikkeen laki annetaan: koordinaatti x liikkuva piste on tunnettu funktio x (t) aika t. Aikavälillä alkaen t 0 - t 0 + piste siirtyy etäisyyden verran: x (t 0 + ) x (t 0) = , ja sen keskinopeus on yhtä suuri kuin: v a = . Nollassa keskinopeuden arvo pyrkii tiettyyn arvoon, jota kutsutaan välitön nopeus v ( t 0 ) olennainen ajankohta t 0 . Mutta johdannaisen määritelmän mukaan meillä on:


täältä v (t 0 ) = x' (t 0 ), ts. nopeus on koordinaatin derivaatta Tekijä: aika. Tästä se koostuu mekaaninen aisti johdannainen . Samoin kiihtyvyys on nopeuden derivaatta ajan suhteen: a = v' (t).
8. Taulukko johdannaisista ja differentiointisäännöistä


Puhuimme siitä, mikä johdannainen on artikkelissa "Dideriaatan geometrinen merkitys". Jos funktio on annettu kuvaajan avulla, sen derivaatta kussakin pisteessä on yhtä suuri kuin funktion kaavion tangentin kulmakertoimen tangentti. Ja jos funktio annetaan kaavalla, niin derivaattataulukko ja differentiaatiosäännöt auttavat sinua, eli säännöt derivaatan löytämiseksi.
§ 2. Johdannaisen määritelmä.
Anna toiminnon y=
f(x)
määritelty aikavälillä ( a;b). Mieti argumentin arvoa 
 (a;b)
. Lisätään argumenttia ∆
x
(a;b)
. Lisätään argumenttia ∆
x 
 0 niin, että ehto ( x 0
+∆
x)
0 niin, että ehto ( x 0
+∆
x)

 a;b). Merkitään funktion vastaavat arvot y 0:n ja y 1:n kautta:
a;b). Merkitään funktion vastaavat arvot y 0:n ja y 1:n kautta:
y 0 = f(x 0 ), y 1 = f(x 0 +∆ x). Siirtyessään pois x 0 Vastaanottaja x 0 +∆ x toimintoa kasvatetaan
∆y= y 1 -y 0 = f(x 0 +∆ x) -f(x 0 ). Jos, pyrkiessään ∆ x nollaan on raja funktion inkrementin suhteelle ∆y argumentin lisäykseen, joka kutsui sitä ∆ x,
nuo. on raja



 =
= 
 ,
,
silloin tätä rajaa kutsutaan funktion derivaatiksi y=
f(x)
pisteessä x 0
. Siis funktion derivaatta y=
f(x)
pisteessä x=x 0
funktion lisäyksen suhteelle argumentin kasvuun on raja, kun argumentin lisäys pyrkii nollaan. Funktiojohdannainen y=
f(x)
pisteessä x merkitty symboleilla 
 (x) tai
(x) tai 
 (x). Myös nimityksiä käytetään
,
(x). Myös nimityksiä käytetään
,


 ,
,
 ,
,
 . Kolme viimeistä merkintää korostaa sitä tosiasiaa, että derivaatta otetaan suhteessa muuttujaan x.
. Kolme viimeistä merkintää korostaa sitä tosiasiaa, että derivaatta otetaan suhteessa muuttujaan x.
Jos toiminto y= f(x) jolla on derivaatta jonkin intervallin jokaisessa pisteessä, sitten tällä välillä derivaatta ( x) on argumenttifunktio x.
§ 3. Johdannan mekaaninen ja geometrinen merkitys.
Funktiokaavion normaalin ja tangentin yhtälöt.
Kuten §:ssä 1 näkyy, pisteen hetkellinen nopeus on
v
=


 .
.
Mutta tämä tarkoittaa, että nopeus v on kuljetun matkan johdannainen S ajan kanssa t ,
v
=
 . Jos siis funktio y=
f(x)
kuvaa materiaalin pisteen suoraviivaisen liikkeen lakia, jossa y on materiaalin pisteen kulkema polku liikkeen alkamishetkestä ajan hetkeen x, sitten johdannainen ( x) määrittää pisteen hetkellisen nopeuden kerrallaan x. Tämä on johdannaisen mekaaninen merkitys.
. Jos siis funktio y=
f(x)
kuvaa materiaalin pisteen suoraviivaisen liikkeen lakia, jossa y on materiaalin pisteen kulkema polku liikkeen alkamishetkestä ajan hetkeen x, sitten johdannainen ( x) määrittää pisteen hetkellisen nopeuden kerrallaan x. Tämä on johdannaisen mekaaninen merkitys.
Kohdasta 1 löytyi myös funktion kuvaajan tangentin kaltevuus y= f(x) k= tgα= . Tämä relaatio tarkoittaa, että tangentin kaltevuus on yhtä suuri kuin derivaatta ( x). Tarkemmin sanottuna johdannainen ( x) toiminnot y= f(x) , lasketaan argumentin arvolla, joka on yhtä suuri kuin x, on yhtä suuri kuin tämän funktion kaavion tangentin kaltevuus pisteessä, jonka abskissa on yhtä suuri x. Tämä on derivaatan geometrinen merkitys.
Anna klo x=x 0 toiminto y= f(x) ottaa arvon y 0 =f(x 0 ) , ja tämän funktion kuvaajalla on tangentti pisteessä, jossa on koordinaatit ( x 0 ;y 0). Sitten tangentin kaltevuus
k = ( x 0). Käyttämällä yhtälöä tietyn pisteen kautta kulkeva suora viiva tiettyyn suuntaan, joka tunnetaan analyyttisen geometrian kurssista ( y-y 0 =k(x-x 0)), kirjoitamme tangenttiyhtälön:
Suoraa, joka kulkee kosketuspisteen kautta kohtisuorassa tangenttia vastaan, kutsutaan käyrän normaaliksi. Koska normaali on kohtisuorassa tangenttia vastaan, sen kaltevuus k normit liittyvät tangentin jyrkkyyteen k analyyttisestä geometriasta tunnettu relaatio: k normit = ─ ts. normaalille, joka kulkee pisteen läpi, jolla on koordinaatit ( x 0 ;y 0),k normi = ─ . Siksi tämän normaalin yhtälö on:

 (edellyttäen että
(edellyttäen että 
 ).
).
§ 4. Esimerkkejä johdannaisen laskemisesta.
Laskeaksesi funktion derivaatan y= f(x) pisteessä x, tarpeen:
Perustelu x lisäys ∆ x;
Etsi funktion ∆ vastaava inkrementti y=f(x+∆x) -f(x);
Luo suhde ;
Etsi tämän suhteen raja ∆:lle x→0.
Esimerkki 4.1. Etsi funktion derivaatta y=C=vakio.
Perustelu x anna lisäys ∆ x.
Aivan sama x, ∆y=0: ∆y=f(x+∆x) ─f(x)=С─С=0;
Täältä =0 ja =0, ts. =0.
Esimerkki 4.2. Etsi funktion derivaatta y=x.
∆ y=f(x+∆x) ─f(x)= x+∆x– x=∆ x;
1, =1, ts. =1.
Esimerkki 4.3. Etsi funktion derivaatta y=x 2.
∆ y= (x+∆ x)2–x 2= 2 x∙∆ x+ (∆ x)2;

 = 2 x+ ∆ x,
= 2 x, eli =2 x.
= 2 x+ ∆ x,
= 2 x, eli =2 x.
Esimerkki 4.4. Etsi funktion y=sin derivaatta x.
∆ y=sin( x+∆x) -synti x= 2 syntiä 
 cos( x+);
cos( x+);
= 
 ;
;
=


 = cos x, eli = cos x.
= cos x, eli = cos x.
Esimerkki 4.5. Etsi funktion derivaatta y=
 .
.
=
 , eli =
, eli = 
 .
.
JOHDANNAISEN MEKAANINEN MERKITYS
Fysiikasta tiedetään, että tasaisen liikkeen lailla on muoto s = v t, Missä s- polku kulki ajankohtaan asti t, v on tasaisen liikkeen nopeus.
Kuitenkin, koska suurin osa luonnossa tapahtuvista liikkeistä on epätasaisia, sitten yleensä nopeus ja siten etäisyys s riippuu ajasta t, eli tulee olemaan ajan funktio.
Annetaan siis materiaalipisteen liikkua suoraan yhteen suuntaan lain mukaan s=s(t).
Huomaa hetki aikaa t 0 . Tähän mennessä piste on ohittanut polun s=s(t 0 ). Määritetään nopeus v aineellinen hetki t 0 .
Voit tehdä tämän harkitsemalla jotakin muuta hetkeä t 0 + Δ t. Se vastaa kuljettua matkaa s =s(t 0 + Δ t). Sitten aikavälille Δ t piste on kulkenut polun Δs =s(t 0 + Δ t)–s(t).
Mietitään suhdetta. Sitä kutsutaan keskinopeudeksi aikavälillä Δ t. Keskinopeus ei pysty kuvaamaan tarkasti pisteen liikkeen nopeutta tällä hetkellä t 0 (koska liike on epätasainen). Jotta tämä todellinen nopeus voidaan ilmaista tarkemmin keskinopeudella, sinun on otettava pienempi aikaväli Δ t.
Eli liikkeen nopeus tiettynä ajankohtana t 0 (hetkellinen nopeus) on keskinopeuden raja aikavälillä alkaen t 0 - t 0 +Δ t kun Δ t→0:
![]()
![]() ,
,
nuo. epätasaisen liikkeen nopeus on kuljetun matkan johdannainen ajan suhteen.

 JOHDANNAISEN GEOMETRIINEN MERKITYS
JOHDANNAISEN GEOMETRIINEN MERKITYS
Otetaan ensin käyttöön käyrän tangentin määritelmä tietyssä pisteessä.
Olkoon meillä käyrä ja kiinteä piste siinä M 0(katso kuva) Harkitse toista kohtaa M tämä käyrä ja piirrä sekantti M 0 M. Jos kohta M alkaa liikkua käyrää ja pistettä pitkin M 0 pysyy paikallaan, sekantti muuttaa asentoaan. Jos, pisteen rajoittamattomalla approksimaatiolla M käyrästä pisteeseen M 0 millä tahansa puolella sekantti pyrkii ottamaan tietyn suoran paikan M 0 T, sitten suora viiva M 0 T kutsutaan käyrän tangentiksi annetussa pisteessä M 0.
Että., tangentti käyrään tietyssä pisteessä M 0 kutsutaan sekantin raja-asemaksi M 0 M kun piste M suuntautuu käyrää pitkin pisteeseen M 0.

 Harkitse nyt jatkuvaa funktiota y=f(x) ja tätä funktiota vastaava käyrä. Jotain arvoa vastaan X 0-funktio ottaa arvon y0=f(x0). Nämä arvot x 0 ja y 0 käyrällä vastaa pistettä M 0 (x 0; y 0). Esitetään argumentti x0 lisäys Δ X. Argumentin uusi arvo vastaa funktion lisättyä arvoa y 0 +Δ y=f(x 0 –Δ x). Saamme pisteen M(x 0+Δ x; v 0+Δ y). Piirretään sekantti M 0 M ja merkitään φ:llä sekantin muodostama kulma akselin positiivisen suunnan kanssa Härkä. Tehdään suhde ja huomioidaan se.
Harkitse nyt jatkuvaa funktiota y=f(x) ja tätä funktiota vastaava käyrä. Jotain arvoa vastaan X 0-funktio ottaa arvon y0=f(x0). Nämä arvot x 0 ja y 0 käyrällä vastaa pistettä M 0 (x 0; y 0). Esitetään argumentti x0 lisäys Δ X. Argumentin uusi arvo vastaa funktion lisättyä arvoa y 0 +Δ y=f(x 0 –Δ x). Saamme pisteen M(x 0+Δ x; v 0+Δ y). Piirretään sekantti M 0 M ja merkitään φ:llä sekantin muodostama kulma akselin positiivisen suunnan kanssa Härkä. Tehdään suhde ja huomioidaan se.
Jos nyt Δ x→0, funktion Δ jatkuvuudesta johtuen klo→0, ja siksi piste M, liikkuu käyrää pitkin, lähestyy loputtomasti pistettä M 0. Sitten sekantti M 0 M on taipumus ottaa käyrän tangentin asema pisteessä M 0, ja kulma φ→α kohdassa Δ x→0, jossa α tarkoittaa tangentin ja akselin positiivisen suunnan välistä kulmaa Härkä. Koska funktio tg φ riippuu jatkuvasti φ:stä kohdassa φ≠π/2, niin kohdassa φ→α tg φ → tg α ja siten tangentin kaltevuus on:
nuo. f"(x)= tgα.
Geometrisesti siis y "(x 0) edustaa tämän funktion kaavion tangentin jyrkkyyttä pisteessä x0, eli argumentin tietylle arvolle x, derivaatta on yhtä suuri kuin funktion kaavion tangentin muodostaman kulman tangentti f(x) vastaavassa kohdassa M 0 (x; y) positiivisella akselisuunnalla Härkä.
Esimerkki. Etsi käyrän tangentin kaltevuus y = x 2 kohdassa M(-1; 1).
Olemme jo nähneet sen ( x 2)" = 2X. Mutta käyrän tangentin kaltevuus on tg α = y"| x=-1 = -2.
Johdannan geometrinen, mekaaninen, taloudellinen merkitys
Johdannan määritelmä.
Luento №7-8
Bibliografia
1 Ukhobotov, V. I. Matematiikka: Oppikirja. - Tšeljabinsk: Tšeljab. osavaltio un-t, 2006.- 251 s.
2 Ermakov, V.I. Kokoelma korkeamman matematiikan tehtäviä. Opetusohjelma. -M.: INFRA-M, 2006. - 575 s.
3 Ermakov, V.I. Yleinen korkeamman matematiikan kurssi. Oppikirja. -M.: INFRA-M, 2003. - 656 s.
Teema "Johdannainen"
Kohde: Selitä derivaatan käsite, jäljitä funktion jatkuvuuden ja differentiatiivisuuden suhde, näytä derivaatan käytön soveltuvuus esimerkein.
.Tätä taloustieteen rajaa kutsutaan tuotannon rajakustannuksiksi.
Johdannan määritelmä. Derivaatan geometrinen ja mekaaninen merkitys, kuvaajaa tangentin funktion yhtälö.
Tarvitsetko lyhyen vastauksen (ei ylimääräistä vettä)
Kuollut_valkoinen_lumi
Derivaata on differentiaalilaskennan peruskäsite, joka kuvaa funktion muutosnopeutta.
Geometrinen?
Toiminnan tangentti pisteessä... .
Toiminnan lisäysehto: f "(x) > 0.
Pienevä funktion ehto: f "(x)< 0.
Käännepiste (tarvittava ehto): f " " (x0) = 0.
Kupera ylös: f " " (x) Kupera alas: f " " (x) >0
Normaali yhtälö: y=f(x0)-(1/f `(x0))(x-x0)
Mekaaninen?
Nopeus on derivaatta etäisyyden suhteen, kiihtyvyys on derivaatta nopeuden suhteen ja toinen derivaatta etäisyyden suhteen...
Funktion f kuvaajan tangentin yhtälö pisteessä x0
y=f(x0)+f `(x0)(x-x0)
Käyttäjä poistettu
Jos funktion delta y inkrementin delta y ja sen aiheuttaneen argumentin delta x lisäyksen suhteelle delta y on raja, kun delta x pyrkii nollaan, niin tätä rajaa kutsutaan funktion derivaatiksi. y = f (x) tietyssä pisteessä x ja sitä merkitään y "tai f" (x)
Suoraviivaisen liikkeen nopeus v on reitin s derivaatta ajan t suhteen: v = ds/dt. Tämä on johdannaisen mekaaninen merkitys.
Käyrän y \u003d f (x) tangentin kaltevuus pisteessä, jossa on abskissa x nolla, on f "(x nolla) derivaatta. Tämä on derivaatan geometrinen merkitys.
Tangenttikäyrää pisteessä M nolla kutsutaan suoraksi M nolla T, jonka kaltevuus on yhtä suuri kuin sekantin M nolla M yksi kaltevuuden raja, kun delta x pyrkii nollaan.
tg phi = lim tg alfa kun delta x lähestyy nollaa = lim (delta x/delta y) kun delta x lähestyy nollaa
Derivaatan geometrisesta merkityksestä tangenttiyhtälö saa muodon:
y - y nolla = f "(x nolla) (x - x nolla)
Ohjekortti nro 20
Takyryby/Aihe: « Toinen derivaatta ja sen fyysinen merkitys ».
Maқsaty / Tarkoitus:
Osaa löytää tangentin yhtälön sekä tangentin kaltevuuskulman tangentin OX-akseliin nähden. Osaa löytää funktion muutosnopeuden sekä kiihtyvyyden.
Luo edellytys taitojen muodostumiselle vertailla, luokitella tutkittuja tosiasioita ja käsitteitä.
Kasvatetaan vastuullista asennetta kasvatustyöhön, tahtoa ja sinnikkyyttä saavuttaa lopputuloksia tangenttiyhtälön sekä toiminnan muutosnopeuden ja kiihtyvyyden selvittämisessä.
Teoreettinen materiaali:
(Johdannan geometrinen merkitys)
Funktiokaavion tangentin yhtälö on:
Esimerkki 1: Etsitään funktion kaavion tangentin yhtälö pisteestä, jossa on obskissa 2.
Vastaus: y = 4x-7
Funktion kuvaajan tangentin kulmakerroin k pisteessä, jossa on abskissa x o, on yhtä suuri kuin f / (x o) (k = f / (x o)). Funktion kuvaajan tangentin kaltevuuskulma tietyssä pisteessä on
arctg k \u003d arctg f / (x o), ts. k = f/(x o) = tg
Esimerkki 2:
Missä kulmassa sinusoidi on ![]() leikkaa x-akselin origossa?
leikkaa x-akselin origossa?
Kulma, jossa tämän funktion kuvaaja leikkaa abskissa-akselin, on sama kuin funktion f (x) kuvaajaan tässä pisteessä piirretyn tangentin kaltevuuskulma a. Etsitään derivaatta: Ottaen huomioon derivaatan geometrisen merkityksen, meillä on: ja a = 60°. Vastaus: =60 0 .
Jos funktiolla on johdannainen jokaisessa pisteessä sen toimialueella, niin sen derivaatta on funktio . Funktiolla voi puolestaan olla derivaatta, jota kutsutaan toisen asteen johdannainen toiminnot (tai toinen johdannainen) ja ne on merkitty symbolilla .
Esimerkki 3: Etsi funktion toinen derivaatta: f(x)=x 3 -4x 2 +2x-7.
Alussa löydämme tämän funktion ensimmäisen derivaatan f "(x) \u003d (x 3 -4x 2 + 2x-7) '= 3x 2 -8x + 2,
Sitten löydämme saadun ensimmäisen derivaatan toisen derivaatan
f""x)=(3x2 -8x+2)''=6x-8. Vastaus: f""x) = 6x-8.
(Toisen derivaatan mekaaninen merkitys)
Jos piste liikkuu suorassa ja sen liikkeen laki on annettu, niin pisteen kiihtyvyys on yhtä suuri kuin reitin toinen derivaatta ajan suhteen:
Materiaalikappaleen nopeus on yhtä suuri kuin polun ensimmäinen derivaatta, eli:
Materiaalikappaleen kiihtyvyys on yhtä suuri kuin nopeuden ensimmäinen derivaatta, eli:
Esimerkki 4:
Keho liikkuu suorassa linjassa lain s (t) \u003d 3 + 2t + t 2 (m) mukaan. Määritä sen nopeus ja kiihtyvyys hetkellä t = 3 s. (Reitti mitataan metreissä, aika sekunneissa).
Ratkaisu
v (t) = s΄ (t) =(3+2t+t 2)'= 2 + 2t
a (t) = v΄ (t) =(2+2t)'= 2 (m/s 2)
v(3) = 2 + 2-3 = 8 (m/s). Vastaus: 8 m/s; 2 m/s2.
Käytännön osa:
| 1 vaihtoehto | Vaihtoehto 2 | 3 vaihtoehto | 4 vaihtoehto | 5 vaihtoehto |
| Etsi annetun pisteen M kautta kulkevan tangentin x-akselin kaltevuuskulman tangentti funktion f kuvaaja. |
||||
| f(x)=x2, M(-3;9) | f(x)=x3, M(-1;-1) | |||
| Kirjoita funktion f kuvaajan tangentin yhtälö pisteessä, jonka abskissa on x 0. |
||||
| f (x) \u003d x 3 -1, x 0 \u003d 2 | f (x) \u003d x 2 +1, x 0 \u003d 1 | f (x) \u003d 2x-x 2, x 0 \u003d -1 | f(x) = 3sinx, x 0 = | f(x) = x 0 = -1 |
| Etsi funktion f tangentin kaltevuus pisteessä, jonka abskissa on x 0. |
||||
| Etsi funktion toinen derivaatta: |
||||
| f(x) = 2cosx-x 2 | f(x)= -2sinx+x 3 |
|||
| Kappale liikkuu suorassa linjassa lain x (t) mukaan. Määritä sen nopeus ja kiihtyvyys tällä hetkellä aika t. (Siirtymä mitataan metreinä, aika sekunteina). |
||||
| x(t) = t2-3t, t = 4 | x(t) = t3 +2t, t = 1 | x(t) = 2t3-t2, t = 3 | x(t)=t3-2t2+1,t=2 | x (t) \u003d t 4 -0,5t 2 \u003d 2, t \u003d 0,5 |
Kontrollikysymykset:
Mikä on mielestäsi derivaatan fyysinen merkitys - onko se hetkellinen nopeus vai keskinopeus?
Mikä on yhteys funktion kuvaajaan minkä tahansa pisteen kautta piirretyn tangentin ja derivaatan käsitteen välillä?
Mikä on funktion kaavion tangentin määritelmä pisteessä M (x 0; f (x 0))?
Mikä on toisen derivaatan mekaaninen merkitys?