Признаци за сходимост на несобствени интеграли. Неправилни интеграли Определение и основни свойства

Теорема 12.11 (тест за сравнение на неправилни интеграли). Нека функциите f(x) и g(x) са непрекъснати в интервала [a, ">) и отговарят на условието 0 fix) ?(x) в него. Тогава от сходимостта на интеграла

следва сходимостта на интеграла

и обратно, разминаването на интеграла (12.64) предполага разминаване на интеграла (12.63).

Доказателство.Нека въведем обозначението:

функция P(K)е ненамаляващ; всъщност, ако и аз 2, тогава

Дж поправи) dx>0 и след това

Вземете последователността от стойности (/? „) -> “>; след това съответната последователност от функционални стойности (F(Rn))е монотонна и ненамаляваща. Нека интегралът (12.63) се сближи, тогава последователността (67 ( Рто)) е ограничено; но тогава последователността също е ограничена (Ф(/?n)) и следователно, по силата на теорема 7.13, тя се събира. Следователно има ограничение F(R)при Р-+ ">, т.е. интеграл (12.64) се събира.

Сега доказваме втората част на теоремата; нека интегралът (12.64) се разминава. Ако приемем, че интегралът (12.63) се сближава, то от доказаното по-горе интегралът (12.64) също трябва да се сближава, което противоречи на условието. Теоремата е доказана. ?

Коментирайте.Подобен критерий за сравнение е валиден и за неправилни интеграли от втори род. Ако функциите f(x) и ж (Х)непрекъснато на полуинтервала [a> b)и за всички точки в някаква околност на особената точка bизпълнени

условия 0 (x), тогава от сходимостта на интеграла Jg(x)dx следва, че

интеграла J/(x)dx, а от дивергенцията на интеграла J/(x)dx - дивергенцията

мост на интеграла Jg(x)dx.

Нека разгледаме примери за изследване на сходимостта на неправилни интеграли.

Пример 27. T . ^-.

X 3 (1 + e L)

Решение.Нека сравним подинтегралната функция в този интеграл с функцията

Dg. Очевидно е, че -g- -

х r* (1+0 x J

градът J-jdx се сближава; следователно, по силата на критерия за сравнение се сближава и 1 х

всеки интеграл.

Пример 28. I-.

Решение.Сравнявайки интегралната функция на този интеграл с функцията 1/x,

виждаме, че (1 + In x)/x > 1/x на интервал 1

се разминава, следователно даденият интеграл се разминава и по критерия за сравнение.

В заключение представяме без доказателство критерия на Коши за сходимост на неправилен интеграл от първи род.

12.10.4. Абсолютна и условна сходимост на несобствени интеграли

Определение 5. Извиква се неправилен интеграл J/(x)dx абсолютно

сближаване, ако интегралът J|/(x)|dx се сближава.

Определение 6. Несобственият интеграл J /(x) dx се нарича условно подобни

тлеещ, ако конвергира и интегралът J|/(x)|dx се разминава.

Забележете, че абсолютната сходимост на интеграла предполага неговата сходимост по силата на оценка 3 на определения интеграл и критерия на Коши.

Теорема 12.13 (тест на Дирихле-Абел*). Нека функцията f(x) е непрекъсната и има ограничена първоизводна Е(x) на интервала [a, ">), докато функцията g(x) има непрекъсната производна на този интервал, не нараства и клони към нула като x -> ©o. Тогава неправилният интеграл

се сближава.

Доказателство.Прилагаме интегриране по части към интеграла J /(x)g(x)dx

на произволен сегмент R R"с [ А, °°). Ние имаме:

Теорема 12.12. За сходимостта на неправилния интеграл (12.64) е необходимо и достатъчно за всяко e > 0 да може да се намери такова число А> 0, което за всяко R"и /?", по-голям от а,важи следното неравенство:

Според теоремата F(x)ограничено, т.е. |F(x)| K. Функцията g(x) не нараства и клони към нула при х -» «>, следователно. g(x)> 0 и g"(x)

Абел Нилс Хенрик (1802-1829) Норвежки математик.

Тъй като, съгласно хипотезата на теоремата, g(x) -> 0 като x -> ©°, за произволно число e > 0 можете да намерите числото A>такъв, че при R"> Lнеравенството ще бъде изпълнено g(R") Замествайки това в оценка (12.68), получаваме:

което съответства на критерия на Коши за сходимост на интеграла (12.66). Теоремата е доказана. ?

Разгледайте примери за използване на теста на Дирихле-Абел за сходимост на неправилни интеграли.

Пример 29. f^^dx, a > 0.

Решение.Поставяме / (x) \u003d sin x, g(x)= l/x"; лесно е да се провери, че всички условия на теоремата са изпълнени, т.е. този интеграл се сближава. За a > 1 този интеграл

ral се сближава абсолютно. Наистина, |грях x/xP 1/d L, интеграл J(l/x e)dx

конвергира, т.е. за сравнение (теорема 12.11), този интеграл също се сближава абсолютно.

Пример 30. Jsin x 2 dx - интеграл на Френел, o

Решение.Ние представяме този интеграл като сума:

Тъй като sin x 2 е непрекъсната функция на сегмента (0, 1J), първият интеграл в (12.69) съществува. За да определим сходимостта на неправилния интеграл от дясната страна на (12.69), задаваме / (x) \ u003d x sin x 2, ж(x) = 1/x. Тогава за функцията f(x) първоизводната F(x) = -cosx 2 /!е ограничено в интервала |1, ">), докато #(x) е положителен, клони към нула при x -» °° и има непрекъсната производна върху (1, ©o). Следователно, съгласно критерия на Дирихле - Абел, вторият интеграл в (12.69) се събира, т.е. интегралът на Френел също се събира.

Неправилни интеграли от първи род.Всъщност това е един и същ определен интеграл, но в случаите, когато интегралите имат безкрайна горна или долна граница на интегриране, или и двете граници на интегриране са безкрайни.

Неправилни интеграли от втори род.Всъщност това е същият определен интеграл, но в случаите, когато интегралът е взет от неограничени функции, интеграндът няма интеграция в краен брой точки от крайния сегмент, обръщайки се към безкрайност.

За сравнение.При въвеждането на понятието определен интеграл се приемаше, че функцията f(х) е непрекъснат на отсечката [ а, b], а интервалът на интегриране е краен, т.е. ограничен е от числа, а не от безкрайност. Някои задачи водят до необходимостта от изоставяне на тези ограничения. Така се появяват неправилните интеграли.

Геометричният смисъл на неправилния интегралсе оказва доста просто. Когато графиката на функцията г = f(х) е над оста вол, определеният интеграл изразява площта криволинеен трапец, ограничена крива г = f(х) , абсциса и ординати х = а , х = b. На свой ред неправилният интеграл изразява площта на неограничен (безкраен) криволинеен трапец, затворен между линиите г = f(х) (на снимката по-долу в червено) х = аи абсцисната ос.

Неправилните интеграли се дефинират по подобен начин за други безкрайни интервали:

Площта на безкраен криволинеен трапец може да бъде крайно число и в този случай неправилният интеграл се нарича конвергентен. Площта може да бъде и безкрайност, в който случай неправилният интеграл се нарича дивергент.

Използване на границата на интеграл вместо самия неправилен интеграл.За да изчислите неправилния интеграл, трябва да използвате границата на определения интеграл. Ако тази граница съществува и е крайна (не е равна на безкрайност), тогава неправилният интеграл се нарича конвергентен, в противен случай той е дивергентен. Към какво клони променливата под граничния знак зависи от това дали имаме работа с неправилен интеграл от първи вид или от втори род. Нека разберем за това сега.

Несобствени интеграли от първи род – с безкрайни граници и тяхната сходимост

Неправилни интеграли с безкрайна горна граница

И така, записът на неправилния интеграл се различава от обичайния определен интеграл по това, че горната граница на интегриране е безкрайна.

Определение. Неправилен интеграл с безкрайна горна граница на интегриране от непрекъсната функция f(х) между а преди ∞ се нарича граница на интеграла на тази функция с горна граница на интегриране b и долната граница на интеграция а при условие, че горната граница на интеграция расте неограничено, т.е.

.

Ако тази граница съществува и е равна на някакво число, а не на безкрайност, тогава неправилният интеграл се нарича конвергентен, а числото, равно на границата, се приема за негова стойност. В противен случай неправилният интеграл се нарича дивергенти не му се приписва никаква стойност.

Пример 1. Изчисляване на неправилен интеграл(ако се сближава).

Решение. Въз основа на дефиницията на неправилния интеграл намираме

Тъй като границата съществува и е равна на 1, то даденото неправилен интеграл се събираи е равно на 1.

В следващия пример интегралната функция е почти същата като в пример 1, само степента на x не е две, а буквата алфа и задачата е да се изследва неправилният интеграл за сходимост. Тоест остава да се отговори на въпроса: при какви стойности на алфа този неправилен интеграл се сближава и при какви стойности се отклонява?

Пример 2. Изследване на сходимостта на неправилен интеграл(долната граница на интегриране е по-голяма от нула).

Решение. Да предположим първо, че , тогава

В получения израз преминаваме към границата при:

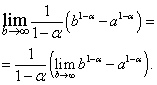
Лесно се вижда, че границата от дясната страна съществува и е равна на нула, когато , т.е., и не съществува, когато , т.е.

В първия случай, когато . Ако , тогава и не съществува.

Заключението от нашето проучване е следното: неправилен интеграл се събирапри и се разминавапри .

Прилагане към изследвания тип неправилен интеграл на формулата на Нютон-Лайбниц , можем да изведем следната много подобна формула:

.

Това е обобщената формула на Нютон-Лайбниц.

Пример 3. Изчисляване на неправилен интеграл(ако се сближава).

Границата на този интеграл съществува:

Вторият интеграл, който е сумата, изразяваща първоначалния интеграл:

Съществува и границата на този интеграл:

.

Намираме сумата от два интеграла, която също е стойността на първоначалния неправилен интеграл с две безкрайни граници:

Несобствени интеграли от втори род - от неограничени функции и тяхната сходимост

Нека функцията f(х) зададен на сегмента от а преди b и неограничено върху него. Да предположим, че функцията отива в безкрайност в точката b , докато във всички останали точки на отсечката е непрекъсната.

Определение. Неправилен интеграл на функцията f(х) на отсечката от а преди b се нарича граница на интеграла на тази функция с горна граница на интегриране ° С , ако при стремеж ° С Да се b функцията нараства неограничено, а в точката х = b функция не е дефинирана, т.е.

.

Ако тази граница съществува, тогава неправилният интеграл от втори род се нарича конвергентен, в противен случай дивергентен.

Използвайки формулата на Нютон-Лайбниц, извеждаме.

Примери за изследване на неправилни интеграли за сходимост

Пример 1
.

По този начин този интеграл се събира за a > 1 и се разминава за a £ 1.

Пример 2 Проучете за конвергенция. Изчисляваме интеграла по дефиниция:
.

По този начин този интеграл се събира за a<1 и расходится при a³1.

Пример 3 Проучете за конвергенция .

<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два

.

Изследваме сходимостта на първия интеграл I1, като използваме еквивалентна функция: (защото n>0) и интегралът се сближава, когато m>-1 (пример 2). По същия начин за интеграла I2:

И интегралът се събира за m+n<-1 (пример2). Следовательно, исходный интеграл сходится при выполнении одновременно двух условий m>-1 и m+n<-1, и будет расходится при нарушении хотя бы одного из них.

Пример 4 Проучете за конвергенция.

Интегрантът може да бъде безкрайно голям (ако m<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два:

Тъй като arctgx »x при x®0, тогава интегралът I1 е еквивалентен на интеграла , който се събира за m+1>-1, т.е. за m>-2 (пример 1).

За подинтегралната функция в неправилния интеграл от първи род I2 избираме еквивалентен:

тъй като arctgx » p/2 за x® ¥. Следователно, според втория критерий за сравнение, интегралът I2 ще се сближи за m + n<-1, и расходится в противном случае.

Комбинирайки условията за сходимост на интегралите I1 и I2, получаваме условията за сходимост на първоначалния интеграл: m>-2 и m+n<-1 одновременно.

Коментирайте.В примери 2-4 е използван критерий за сравнение 2, който осигурява необходимите и достатъчни условия за сближаване, което позволява чрез задаване на сближаване при определено условие на стойностите на параметрите да не се доказва разминаването на интеграла ако получените условия за конвергенция са нарушени.

Пример 5 Проучете за конвергенция.

Този интеграл съдържа особена точка 0, в която интеграндът може да стане безкраен за p<0, поэтому снова разобьем исходный интеграл на два:

.

Интегралът I1 е неправилен интеграл от втори вид и интеграндът е еквивалентен при x®0 на функцията xp (e-x ®1 при x®0), т.е. I1 се сближава за p>-1 (пример 1).

Интегралът I2 е неправилен интеграл от първи род. Изберете функция, еквивалентна на интегрант, така че да не съдържа експоненциална функция, се проваля. Следователно е невъзможно да се използва критерий за сравнение 2, както в предишните примери. Нека приложим първия критерий за сравнение, за който използваме следния добре известен факт:

За a>0 и всяко p. От това и факта, че функцията xpe-ax е непрекъсната, следва, че тази функция е ограничена, т.е. съществува константа M>0, такава че xpe-ax< M. Возьмем, например, a=1/2, и оценим интеграл I2 сверху:

Тоест, интегралът I2 се събира за всяко p.

Така първоначалният интеграл се сближава за p>-1.

Пример 6 Проучете за конвергенция.

Нека променим променливата: t = lnx и да получим

Разделянето на интеграла на две се извършва подобно на пример 5. Интегралът I1 е напълно еквивалентен на интеграла I1 от пример 5 и следователно се сближава за q<1.

Разгледайте интеграла I2. При спазване на 1-т<0 этот интеграл полностью эквивалентен интегралу I2 в примере 5 (доказательство сходимости аналогично, а условие 1-p<0 нужно для выполнения и a=(1-p)/2.).

И така, I2 се сближава за p>1. Това изследване на конвергенцията на този интеграл обаче не е завършено, тъй като използваният критерий за конвергенция дава само достатъчни условия за конвергенция. Следователно е необходимо изследване на конвергенцията като 1-p £ 0.

Да разгледаме случая p=1. Тогава интегралът I2 е еквивалентен на , който се сближава за q>1 (обърнете внимание, че интегралът I1 се разминава в този случай) и се разминава в противен случай.

За стр<1 оценим интеграл I2 и покажем его расходимость. Для этого вспомним, что За 1-p>0 и следователно, започвайки от някои A>1, T- Qд(1- П) T³M=const>0. Тогава интегралът I2 удовлетворява оценката

,

Където интегралът от дясната страна се разминава, което доказва разминаването на интеграла I2 .

Обобщавайки получените резултати, получаваме, че първоначалният интеграл се сближава за q<1 и p>1, в противен случай интегралът се разминава.

Пример 6 Проверете за абсолютна и условна конвергенция.

Нека разделим оригиналния интеграл на две:

.

Конвергенция.Интегралът I1 е еквивалентен на , т.е. се сближава за p<2 (пример 1) , причем абсолютно, так как подынтегральная функция положительна на отрезке интегрирования.

Интегралът I2 се сближава около критерия на Дирихле-Абел за p>0, тъй като първоизводната sin(x) е ограничена и функцията 1/xp клони монотонно към нула, когато x клони към безкрайност.

Нека покажем, че при p £ 0 интегралът се разминава. За това използваме критерия на Коши или по-скоро неговото отрицание

.

Нека вземем следните стойности като R1 и R2: R1=2pk и R2=2pk+p/2, тогава

, за p>0.

Така интегралът се събира при 0

Абсолютна конвергенцияАбсолютната конвергенция на интеграла I1 вече е установена, нека разгледаме абсолютната конвергенция на I2. Нека оценим интеграла отгоре:

, т.е. интегралът се събира за p>1.

За да докажем дивергенцията за p £ 1, оценяваме интеграла отдолу

.

Разделяме последния интеграл на разликата на функциите на разликата на интегралите

.

Ако и двата интеграла се сближават, тогава интегралът на разликата се сближава; ако единият от интегралите се разминава, а другият се сближава, тогава интегралът на разликата се разминава. В случай на разминаване на двата интеграла, сходимостта на интеграла на разликата подлежи на допълнително изследване. Нас ни интересува вторият от описаните случаи.

Дивергент (пример 1) на стр<1. сходится по признаку Дирихле-Абеля при 1>p>0 (виж Конвергенция), следователно интегралът се оценява отдолу чрез дивергентен интеграл, т.е. той се разминава.

Случаят p³1 не ни интересува, тъй като интегралът се разминава за тези стойности на параметъра.

По този начин първоначалният интеграл се събира абсолютно при 0

Ако подинтегралната функция има прекъсване от втори род на (крайния) интервал на интегриране, се говори за неправилен интеграл от втори род.

10.2.1 Определение и основни свойства

Нека обозначим интервала на интегриране $\left[ a, \, b \right ]$, и двете числа се приемат за крайни по-долу. Ако има само 1 пропуск, той може да бъде или в точката $a$, или в точката $b$, или вътре в интервала $(a,\,b)$. Нека първо разгледаме случая, когато в точка $a$ има прекъсване от втори род, а в останалите точки подинтегралната функция е непрекъсната. Така че обсъждаме интеграла

\begin(equation) I=\int _a^b f(x)\,dx, (22) \label(intr2) \end(equation)

където $f(x) \rightarrow \infty $, когато $x \rightarrow a+0$. Както и преди, първото нещо, което трябва да направите, е да придадете значение на този израз. За да направите това, помислете за интеграла

\[ I(\epsilon)=\int _(a+\epsilon)^b f(x)\,dx. \]

Определение. Нека има граница

\[ A=\lim _(\epsilon \rightarrow +0)I(\epsilon)=\lim _(\epsilon \rightarrow +0)\int _(a+\epsilon)^b f(x)\,dx. \]

Тогава се казва, че неправилният интеграл от втори вид (22) се сближава и му се приписва стойността $A$, а самата функция $f(x)$ се казва, че е интегрируема в интервала $\left[ a, \ , b\вдясно]$.

Нека разгледаме варианта, когато има прекъсване на втория род на подинтегралната функция на горната граница на интервала на интегриране. Този случай може да бъде намален до предишния чрез промяна на променливата $x=-t$ и след това пренареждане на границите на интегриране.

Нека разгледаме случая, когато подинтегралната функция има прекъсване от втори род вътре в интервала на интегриране, в точката $c \in (a,\,b)$. В този случай оригиналният интеграл

\begin(equation) I=\int _a^bf(x)\,dx (23) \label(intr3) \end(equation)

представени като сума

\[ I=I_1+I_2, \quad I_1=\int _a^cf(x)\,dx +\int _c^df(x)\,dx. \]

Определение. Ако и двата интеграла $I_1, \, I_2$ се събират, тогава неправилният интеграл (23) се нарича конвергентен и му се приписва стойност, равна на сумата от интегралите $I_1, \, I_2$, функцията $f(x) $ се нарича интегрируем в интервала $\left [a, \, b\right]$. Ако поне един от интегралите $I_1,\, I_2$ е дивергент, неправилният интеграл (23) се казва, че е дивергент.

Сходящите неправилни интеграли от 2-ри род имат всички стандартни свойства на обикновените определени интеграли.

1. Ако $f(x)$, $g(x)$ са интегрируеми на интервала $\left[ a, \,b \right ]$, тогава тяхната сума $f(x)+g(x)$ е също интегрируем в този интервал, и \[ \int _a^(b)\left(f(x)+g(x)\right)dx=\int _a^(b)f(x)dx+\int _a^( b)g (x)dx. \] 2. Ако $f(x)$ е интегрируем в интервала $\left[ a, \, b \right ]$, тогава за всяка константа $C$ функцията $C\cdot f(x)$ също е интегрируем на този интервал и \[ \int _a^(b)C\cdot f(x)dx=C \cdot \int _a^(b)f(x)dx. \] 3. Ако $f(x)$ е интегрируем в интервала $\left[ a, \, b \right ]$ и $f(x)>0$ в този интервал, тогава \[ \int _a^( б) f(x)dx\,>\,0. \] 4. Ако $f(x)$ е интегрируемо в интервала $\left[ a, \, b \right ]$, тогава за всяко $c\in (a, \,b)$ интегралите \[ \ int _a^ (c) f(x)dx, \quad \int _c^(b) f(x)dx \] също се събират и \[ \int _a^(b)f(x)dx=\int _a ^(c ) f(x)dx+\int _c^(b) f(x)dx \] (адитивност на интеграла върху интервала).

Разгледайте интеграла

\begin(equation) I=\int _0^(1)\frac(1)(x^k)\,dx. (24) \label(mod2) \end(уравнение)

Ако $k>0$, интегралът клони към $\infty$ като $x \rightarrow +0$, така че интегралът е неправилен от втори вид. Представяме ви функцията

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx. \]

В този случай антипроизводното е известно, така че

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k )|_(\epsilon)^1= \frac(1)(1-k)-\frac(\epsilon ^(1-k))(1-k). \]

за $k \neq 1$,

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x)\,dx\,=lnx|_(\epsilon)^1= -ln \epsilon. \]

за $k = 1$. Като се има предвид поведението за $\epsilon \rightarrow +0$, заключаваме, че интегралът (20) се сближава за $k

10.2.2 Критерии за сходимост на неправилни интеграли от 2-ри род

Теорема (първият знак за сравнение). Нека $f(x)$, $g(x)$ са непрекъснати за $x\in (a,\,b)$ и $0 1. Ако интегралът \[ \int _a^(b)g(x) dx \] се сближава, тогава интегралът \[ \int _a^(b)f(x)dx също се сближава. \] 2. Ако интегралът \[ \int _a^(b)f(x)dx \] се разминава, тогава интегралът \[ \int _a^(b)g(x)dx също се разминава. \]

Теорема (вторият знак за сравнение). Нека $f(x)$, $g(x)$ са непрекъснати и положителни за $x\in (a,\,b)$ и нека има крайна граница

\[ \theta = \lim_(x \rightarrow a+0) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \]

След това интегралите

\[ \int _a^(b)f(x)dx, \quad \int _a^(b)g(x)dx \]

се сближават или разминават едновременно.

1. Неправилни интеграли с безкрайни граници

Спомнете си дефиницията на интеграл като граница на интегралните суми:

Дефиницията предполага, че интервалът на интегриране е краен и функцията f (x) е непрекъсната в него. Нарушаването на тези предположения води до неправилни интеграли.

Определение.Ако интегралът клони към краен предел с неограничено нарастване "б", тогава тази граница се нарича неправилен интеграл с безкрайна горна граница на функцията f (x) и се обозначава със символа

В този случай се казва, че неправилният интеграл съществува или се сближава.

Ако определената граница не съществува или съществува, но е безкрайна, тогава се казва, че интегралът не съществува или се разминава.

Неправилният интеграл с безкрайна долна граница се дефинира по подобен начин:

Неправилен интеграл с две безкрайни граници се определя от формулата:

където c е всяка фиксирана точка на оста x.

И така, неправилните интеграли могат да бъдат с безкрайно долна граница, с безкрайно горна граница, а също и с две безкрайни граници.

Признаци на конвергенция. Абсолютна и условна конвергенция

Интегралът съществува само когато всеки от интегралите съществува: и .

Пример.Изследвайте сходимостта на интеграла

Ако приемем c = 0, получаваме:

тези. интегралът се събира.

Понякога не е необходимо да се изчислява неправилният интеграл, а е достатъчно да се знае дали той се сближава или се разминава, като се сравни с друг интеграл.

Теорема за сравнение за неправилни интеграли.

Нека функцията f (x) има няколко (краен брой) точки на прекъсване от първи вид в интервала, това „препятствие“ може лесно да бъде елиминирано чрез разделяне на сегмента с точки на прекъсване на няколко сегмента, изчисляване на определените интеграли на всеки отделен участък и добавете резултатите.

Обмисли определен интегралот функция, която е неограничена при приближаване до един от краищата на сегмента, например, .

(В такива случаи обикновено се казва: „Функцията има безкрайно прекъсване в десния край на интеграционния сегмент.“)

Ясно е, че обичайната дефиниция на интеграла тук губи значението си.

Определение. Неправилният интеграл на функцията f(x), който е непрекъснат за a £ x< b и неограниченной при x ® b - 0, называется предел:

По подобен начин се дефинира неправилният интеграл на функция, която има безкрайно прекъсване в левия край на сегмента:

Следователно в областта [ -1, 0] интегралът се разминава.

Това означава, че интегралът също се разминава на отсечката.

По този начин този интеграл се разминава на целия сегмент [-1, 1]. Обърнете внимание, че ако започнем да изчисляваме този интеграл, без да обръщаме внимание на прекъсването на интегралната функция в точката x = 0, ще получим неправилен резултат. Наистина ли,

, което е невъзможно.

Така че, за да изследваме неправилния интеграл на прекъсната функция, е необходимо да го "разбием" на няколко интеграла и да ги изследваме.