«Дискретті математика бойынша оқулық dnf, sdnf, knf, sknf. Логикалық функцияның конъюнктивті қалыпты формасы арқылы логикалық функциялардың арнайы ұсынылуы
Кез келген логикалық формула үшін сәйкестікті түрлендірулерді пайдалана отырып, оған эквивалентті шексіз көп формулаларды құрастыруға болады. Логика алгебрасында негізгі міндеттердің бірі канондық формаларды (яғни, бір ережеге, канонға сәйкес құрастырылған формулаларды) іздеу болып табылады.
Егер логикалық функция айнымалыларды дизъюнкция, конъюнкция және терістеу арқылы өрнектелсе, онда бейнелеудің бұл түрі қалыпты деп аталады.
Қалыпты формалардың ішінде мінсіз қалыпты формалар (функциялар бірегей түрде жазылатын формалар) ерекшеленеді.
Керемет дизъюнктивті қалыпты пішін (PDNF)
Анықтама. Формула белгілі бір айнымалылар санының қосылуы немесе олардың теріске шығарулары арқылы жасалса, оны элементар конъюнктура деп атайды.
Мысалдар: y, ¬ y, x 1 ∧ ¬ x 2 ∧ x 3 ∧ x 4
Анықтама. Формула қайталанбайтын элементар қосылыстардың дизъюнкциясы болса, ол дизъюнктивті қалыпты форма (DNF) деп аталады.
DNF келесі түрде жазылады: F 1 ∨ F 2 ∨ ... ∨ F n , мұндағы F i – элементар конъюнктура.
Мысалдар: ¬ x 1 ∧ x 2 ∨ x 1 ∧ ¬ x 2 ∨ x 1 ∧ ¬ x 2 ∧ x 3 , ¬ y 1 ∨ y 1 ∧ y 2 ∨ ¬ y 2
Анықтама. k айнымалылардағы логикалық формула тамаша дисъюнктивтік қалыпты форма (PDNF) деп аталады, егер:
1) формула DNF болып табылады, ондағы әрбір элементар конъюнктура x 1, x 2, ..., x k айнымалыларының конъюнкциясы болып табылады және осы конъюнктураның i-ші орнында не айнымалы x i, не оның терістеуі бар. ;
2) мұндай DNF-дегі барлық элементар конъюнктуралар жұптық түрде ерекшеленеді.
Мысалы: (¬ x 1 ∧ x 2 ∧ x 3) ∨ (x 1 ∧ ¬ x 2 ∧ x 3) ∨ (x 1 ∧ x 2 ∧ ¬ x 3)
Мінсіз конъюнктивті қалыпты пішін (PCNF)
Анықтама. Формула белгілі бір айнымалылар санының дизъюнкциясы немесе оларды теріске шығару арқылы түзілсе, оны элементар дизъюнкция деп атайды.
Мысалдар: ¬ x 3, x 1 ∨ x 2, x 1 ∨ x 2 ∨ ¬ x 3
Анықтама. Формула, егер ол қайталанбайтын элементар дизъюнкциялардың конъюнкциясы болса, конъюнктивті қалыпты форма (CNF) деп аталады.
CNF келесі түрде жазылады: F 1 ∧ F 2 ∧ ... ∧ F n , мұндағы F i – элементар дизъюнкция.
Мысалдар: (x 1 ∨ ¬ x 2) ∧ x 3, (x 1 ∨ x 2) ∧ (¬ x 1 ∨ x 2 ∨ x 3) ∧ (x 1 ∨ ¬ x 2 ∨ ¬ x 3)
Анықтама. k айнымалылардағы логикалық формула тамаша конъюнктивтік қалыпты форма (CPNF) деп аталады, егер:
1) формула CNF, онда әрбір элементар дизъюнкция k айнымалылардың x 1, x 2, ..., x k дизъюнкциясы болып табылады және осы дизъюнкцияның i-ші орнында не x i айнымалысы, не оның терістелуі орналасқан;
2) мұндай CNF-дегі барлық элементар дизъюнкциялар жұппен ерекшеленеді.
Мысал: (x 1 ∨ x 2 ∨ x 3) ∧ (¬ x 1 ∨ ¬ x 2 ∨ x 3)
байқа, бұл 0 немесе 1-ге тең емес кез келген логикалық функция SDNF немесе SKNF ретінде ұсынылуы мүмкін.
Ақиқат кестесін пайдаланып SDNF құру алгоритмі
- Функция мәні біреуге тең барлық кесте жолдарын таңдаңыз.
- Әрбір осындай жолға барлық айнымалылардың конъюнкциясын былай жазыңыз: егер бұл жиындағы кейбір айнымалының мәні 1-ге тең болса, онда айнымалының өзін конъюнкцияға қосамыз, әйтпесе оның терістеуін.
- Барлық шыққан жалғауларды ажырату амалдарымен байланыстырамыз.
Ақиқат кестесін пайдаланып SCNF құру алгоритмі
- Функция мәні нөлге тең кестенің барлық жолдарын таңдаңыз.
- Әрбір осындай жолға барлық айнымалылардың дизъюнкциясын былай жазыңыз: егер бұл жиында қандай да бір айнымалының мәні 0-ге тең болса, онда айнымалының өзін конъюнкцияға қосамыз, әйтпесе оны теріске шығару.
- Барлық алынған дизъюнкцияларды конъюнкция амалдарымен байланыстырамыз.
Алгоритмдерді талдау көрсеткендей, егер ақиқат кестесінің жолдарының көпшілігінде функцияның мәні 0-ге тең болса, оның логикалық формуласын алу үшін SDNF, әйтпесе - SCNF құрастырған дұрыс.
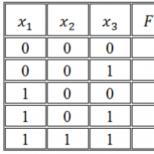
Мысал: Үш айнымалы логикалық функцияның ақиқат кестесі берілген. Осы функцияны жүзеге асыратын логикалық формуланы құрыңыз.
| x | ж | z | F(x, y, z) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Өйткені ақиқат кестесінің көптеген жолдарында функцияның мәні 1-ге тең болса, онда біз SCNF құрастырамыз. Нәтижесінде келесі логикалық формуланы аламыз:
F = (¬ x ∨ y ∨ z) ∧ (¬ x ∨ y ∨ ¬ z)
Алынған формуланы тексерейік. Ол үшін функция үшін ақиқат кестесін құрастырамыз.
| x | ж | z | ¬x | ¬ x ∨ y ∨ z | ¬z | ¬ x ∨ y ∨ ¬ z | F(x, y, z) |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
Түпнұсқа ақиқат кестесі мен логикалық формула үшін құрастырылған кестені салыстыра отырып, функция мәндерінің бағандары сәйкес келетінін байқаймыз. Бұл логикалық функцияның дұрыс құрастырылғанын білдіреді.
Пропозициялық алгебраның дизъюнктивтік және конъюнктивті қалыпты түрлері.Әрбір болжамдық логикалық функция үшін ақиқат кестесін құруға болады. Кері есеп де әрқашан шешіледі. Бірнеше анықтамаларды енгізейік.
Бастауыш жалғаулар (жалғаулар)айнымалылардың конъюнктуралары немесе әрбір айнымалы ең көп кездесетін олардың теріске шығарулары деп аталады
бір рет.
Дизьюнктивтік қалыпты форма(DNF) - элементар қосылыстардың дизъюнкциясы түріндегі формула.
Элементар дизъюнкциялар (айырулар)терістеулері бар немесе жоқ айнымалылардың дизъюнкциялары деп аталады.
Конъюнктивтік қалыпты форма(CNF) - элементар дизъюнкциялардың конъюнкциясы формасы бар формула.
Әрбір болжамды алгебра функциясы үшін дизъюнктивті және конъюнктивті қалыпты формалардың жиынын табуға болады.
DNF құру алгоритмі:
1. Баламалы түрлендіру формулаларын пайдаланып логикалық операцияларға өтіңіз.
2. Жақын терістеулері бар формулаларға, яғни терістеулері айнымалылардан жоғары емес орналасқан формулаға өтіңіз - Де Морган заңдарын қолданыңыз.
3. Жақшаларды ашыңыз - үлестірім заңдарын қолданыңыз.
4. Қайталанатын терминдерді бір-бір рет қабылдаңыз – импотенттілік заңы.
5. Жұтылу және жартылай жұтылу заңдарын қолданыңыз.
6-мысал. DNF формулаларын табыңыз: .
Буль алгебрасында бұл дұрыс екіжақтылық принципі. Ол келесідей.
Функция шақырылады қосфункциясына, егер . Анау. Берілгенге қосарланған функцияны табу үшін аргументтердің терістеулерінен функцияның терістеуін құру керек.
7-мысал.-ге қосарланған функцияны табыңыз.
Логика алгебрасының элементар функцияларының ішінде 1 - 0-ге қосарлы және керісінше, х - х-ке қосарлы, -ге қосарлы, қосарлы және керісінше.
Функцияны білдіретін F 1 формуласында біз барлық конъюнктураларды ауыстырамыз
дизъюнкция бойынша, дизъюнкция конъюнкция бойынша, 0-де 1, 0-де 1, сонда * қосарлы функциясын білдіретін F * формуласын аламыз.
Конъюнктивті қалыпты форма (CNF) DNF үшін қос тұжырымдама болып табылады, сондықтан оны келесі схема бойынша оңай құрастыруға болады:
8-мысал. CNF формуласын табыңыз: .
6-мысалдың нәтижесін пайдаланып, бізде бар
Perfect disjunctive and perfect conjunctive normal forms.Қалыпты формалардың (дизъюнктивті және конъюнктивті) түрлерінің әрқайсысында SDNF және SCNF тамаша формалар класын ажыратуға болады.
Мінсіз элементар конъюнктура терістеулі немесе терістеусіз барлық айнымалылардың логикалық туындысы болып табылады және әрбір айнымалы туындыда бір рет қана пайда болады.
Кез келген DNF барлық айнымалыларды қамтымайтын конъюнкцияларды бөлу арқылы SDNF-ге дейін қысқартылуы мүмкін, яғни. жетіспейтін айнымалы x i үшін қосу арқылы дистрибутивтік заңның көмегімен көбейтіледі
9-мысал. 6-мысалдағы DNF үшін SDNF табыңыз
Мінсіз элементар дизъюнкциятерістеулері бар немесе жоқ барлық айнымалылардың логикалық қосындысы болып табылады және әрбір айнымалы қосындыға тек бір рет енгізіледі.
Кез келген CNF конъюнктура арқылы ешбір X i айнымалысы жоқ конъюнкция мүшесін қосу және дистрибутив заңын қолдану арқылы SCNF-ге келтіруге болады.
10-мысал. KNF-ті SKNF-ке әкеліңіз:
SCNF құру үшін диаграмманы пайдалануға болады
11-мысал. 6-мысал формуласы үшін SCNF табыңыз.
Әрбір функцияның SDNF және оның үстіне бірегейі бар. Әрбір функцияның SCNF және оның үстіне бірегейі бар.
Өйткені SDNF және SKNF формулалар арқылы бірегей түрде анықталады, оларды формуланың ақиқат кестесі арқылы құруға болады.
SDNF құру үшін F 1 мәнін қабылдайтын жолдарды таңдап, олар үшін тамаша элементар жалғауларды жазу керек. Егер ақиқат кестесінің қажетті жолындағы айнымалының мәні біреуге тең болса, онда толық конъюнктурада ол терістеусіз, нөл болса, терістеумен қабылданады. Сонда тамаша жалғаулар (олардың саны кестедегі бірлік санына тең) дизъюнкция белгілері арқылы жалғанады.
Ақиқат кестесін пайдаланып SCNF құру үшін ондағы F = 0 болатын жолдарды таңдап, тамаша элементар дизъюнкцияларды жазып, содан кейін оларды конъюнкция белгілерімен қосу керек. Егер ақиқат кестесінің қажетті жолында (F=0) айнымалының мәні нөлге сәйкес келсе, онда толық сөйлемде терістеусіз, егер ол біреу болса, онда терістеумен қабылданады.
12-мысал. 6-мысал формуласы үшін ақиқат кестесін пайдаланып SDNF және SCNF табыңыз.
14-кестеде тек соңғы мән F=10101101 көрсетілген. Толық ақиқат кестесін құру арқылы осы мәлімдеменің дұрыстығын өзіңіз тексеруіңіз керек.
14-кесте
| x | ж | z | ||
Қарапайым дизъюнкция(ағыл. инклюзивті дизъюнкция) немесе дизъюнкция(Ағылшынша дизъюнкт) - бір немесе бірнеше айнымалылардың дизъюнкциясы немесе олардың теріске шығарулары, әрбір айнымалы бір реттен көп емес орын алады.
Қарапайым дизъюнкция
- толық, егер әрбір айнымалы (немесе оның теріске шығаруы) дәл бір рет пайда болса;
- монотонды, егер ол айнымалылардың терістеулерін қамтымаса.
Конъюнктивтік қалыпты форма, CNF(ағыл. конъюнктивтік қалыпты форма, CNF) логикалық функцияның бірнеше жай сөйлемнен тұратын конъюнктура пішіні болатын қалыпты пішін.
KNF мысалы:$f(x,y) = (x \lor y) \land (y \lor \neg ( z ))$
SKNF
Мінсіз конъюнктивті қалыпты форма, SCNF(Ағылшынша тамаша конъюнктивтік қалыпты пішін, PCNF) - бұл шарттарды қанағаттандыратын CNF:
- онда бірдей қарапайым дизъюнкциялар жоқ
- әрбір қарапайым дизъюнкция аяқталды
SKNF мысалы:$f(x,y,z) = (x \lor \neg ( y ) \lor z) \land (x\lor y \lor \neg ( z ))$
Теорема:Сәйкестікке тең емес кез келген $f(\vec ( x ))$ логикалық функциясы үшін оны анықтайтын SCNF бар.
Дәлелдеу:$\neg ( f ) (\vec x)$ функциясының кері мәні $f(\vec x)$ нөлге тең болатын жиындардағы біріне тең болғандықтан, $\neg ( f ) үшін SDNF (\vec x)$ келесідей жазуға болады:
$\neg ( f ) (\vec x) = \bigvee\limits_ ( f(x^ ( \sigma_ ( 1 ) ) , x^ ( \sigma_ ( 2 ) ) , ... ,x^ ( \sigma_ ( n) ) )) = 0 ) (x_ ( 1 ) ^ ( \ сигма_ ( 1 ) ) \ сына x_ ( 2 ) ^ ( \ sigma_ ( 2 ) ) \ сына ... \ сына x_ ( n ) ^ ( \ сигма_ ( n ) ) )) $, мұнда $ \sigma_ ( i ) $ $ x_ ( i ) $ кезінде теріске шығарудың бар немесе жоқтығын білдіреді.
Өрнектің сол және оң жақтарының инверсиясын табайық:
$ f(\vec x) = \neg (( \bigvee\limits_ ( f(x^ ( \sigma_ ( 1 ) ) , x^ ( \sigma_ ( 2 ) ) , ... ,x^ ( \sigma_ ( n) ) )) = 0 ) (x_ ( 1 ) ^ ( \ сигма_ ( 1 ) ) \ сына x_ ( 2 ) ^ ( \ sigma_ ( 2 ) ) \ сына ... \ сына x_ ( n ) ^ ( \ сигма_ ( n ) ))) ))) $
Оң жағында алынған өрнекке де Морган ережесін екі рет қолданып, мынаны аламыз: $ f(\vec x) = \bigwedge \limits_ ( f(x^ ( \sigma_1 ) , x^ ( \sigma_2 ) , \dots ,x ^ ( \ sigma_n )) = 0 ) $ $(\neg ( x_1^ ( \sigma_1 ) ) \vee \neg ( x_2^ ( \sigma_2 ) ) \vee \dots \vee \neg ( x_n^ ( \sigma_n )) ) $
Соңғы өрнек SKNF болып табылады. SCNF бірдей нөлге тең емес кез келген функция үшін құрастыруға болатын SDNF-тен алынғандықтан, теорема дәлелденді.
Ақиқат кестесін пайдаланып SCNF құру алгоритмі
- Ақиқат кестесінде функцияның мәні $0$ тең болатын айнымалылар жиынын белгілейміз.
- Әрбір белгіленген жиын үшін барлық айнымалылардың дизъюнкциясын келесі ереже бойынша жазамыз: егер қандай да бір айнымалының мәні $0$ болса, онда айнымалының өзін дизъюнкцияға қосамыз, әйтпесе оны теріске шығару.
- Барлық алынған дизъюнкцияларды конъюнкция амалдарымен байланыстырамыз.
Медиана үшін SCNF құру мысалы
1). Ақиқат кестесінде функцияның мәні $0$ тең болатын айнымалылар жиынын белгілейміз.
| x | ж | z | $ \langle x,y,z \rangle $ |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
2). Әрбір белгіленген жиын үшін біз барлық айнымалылардың конъюнкциясын келесі ереже бойынша жазамыз: егер қандай да бір айнымалының мәні $0$ болса, онда айнымалының өзін дизъюнкцияға қосамыз, әйтпесе оны теріске шығару.
| x | ж | z | $ \langle x,y,z \rangle $ | |
| 0 | 0 | 0 | 0 | $(x \lor y \lor z)$ |
| 0 | 0 | 1 | 0 | $(x \lor y \lor \neg ( z ))$ |
| 0 | 1 | 0 | 0 | $(x \lor \neg ( y ) \lor z)$ |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | $(\neg ( x ) \lor y \lor z)$ |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 |
3). Барлық алынған дизъюнкцияларды конъюнкция амалдарымен байланыстырамыз.
$ \langle x,y,z \rangle = (x \lor y \lor z) \land (\neg ( x ) \lor y \lor z) \land (x \lor \neg ( y ) \lor z) \land (x \lor y \lor \neg ( z ))$
Кейбір функциялар үшін SKNF мысалдары
Пирс көрсеткісі: $ x \downarrow y = (\neg ( x ) \lor (y )) \land (( x ) \lor \neg (y )) \land (\neg ( x ) \lor \neg ( y ) ) $
Эксклюзивті немесе: $ x \oplus y \oplus z = (\neg ( x ) \lor \neg ( y ) \lor z) \land (\neg ( x ) \lor y \lor \neg ( z )) \land (x \lor \neg ( y ) \lor \neg ( z )) \land (x \lor y \lor z)$
Қалыпты пішін логикалық формулада элементар емес формулалардың импликация, эквиваленттік және терістеу белгілері болмайды.
Қалыпты пішін екі түрде болады:
конъюнктивті қалыпты форма (CNF)-- бірнеше дизъюнкциялардың жалғауы, мысалы, $\left(A\vee \overline(B)\vee C\right)\wedge \left(A\vee C\right)$;
дизъюнктивті қалыпты форма (DNF)-- бірнеше жалғаулардың дизъюнкциясы, мысалы, $\left(A\сына \overline(B)\сына C\right)\vee \left(B\сына C\right)$.
SKNF
Мінсіз конъюнктивті қалыпты пішін (PCNF) үш шартты қанағаттандыратын CNF болып табылады:
құрамында бірдей элементар дизъюнкциялар жоқ;
дизъюнкциялардың ешқайсысында бірдей айнымалылар жоқ;
әрбір элементар дизъюнкцияда берілген CNF құрамына кіретін әрбір айнымалы бар.
Бірдей ақиқат емес кез келген логикалық формуланы SKNF-де көрсетуге болады.
Ақиқат кестесін пайдаланып СКНФ құру ережелері
Функциясы 0-ге тең айнымалылардың әрбір жиыны үшін қосынды жазылады, ал 1 мәні бар айнымалылар терістеумен қабылданады.
SDNF
Керемет дизъюнктивті қалыпты пішін (PDNF) үш шартты қанағаттандыратын DNF болып табылады:
құрамында бірдей элементар жалғаулар болмайды;
қосылғыштардың ешқайсысында бірдей айнымалылар жоқ;
Әрбір элементар конъюнктурада берілген DNF-ге және бірдей ретпен енгізілген әрбір айнымалы бар.
Бірдей жалған емес кез келген логикалық формула SDNF-де және бірегей түрде ұсынылуы мүмкін.
Ақиқат кестесін пайдаланып SDNF құру ережелері
Функциясы 1-ге тең айнымалылардың әрбір жиыны үшін туынды жазылады, ал 0 мәні бар айнымалылар терістеумен қабылданады.
SCNF және SDNF табу мысалдары
1-мысал
Логикалық функцияны оның ақиқат кестесін пайдаланып жаз:
1-сурет.
Шешімі:
SDNF құру ережесін қолданайық:

2-сурет.
Біз SDNF аламыз:
SCNF құру ережесін қолданайық.
Мысал. CNF формулаларын табыңыз ![]()
~ ![]() ~
~
![]()
SDNF-тің тамаша дизъюнктивті қалыпты түрін келесі алгоритм арқылы құруға болады:
1. = 1. DNF алгоритмі
2. = 2. DNF алгоритмі
3. = 3. DNF алгоритмі
4. = 4. DNF алгоритмі
5. Бірдей жалған терминдерді, яғни пішін шарттарын алып тастаңыз
6. Қалған шарттарды жетіспейтін айнымалылармен аяқтаңыз
7. 4-тармақты қайталаңыз.
Мысал. SDNF формулаларын табыңыз.
![]() ~
~
![]()
![]()
![]()
![]()
SCNF құру үшін келесі схеманы қолдануға болады:
Мысал. SDNF формулаларын табыңыз.
![]() ~
~
![]()
Белгілі (2.11, 2.12 теоремалар) SDNF және SCNF формула бойынша біркелкі анықталған, сондықтан оларды формуланың ақиқат кестесін пайдаланып тұрғызуға болады.
Ақиқат кестесіне сәйкес SDNF және SCNF құру схемасы формула үшін төменде келтірілген. ![]() ~ :
~ :
| | ||||
| 1 0 1 0 1 1 0 1 | SDNF; SKNF. |
2.2. Жаттығу.
2.2.1 Төменде логикалық өрнектер берілген. Бульдің логикалық заңдарын қолданып, нұсқаңыздың өрнектерін барынша жеңілдетіңіз. Содан кейін оңайлатылған өрнекті түпнұсқамен салыстыру үшін ақиқат кестелерін пайдаланыңыз.






2.2.2. f 1 және f 2 эквиваленттілігі туралы мәселені SDNF-ге келтіру арқылы нақтылаңыз (1-кесте).
2.2.3. Жалпыланған және логикалық принципті пайдаланып f 3 үшін қос функцияны табыңыз (1-кесте). Нәтижелерді салыстырыңыз.
| № | f 1 | f 2 | f 3 |
| | |||
| |
|||
| | |||
| | |||
| | |||
| | |
||
| | |
||
| |
|||
| | |||
| | |||
| |
|||
| | |||
| | |
||
| | |||
| |
2.3. Бақылау сұрақтары.
2.3.1. Мәлімдемені анықтаңыз.
2.3.2. Мәлімдемедегі негізгі операцияларды көрсетіңіз.
2.3.3. Ақиқат кестесі дегеніміз не?
2.3.4. Келесі формулалар үшін ақиқат кестелерін құрыңыз:
~ ~ ![]() ~ ;
~ ;
2.3.5. Амалдарды орындау тәртібі туралы конвенцияларды ескере отырып, формулалардағы «қосымша» жақшаларды және «» белгісін алып тастаңыз:
![]() ;
;
2.3.6. Эквивалентті түрлендірулерді қолданып, формулалардың бірдей ақиқаттығын дәлелдеңдер:
2.3.7. Қосарлы формулаларды табыңыз:
![]()
![]()
![]() )
)
2.3.8. мінсіз DNF (SDNF) пішініне келесі формулаларды азайтыңыз:
![]() ~
~
2.3.9. мінсіз CNF (SCNF) пішініне келесі формулаларды азайтыңыз:
![]()
![]() ~
~
![]()
![]()
Зертханалық жұмыс No3
Тақырыбы:«Бульдік функцияларды минимизациялау. Логика»
Мақсат:Логикалық функцияларды минимизациялау әдістерімен жұмыс істеудің практикалық дағдыларын меңгеру.
3.1. Теориялық ақпарат.
Минималды формалар
Көрсетілгендей, кез келген логикалық функция мінсіз қалыпты формада (диъюнктивтік немесе конъюнктивтік) ұсынылуы мүмкін. Сонымен қатар, мұндай бейнелеу функцияның кестелік спецификациясынан оның аналитикалық өрнекіне көшудің алғашқы қадамы болып табылады. Бұдан әрі біз дизъюнктивтік формадан шығамыз және қостық принципі негізінде конъюнктивтік форма үшін сәйкес нәтижелер алынады.
Логикалық схемаларды логикалық негізде синтездеудің канондық мәселесі логикалық функцияларды минимумға келтіруге келеді, яғни. әріптердің ең аз санын (айнымалылар және олардың терістеулері) қамтитын дизъюнктивтік қалыпты формада көрсету. Мұндай формалар минималды деп аталады. Канондық синтезде сигналдар да, олардың инверсиялары да тізбектің кірістеріне беріледі деп болжанады.
Дизъюнктивтік қалыпты формада берілген формула желімдеу операциясы мен сіңіру операциясын қайталап қолдану арқылы жеңілдетілген және (конъюнктивтік қалыпты форма үшін қосарлы сәйкестіктер келесідей болады: және ). Мұнда және кез келген буль алгебра формуласы ретінде түсінуге болады. Нәтижесінде біз одан әрі түрлендірулер мүмкін болмайтын аналитикалық өрнекке келеміз, яғни. біз тұйық пішінді аламыз.
Тұйық формалардың ішінде минималды дизъюнктивтік форма да бар және ол бірегей болмауы мүмкін. Берілген тұйық пішіннің минималды екеніне көз жеткізу үшін барлық тұйық пішіндерді тауып, оларды құрамындағы әріптер саны бойынша салыстыру керек.
Мысалы, функция идеалды қалыпты дизъюнктивті түрде берілсін:
Терминдерді топтап, жапсыру операциясын қолданып, бізде .
Басқа топтастыру әдісімен біз мыналарды аламыз:
Тұйық пішіндердің екеуі де аз емес. Минималды пішінді алу үшін бастапқы формуладағы бір терминді қайталауды болжау керек (бұл әрқашан жасалуы мүмкін, өйткені ). Бірінші жағдайда мұндай мүше болуы мүмкін. Содан кейін. Терминді қосу арқылы біз мынаны аламыз: . Барлық мүмкін нұсқаларды қарап шыққаннан кейін, сіз соңғы екі пішіннің минималды екеніне көз жеткізе аласыз.
Бұл деңгейде формулалармен жұмыс істеу қараңғыда серуендеумен бірдей. Егер сіз осы мақсат үшін арнайы әзірленген кейбір графикалық және аналитикалық көріністер мен белгілерді пайдалансаңыз, минималды пішіндерді іздеу процесі көрнекі және мақсатты болады.
Көпөлшемді куб
-өлшемді текшенің әрбір шыңы бірлік құрамдас бөлігімен байланыстырылуы мүмкін. Демек, белгіленген төбелердің ішкі жиыны айнымалылардың логикалық функциясының -өлшемді текшесінде тамаша дизъюнктивті қалыпты пішіндегі салыстыру болып табылады. Суретте. 3.1 3.7-тармақтағы функция үшін осындай салыстыруды көрсетеді.

3.1-сурет Үш өлшемді текшеде SDNF-де ұсынылған функцияны көрсету
Кез келген дизъюнктивтік қалыпты пішінде берілген айнымалылар функциясын көрсету үшін оның минитерминдері мен -өлшемді текше элементтері арасында сәйкестікті орнату қажет.
(-1) дәрежелі минитерминді дәреженің екі минитерминін (бірлікті құраушы) желімдеу нәтижесі ретінде қарастыруға болады, яғни. ![]() , Өлшемді текшеде бұл төбелерді жиекпен байланыстыратын координат мәндерінде ғана ерекшеленетін екі төбені ауыстыруға сәйкес келеді (жиек оған түскен төбелерді жабады деп айтылады). Осылайша, (-1)-ші ретті минитермдер -өлшемді текшенің жиектеріне сәйкес келеді. Сол сияқты, (-2)-ші ретті минитерминдердің сәйкестігі - өлшемді текшенің беттерімен белгіленеді, олардың әрқайсысы төрт шыңды (және төрт жиекті) қамтиды.
, Өлшемді текшеде бұл төбелерді жиекпен байланыстыратын координат мәндерінде ғана ерекшеленетін екі төбені ауыстыруға сәйкес келеді (жиек оған түскен төбелерді жабады деп айтылады). Осылайша, (-1)-ші ретті минитермдер -өлшемді текшенің жиектеріне сәйкес келеді. Сол сияқты, (-2)-ші ретті минитерминдердің сәйкестігі - өлшемді текшенің беттерімен белгіленеді, олардың әрқайсысы төрт шыңды (және төрт жиекті) қамтиды.
Өлшемдерімен сипатталатын -өлшемді текше элементтері -текшелер деп аталады. Сонымен, төбелер 0-куб, жиектер 1-куб, беттер 2-куб, т.б. Жоғарыда келтірілген пайымдауды жалпылай отырып, айнымалылар функциясы үшін дизъюнктивті қалыпты формадағы ()-ші дәрежелі минимерді -кубпен берілген деп болжауға болады, ал әрбір -текше оның өлшемімен байланысты барлық төменгі өлшемді текшелерді қамтиды. шыңдары. Мысал ретінде суретте. 3.2 үш айнымалының функциясын көрсетеді. Мұнда минитерминдер 1-кубқа () сәйкес келеді, ал минитерм 2-кубпен () берілген.

Сурет 3.2 Функцияны қамту ![]()
Сонымен, кез келген дизъюнктивті қалыпты пішін бірлік құраушыларына (0-текше) сәйкес барлық шыңдарды қамтитын -текшелер жиыны арқылы -өлшемді текшеге бейнеленеді. Керісінше тұжырым да дұрыс: егер -кубтардың белгілі бір жиыны функцияның бірлік мәндеріне сәйкес келетін барлық шыңдар жиынын қамтыса, онда осы -кубтарға сәйкес келетін минитерминдердің дизъюнкциясы бұл функцияның дизъюнктивті нормадағы өрнегі болып табылады. пішін. Мұндай текшелер жиынтығы (немесе олардың сәйкес минитерминдері) функцияның жабынын құрайды деп айтылады.
Минималды пішінге деген ұмтылыс интуитивті түрде мұндай жабынды іздеу ретінде түсініледі, оның текшелерінің саны азырақ, ал олардың өлшемі үлкенірек болады. Минималды формаға сәйкес келетін қамтуды минималды қамту деп атайды. Мысалы, суреттегі жабу функциясы үшін. 3.3 ең аз үлгілерге сәйкес келеді ![]() Және
Және ![]() .
.

Күріш. 3.3 Функцияларды қамту.
сол – ![]() ; оң жақта –
; оң жақта – ![]()
 Өлшемді текшеде функцияны көрсету анық және қарапайым болған кезде болады. Төрт өлшемді текшені суретте көрсетілгендей бейнелеуге болады. 3.4, ол төрт айнымалының функциясын және оның өрнекке сәйкес келетін минималды қамтуын көрсетеді
Өлшемді текшеде функцияны көрсету анық және қарапайым болған кезде болады. Төрт өлшемді текшені суретте көрсетілгендей бейнелеуге болады. 3.4, ол төрт айнымалының функциясын және оның өрнекке сәйкес келетін минималды қамтуын көрсетеді ![]() . Бұл әдісті қолдану оның барлық артықшылықтарын жоғалтатын күрделі конструкцияларды қажет етеді.
. Бұл әдісті қолдану оның барлық артықшылықтарын жоғалтатын күрделі конструкцияларды қажет етеді.
Күріш. 3.4 Функция дисплейі ![]() төрт өлшемді текшеде
төрт өлшемді текшеде
Карно карталары
Логикалық функцияларды графикалық түрде көрсетудің басқа әдісі қолданылады Карно карталары, олар арнайы ұйымдастырылған корреспонденциялық кестелер. Кестенің бағандары мен жолдары екі айнымалыдан аспайтын мәндердің барлық мүмкін жиындарына сәйкес келеді және бұл жиындар әрбір келесі айнымалылардың тек біреуінің мәні бойынша алдыңғысынан ерекшеленетіндей ретпен орналастырылған. . Осының арқасында кестенің көршілес ұяшықтары көлденең және тігінен тек бір айнымалының мәнімен ерекшеленеді. Кестенің шетінде орналасқан ұяшықтар да іргелес болып саналады және бұл қасиетке ие. Суретте. 3.5-суретте екі, үш, төрт айнымалыға арналған Карно карталары көрсетілген.
 |
|||||
 |
|||||
 |
|||||
Күріш. 3.5 Екі, үш және төрт айнымалыларға арналған Карно карталары
Кәдімгі ақиқат кестелеріндегідей, функция 1 мәнін қабылдайтын жиындардың ұяшықтары бірліктермен толтырылады (нөлдер әдетте сәйкес келмейді, олар бос ұяшықтарға сәйкес келеді). Мысалы, суретте. 3.6, Афункциясы үшін Карнау картасын көрсетеді, оның дисплейі төрт өлшемді текшеде суретте берілген. 3.4. Заттарды жеңілдету үшін айнымалыға арналған 1 мәндеріне сәйкес келетін жолдар мен бағандар сол айнымалыны көрсететін жақшамен бөлектеледі.
 |
|||
 |
|||
Күріш. 3.6 Карно картасында төрт айнымалы функцияны көрсету
(а) және оның ең аз қамтылуы (b)
Функцияларды салыстыру арасында n-өлшемді текше және Карно картасы бір-біріне сәйкес келеді. Карно картасында с-текше қатарға, бағанға, шаршыға немесе тіктөртбұрышқа (картаның қарама-қарсы шеттерінің жақындығын ескере отырып) орналастырылған 2 көрші ұяшықтар жиынтығына сәйкес келеді. Сондықтан жоғарыда көрсетілген барлық ережелер (тармақты қараңыз. көпөлшемді куб), Karnaugh карталары үшін жарамды. Сонымен, суретте. 3.6, бминималды дизъюнктивтік формаға сәйкес карта бірліктерінің қамтылуын көрсетеді ![]() қарастырылып отырған функция.
қарастырылып отырған функция.
Карнау картасынан минитерминдерді оқу қарапайым ережеге бағынады. Жасушалардың түзілуі с-текше, министр бер (n–s)-оларды қамтитын разряд (n–s)сол мәндерді сақтайтын айнымалылар с-cube, мұндағы 1 мәні айнымалылардың өздеріне, ал 0 мәні олардың терістеулеріне сәйкес келеді. Өз мәндерін сақтамайтын айнымалылар с-куб, минимумда жоқ. Оқудың әртүрлі тәсілдері функцияның дисъюнктивтік қалыпты формада әртүрлі бейнеленуіне әкеледі (ең оң жақтағы минималды) (3.7-сурет).
 |  |
||||||||
 |
|||||||||
Карно карталарын пайдалану картаға түсірумен салыстырғанда қарапайым конструкцияларды қажет етеді n-өлшемді текше, әсіресе төрт айнымалы жағдайда. Бес айнымалы функцияларды көрсету үшін төрт айнымалыға арналған екі Карно картасы, ал алты айнымалы функция үшін осындай төрт карта пайдаланылады. Айнымалылар санының одан әрі көбеюімен Карно карталары іс жүзінде жарамсыз болып қалады.
Әдебиетте танымал Veitch карталарыОлар айнымалы мәндер жиынының әртүрлі ретімен ғана ерекшеленеді және Карно карталарымен бірдей қасиеттерге ие.
Текшелер кешені
Айнымалылардың үлкен саны бар графикалық әдістердің сәйкессіздігі логикалық функцияларды көрсету үшін әртүрлі аналитикалық әдістермен өтеледі. Осындай өкілдіктердің бірі текшелер кешені, көпөлшемді логикалық кеңістік терминологиясын арнайы әзірленген символизммен үйлестіре пайдалану.
). Бірліктің құрамдас бөліктеріне сәйкес келетін 0-текшелер функция бірлікке тең болатын айнымалы мәндер жиынымен көрсетіледі. Жазбада анық


Күріш. 3.8 Үш айнымалы функцияның текшелер кешені ( А) және оның символдық көрінісі ( б)
Текшелер кешені қалыптасады максималды функцияны қамту. Оның барлығын қоспағанда с-өлшемі жоғары текшелермен жабылған текшелер, біз тұйық пішіндерге сәйкес жабындарды аламыз. Сонымен, қарастырылып отырған мысал үшін (3.8-сурет) бізде тұйық жабын бар
 ,
,
функциясына сәйкес келеді ![]() . Бұл жағдайда бұл қамту минималды болады.
. Бұл жағдайда бұл қамту минималды болады.
Екі логикалық функция үшін ажырату операциясы олардың текше кешендерінің бірігуіне, ал конъюнкция операциясы олардың текше кешендерінің қиылысына сәйкес келеді. Функцияны теріске шығару текшелер кешенінің толықтауышына сәйкес келеді, яғни және функция 0 мәнін алатын барлық шыңдармен анықталады. Осылайша, алгебрасы арасында бір-біріне сәйкестік (изоморфизм) бар. Логикалық функциялар және текшелер кешендерін көрсететін логикалық жиындар.
Функцияны текшелер кешендері түрінде көрсету визуалдылығы азырақ, бірақ оның маңызды артықшылығы – айнымалылар санына шектеулер жойылады және компьютерлерді пайдалану кезінде ақпаратты кодтау жеңілдетіледі.
Логикалық функцияларды азайту
Мәселенің тұжырымы.Логикалық негізде тізбекті минимизациялау минималды қамтуға сәйкес келетін минималды дизъюнктивті пішінді табуға келеді. Қалыпты түрдегі хаттардың жалпы саны қамту құнымен көрсетіледі ![]() , мұндағы n айнымалының берілген функциясын жабуды құрайтын текшелер саны. Ең төменгі қамту оның бағасының ең төменгі мәнімен сипатталады.
, мұндағы n айнымалының берілген функциясын жабуды құрайтын текшелер саны. Ең төменгі қамту оның бағасының ең төменгі мәнімен сипатталады.
Әдетте, азайту мәселесі екі қадаммен шешіледі. Біріншіден, біз ең үлкен өлшемдегі барлық текшелерді қамтитын кішірейтілген мұқабаны іздейміз, бірақ бұл мұқабаның кез келген текшесі жабылған бір ғана текшені қамтымайды. Сәйкес дизъюнктивті нормаль түрі редукцияланған, ал оның минитерминдері жай импликанттар деп аталады. Берілген функция үшін қысқартылған қамту бірегей болып табылады, бірақ ол текшелердің кейбірі басқа текшелердің жинақтарымен қамтылғанына байланысты артық болуы мүмкін.
Екінші қадамда ең аз пішіндер таңдап алынатын қысқартылған дизъюнктивті қалыпты формалардан тұйыққа көшу жүзеге асырылады. Тұйық пішіндер қысқартылған жабыннан барлық артық текшелерді алып тастау арқылы қалыптасады, онсыз текшелердің қалған жинағы бұрынғысынша берілген функцияның жабынын құрайды, бірақ текшелердің кез келгенін одан әрі алып тастағанда, ол енді барлығының жиынын қамтымайды. функцияның жалғыз мәндеріне сәйкес келетін шыңдар, яғни ол жабу болуды тоқтатады.
Басқа текшелермен қамтылмаған берілген функцияның шыңдарын қамтитын қысқартылған қамту текшесі артық болмайды және әрқашан ең аз қамтуға қосылады. Мұндай текше, оның сәйкес импликанты сияқты, экстремалды (негізгі импликант) деп аталады, ал оны қамтитын шыңдар жойылған шыңдар деп аталады. Экстремалдар жиынтығы жабынның өзегін құрайды, қысқартылған жабыннан минималдыға көшкен кезде, ең алдымен, барлық экстремалды оқшаулау қажет екені анық. Егер экстремалдар жиынтығы жабын түзбесе, онда ол қысқартылған жабыннан текшелермен жабу үшін толықтырылады.
Берілген анықтамалар суретте көрсетілген. 3.9, мұнда қысқартылған қамту (3.9а-суретті қараңыз, ) және минималды қамту (3.9б-сурет) және (3.9, б-суретті қараңыз) төмендегідей көрсетіледі.