Forma normală conjunctivă a unei funcții logice. Reprezentări speciale ale funcțiilor booleene. Exemple de sknf pentru unele funcții
Definiția 1.Monomiul conjunctiv (conjuncție elementară) de variabile este conjuncția acestor variabile sau negațiile lor.
De exemplu, este o conjuncție elementară.
Definiția 2.Monomiul disjunctiv (disjuncția elementară) din variabile este disjuncția acestor variabile sau negațiile lor.
De exemplu, este o disjuncție elementară.
Definiția 3. O formulă care este echivalentă cu o formulă de algebră propozițională dată și este o disjuncție de monomii conjunctive elementare se numește forma normală disjunctivă(DNF) din această formulă.
De exemplu,– DNF.
Definiția 4. O formulă care este echivalentă cu o formulă de algebră propozițională dată și este o conjuncție de monomii disjunctive elementare se numește forma normală conjunctivă(CNF) din această formulă.
De exemplu, – KNF.
Pentru fiecare formulă de algebră propozițională se poate găsi un set de forme normale disjunctive și conjunctive.
Algoritm pentru construirea formelor normale
Folosind echivalentele algebrei logice, înlocuiți toate operațiile de bază din formula: conjuncție, disjuncție, negație:
Scapa de dublele negative.
Aplicați, dacă este necesar, proprietățile formulelor de distributivitate și absorbție la operațiile de conjuncție și disjuncție.
2.6. Formele normale disjunctive perfecte și conjunctive perfecte
Orice funcție booleană poate avea multe reprezentări sub formă de DNF și CNF. Un loc special printre aceste reprezentări îl ocupă DNF perfect (SDNF) și CNF perfect (SCNF).
Definiția 1. Forma normală disjunctivă perfectă(SDNF) este un DNF în care fiecare monom conjunctiv conține fiecare variabilă din mulțime exact o dată, fie el însuși, fie negația sa.
Din punct de vedere structural, SDNF pentru fiecare formulă de algebră propozițională redusă la un DNF poate fi definit după cum urmează:
Definiția 2. Forma normală disjunctivă perfectă(SDNF) a unei formule de algebră propozițională se numește DNF, care are următoarele proprietăți:
Definiția 3. Forma normală conjunctivă perfectă(SCNF) este un CNF în care fiecare monom disjunctiv conține fiecare variabilă din mulțime exact o dată și apare fie el însuși, fie negația sa.
Din punct de vedere structural, SCNF pentru fiecare formulă de algebră propozițională redusă la CNF poate fi definit după cum urmează.
Definiția 4. Forma normală conjunctivă perfectă(SCNF) a unei formule de algebră propozițională dată se numește CNF care satisface următoarele proprietăți.
Teorema 1. Fiecare funcție booleană a variabilelor care nu este identic falsă poate fi reprezentată în SDNF și într-un mod unic.
Metode de găsire a SDNF
1a metoda
a 2-a metoda
selectați liniile în care formula ia valoarea 1;
compunem o disjuncție de conjuncții cu condiția ca, dacă o variabilă este inclusă în conjuncția cu valoarea 1, atunci notăm această variabilă; dacă este cu valoarea 0, atunci negația ei. Primim SDNF.
Teorema 2. Fiecare funcție booleană a variabilelor care nu este identic adevărată poate fi reprezentată în SCNF și într-un mod unic.
Metode de găsire a SCNF
1a metoda– folosind transformări echivalente:
a 2-a metoda– folosind tabele de adevăr:
selectați liniile în care formula ia valoarea 0;
compunem o conjuncție de disjuncții cu condiția ca, dacă o variabilă este inclusă în disjuncție cu valoarea 0, atunci notăm această variabilă; dacă este cu valoarea 1, atunci negația ei. Primim SKNF.
Exemplul 1. Construiți funcții CNF.
Soluţie
Să eliminăm conectivul „” folosind legile de transformare a variabilelor:
= /legile lui de Morgan și dubla negație/ =
/legi distributive/ =
Exemplul 2. Dați formula lui DNF.
Soluţie
Să exprimăm operații logice folosind și:
= /să clasificăm negația ca variabile și să reducem dublele negative/ =
= /legea distributivității/ .
Exemplul 3. Scrieți formula în DNF și SDNF.
Soluţie
Folosind legile logicii, reducem această formulă la o formă care conține doar disjuncții ale conjuncțiilor elementare. Formula rezultată va fi DNF dorită:
Pentru a construi SDNF, să creăm un tabel de adevăr pentru această formulă:
Marcam acele rânduri ale tabelului în care formula (ultima coloană) ia valoarea 1. Pentru fiecare astfel de rând, scriem o formulă care este adevărată pe setul de variabile din acest rând:
linia 1: ;
linia 3: ;
linia 5: .
Disjuncția acestor trei formule va lua valoarea 1 numai pe seturile de variabile din rândurile 1, 3, 5 și, prin urmare, va fi forma normală disjunctivă perfectă dorită (PDNF):
Exemplul 4. Aduceți formula la SKNF în două moduri:
a) folosind transformări echivalente;
b) folosind un tabel de adevăr.
Soluţie:
Să transformăm a doua disjuncție elementară:
Formula arată astfel:
b) întocmește un tabel de adevăr pentru această formulă:
Marcam acele rânduri ale tabelului în care formula (ultima coloană) ia valoarea 0. Pentru fiecare astfel de rând, scriem o formulă care este adevărată pe setul de variabile din acest rând:
randul 2: ;
linia 6: .
Conjuncția acestor două formule va lua valoarea 0 numai pe seturile de variabile din rândurile 2 și 6 și, prin urmare, va fi forma normală conjunctivă perfectă dorită (PCNF):
Întrebări și sarcini pentru soluții independente
1. Folosind transformări echivalente, reduceți formulele la DNF:
2. Folosind transformări echivalente, aduceți formulele la CNF:
3. Folosind a doua lege distributivă, convertiți DNF în CNF:
A) ![]() ;
;
4. Convertiți DNF-urile date în SDNF-uri:
5. Convertiți CNF-ul dat în SCNF:
6. Pentru formule logice date, construiți SDNF și SCNF în două moduri: folosind transformări echivalente și folosind un tabel de adevăr.
b) ![]() ;
;
Disjuncție simplă(ing. disjuncție inclusivă) sau disjuncție(Disjunct în engleză) este o disjuncție a uneia sau mai multor variabile sau a negațiilor acestora, fiecare variabilă care apare nu mai mult de o dată.
Disjuncție simplă
- deplin, dacă fiecare variabilă (sau negația ei) apare exact o dată;
- monoton, dacă nu conține negații ale variabilelor.
Forma normală conjunctivă, CNF(eng. forma normală conjunctivă, CNF) o formă normală în care o funcție booleană are forma unei conjuncții de mai multe propoziții simple.
Exemplu KNF:$f(x,y) = (x \lor y) \land (y \lor \neg ( z ))$
SKNF
Forma normală conjunctivă perfectă, SCNF(forma normală conjunctivă perfectă engleză, PCNF) este un CNF care îndeplinește condițiile:
- nu conţine disjuncţii simple identice
- fiecare disjuncție simplă este completă
Exemplu SKNF:$f(x,y,z) = (x \lor \neg ( y ) \lor z) \land (x\lor y \lor \neg ( z ))$
Teorema: Pentru orice funcție booleană $f(\vec ( x ))$ care nu este egală cu identitatea, există un SCNF care o definește.
Dovada: Deoarece inversul funcției $\neg ( f ) (\vec x)$ este egal cu unul pe acele mulțimi pe care $f(\vec x)$ este egal cu zero, atunci SDNF pentru $\neg ( f ) (\vec x)$ poate fi scris după cum urmează:
$\neg ( f ) (\vec x) = \bigvee\limits_ ( f(x^ ( \sigma_ ( 1 ) ) , x^ ( \sigma_ ( 2 ) ) , ... ,x^ ( \sigma_ ( n ) )) = 0 ) (x_ ( 1 ) ^ ( \sigma_ ( 1 ) ) \wedge x_ ( 2 ) ^ ( \sigma_ ( 2 ) ) \wedge ... \wedge x_ ( n ) ^ ( \sigma_ ( n ) ) )) $, unde $ \sigma_ ( i ) $ denotă prezența sau absența negației la $ x_ ( i ) $
Să găsim inversarea părților stânga și dreaptă ale expresiei:
$ f(\vec x) = \neg (( \bigvee\limits_ ( f(x^ ( \sigma_ ( 1 ) ) ), x^ ( \sigma_ ( 2 ) ) , ... ,x^ ( \sigma_ ( n ) )) = 0 ) (x_ ( 1 ) ^ ( \sigma_ ( 1 ) ) \wedge x_ ( 2 ) ^ ( \sigma_ ( 2 ) ) \wedge ... \wedge x_ ( n ) ^ ( \sigma_ ( n ) ) )) )) $
Aplicând regula lui de Morgan de două ori expresiei obținute în partea dreaptă, obținem: $ f(\vec x) = \bigwedge \limits_ ( f(x^ ( \sigma_1 ) , x^ ( \sigma_2 ) , \dots ,x ^ ( \ sigma_n )) = 0 ) $ $(\neg ( x_1^ ( \sigma_1 ) ) \vee \neg ( x_2^ ( \sigma_2 ) ) \vee \dots \vee \neg ( x_n^ ( \sigma_n ) ) ) $
Ultima expresie este SKNF. Deoarece SCNF este obținut din SDNF, care poate fi construit pentru orice funcție care nu este identic zero, teorema este demonstrată.
Algoritm pentru construirea SCNF folosind un tabel de adevăr
- În tabelul de adevăr marchem acele seturi de variabile pentru care valoarea funcției este egală cu $0$.
- Pentru fiecare mulțime marcată, scriem disjuncția tuturor variabilelor după următoarea regulă: dacă valoarea unei variabile este $0$, atunci includem variabila însăși în disjuncție, în caz contrar negația ei.
- Conectăm toate disjuncțiile rezultate cu operațiile de conjuncție.
Un exemplu de construire a SCNF pentru mediană
1). În tabelul de adevăr marchem acele seturi de variabile pentru care valoarea funcției este egală cu $0$.
| X | y | z | $ \langle x,y,z \rangle $ |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
2). Pentru fiecare mulțime marcată, scriem conjuncția tuturor variabilelor după următoarea regulă: dacă valoarea unei variabile este $0$, atunci includem variabila în sine în disjuncție, în caz contrar negația ei.
| X | y | z | $ \langle x,y,z \rangle $ | |
| 0 | 0 | 0 | 0 | $(x \lor y \lor z)$ |
| 0 | 0 | 1 | 0 | $(x \lor y \lor \neg ( z ))$ |
| 0 | 1 | 0 | 0 | $(x \lor \neg ( y ) \lor z)$ |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | $(\neg ( x ) \lor y \lor z)$ |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 |
3). Conectăm toate disjuncțiile rezultate cu operațiile de conjuncție.
$ \langle x,y,z \rangle = (x \lor y \lor z) \land (\neg ( x ) \lor y \lor z) \land (x \lor \neg ( y ) \lor z) \land (x \lor y \lor \neg ( z ))$
Exemple de SKNF pentru unele funcții
Săgeata lui Peirce: $ x \downarrow y = (\neg ( x ) \lor ( y )) \land (( x ) \lor \neg ( y )) \land (\neg ( x ) \lor \neg ( y ) ) $
Exclusiv sau: $ x \oplus y \oplus z = (\neg ( x ) \lor \neg ( y ) \lor z) \land (\neg ( x ) \lor y \lor \neg ( z )) \land (x \lor \neg ( y ) \lor \neg ( z )) \land (x \lor y \lor z)$
Baza standard. Formulele elementare sunt literale. Conjuncție elementară (disjuncție). Forma normală disjunctivă (conjunctivă) și formă perfectă. Teoremă: orice funcție booleană diferită de 0 (din 1) poate fi reprezentată sub formă de SDNF (SCNF). Completitudinea bazei standard. Exemple de baze complete: baza Zhegalkin, lovitura Schaeffer, săgeata Peirce.
Baza standard este un set de trei operații de bază ale algebrei booleene: adunare (unire), înmulțire (intersecție) și negație.
Aici vom suna literal variabila x sau negația sa x și notăm xˆ. Intersecția booleană a mai multor literale definite de diferite variabile, i.e. expresie de forma X = xˆ 1 xˆ 2 . . . xˆ l, numit conjuncție elementară . Cerința ca toate variabilele să fie diferite este determinată de următoarele. Dacă o conjuncție include mai multe literale identice, atunci datorită comutativității, asociativității și idempotității conjuncției, este posibil, trecând la formula echivalentă, să se lase doar un literal (de exemplu, x 1 x 1 = x 1). Dacă conjuncția include o variabilă și negația acesteia, atunci formula este echivalentă cu constanta 0, deoarece x x = 0 și pentru orice formulă Y avem Y x x = 0.
Se numește disjuncția mai multor conjuncții elementare forma normală disjunctivă , sau DNF . De exemplu,
x 1 x 3 + x 2 x 3 x 4 + x 1 x 2 x 3 x 5 .
Dacă compoziția variabilelor din fiecare conjuncție elementară a unui DNF dat este aceeași, atunci DNF se numește perfect . Exemplul dat este un DNF care nu este perfect. Dimpotrivă, formula
x 1 x 2 x 3 x 4 +x 1 x 2 x 3 x 4 +x 1 x 2 x 3 x 4
există o formă perfectă.
Deoarece în algebra booleană adăugarea și înmulțirea sunt operații simetrice și puteți interpreta întotdeauna adunarea ca înmulțire și înmulțirea ca adunare, există un concept dual - forma normală conjunctivă (KNF ), care este o conjuncție de disjuncții elementare și formă conjunctivă perfectă (SKNF ). Din principiul dualității pentru semiinele simetrice rezultă că oricărei afirmații referitoare la DNF se răspunde printr-o afirmație duală referitoare la CNF, care se obține prin înlocuirea adunării (disjuncției) cu înmulțirea, înmulțirii (conjuncției) cu adunarea, constantă 0 cu constantă 1, constantă. 1 cu constantă 0, relație de ordine cu dual (invers) în ordine. Prin urmare, în continuare ne vom concentra pe studierea doar a DNF.
Teorema 1.4. Orice funcție booleană, alta decât constanta 0, poate fi reprezentată ca un SDNF.
◀Să fim de acord că prin x σ înțelegem formula x dacă σ = 1 și formula x dacă σ = 0. Fie funcția f(y 1 , . . . , y n) să ia valoarea 1 pe vector (t 1, . . . , t n ) (un astfel de vector se numește unitate constitutivă ). Atunci conjuncția elementară ia și valoarea 1 pe această mulțime, dar dispare pe toți ceilalți vectori booleeni n-dimensionali. Luați în considerare formula
în care suma (uniunea) se extinde la toate acele mulțimi (t 1, . . . , t n) de valori argument pe care funcția dată ia valoarea 1. Rețineți că mulțimea acestor mulțimi nu este goală, deci suma conține cel puțin un termen.
Este ușor de observat că formula Φ devine 1 pentru acele și numai pentru acele valori ale variabilelor pentru care funcția în cauză devine 1. Aceasta înseamnă că formula Ψ reprezintă funcția f.
Corolarul 1.1. Baza standard este completă.
◀ Într-adevăr, dacă o funcție nu este o constantă 0, atunci ea poate fi reprezentată fie sub forma unui SDNF, care este o formulă pe o bază standard. Constanta 0 poate fi reprezentată, de exemplu, prin formula f(x 1, x 2,. . . , x n) = x 1 x 1.
Exemplul 1.2. Se consideră o funcție de trei variabile m(x 1, x 2, x 3) (Tabelul 1.4), numită functie majoritara ̆. Această funcție evaluează la 1 dacă mai mult de jumătate din argumentele sale au valoarea 1. Prin urmare, este adesea numită funcție de vot. Să construim un SDNF pentru el.
Completitudinea bazei standard face posibilă selectarea altor sisteme complete de funcții. Completitudinea multimii F poate fi stabilita din urmatoarele consideratii. Să presupunem că fiecare dintre cele trei funcții busis standard este reprezentabilă printr-o formulă peste F . Apoi, prin teorema 1.3, identitatea F va fi completă.
Exemplul 1.3. Se numește setul de operații modulo 2 adunare, înmulțire și constantă 1 Baza Zhegalkin . Adunarea modulo 2 și înmulțirea sunt operațiile de bază ale inelului Z2; expresiile compuse cu ajutorul lor sunt polinoame peste inelul Z2. Constanta 1 în acest caz este necesară pentru a scrie termenul liber. Deoarece xx = x, atunci toți factorii din polinom au gradul 1. Prin urmare, atunci când scrieți un polinom, puteți face fără conceptul de grad. Exemple de formule pe baza Zhegalkin:
xy⊕x⊕y, x⊕1, xyz⊕xz⊕x⊕y⊕1.
Orice astfel de formulă se numește polinomul Zhegalkin. De fapt, polinomul Zhegalkin este un polinom peste inelul Z2.
Nu este dificil să construiești formule pe baza Zhegalkin, reprezentând operațiile de adunare și negație a bazei standard (înmulțirea celor două baze este comună):
x+y=x⊕y⊕xy, x =x⊕1.
Prin urmare, baza Zhegalkin este un set complet.
Se poate demonstra că pentru orice funcție booleană polinomul Zhegalkin este definit în mod unic
(mai precis, până la ordinea termenilor). Coeficienții polinomului Zhegalkin cu un număr mic de variabile pot fi găsiți folosind metoda coeficienților nedeterminați.
Exemplul 1.4. Să considerăm un set de o singură funcție - cursa Schaeffer*. Acest set este complet, după cum urmează din următoarele identități ușor de verificat:
x =x|x, xy=x|y =(x|y)|(x|y), x+y=x |y =(x|x)|(y|y).
Exemplul 1.5. O bază constând dintr-o singură funcție, săgeata Peirce, este de asemenea completă. Testul pentru aceasta este similar cu cazul accidentului vascular cerebral Schaeffer. Totuși, această concluzie poate fi făcută și pe baza principiului dualității pentru semiinele simetrice.
* Acțiunea lui Schaeffer este o operație binară, dar nu asociativă. Prin urmare, atunci când utilizați formularul infix, ar trebui să fiți atenți: rezultatul depinde de ordinea operațiunilor. În acest caz, se recomandă să indicați în mod explicit ordinea operațiilor folosind paranteze, de exemplu, scrieți (x | y) | z, nu x | y | z, deși ambele forme sunt echivalente.
Forme normale ale funcţiilor logice Reprezentarea unei funcţii booleene sub forma unei disjuncţii de termeni conjunctivi ai constituenţilor unităţii Ki 2.7 se numeşte forma normală disjunctivă a DNF a acestei funcţii. conţin exact una dintre toate variabilele logice luate cu sau fără negaţii, atunci această formă de reprezentare a unei funcţii se numeşte forma normală disjunctivă perfectă SDNF a acestei funcţii. După cum puteți vedea, atunci când compuneți o funcție SDNF, trebuie să creați o disjuncție a tuturor mintermilor pentru care funcția ia valoarea 1.
Distribuiți-vă munca pe rețelele sociale
Dacă această lucrare nu vă convine, în partea de jos a paginii există o listă cu lucrări similare. De asemenea, puteți utiliza butonul de căutare
Cursul 1.xx
Forme normale de funcții logice
Reprezentarea unei funcții booleene sub forma unei disjuncții de termeni conjunctivi (constituent unitar) K i
, (2.7)
numit forma normală disjunctivă(DNF) a acestei funcții.
Dacă toți termenii conjunctivi din DNF sunt mintermii , adică conține exact una dintre toate variabilele logice, luate cu sau fără negații, atunci această formă de reprezentare a funcției se numeșteformă normală disjunctivă perfectă(SDNF ) această funcție. Se numește SDNF perfect , deoarece fiecare termen din disjuncție include toate variabilele; disjunctiv , deoarece operația principală din formulă este disjuncția. Conceptul "formă normală” înseamnă un mod clar de a scrie o formulă care implementează o funcție dată.
Ținând cont de cele de mai sus, din Teorema 2.1 rezultă următoarea teoremă.
Teorema 2. Orice funcție booleană(nu identic 0) poate fi prezentat în SDNF, .
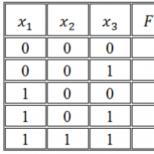
Exemplul 3. Să avem o funcție dată de tabel f (x 1 , x 2 , x 3 ) (Tabelul 10).
Tabelul 10
|
f (x 1 , x 2 , x 3 ) |
|||
Pe baza formulei (2.6) obținem:
După cum puteți vedea, atunci când compuneți o funcție SDNF, trebuie să creați o disjuncție a tuturor mintermilor pentru care funcția ia valoarea 1.
Reprezentarea unei funcții booleene sub forma unei conjuncții de termeni disjunctivi (constituent zero) D i
, (2.8)
numit forma normală conjunctivă(CNF) a acestei funcții.
Dacă toți termenii CNF disjunctivi sunt maxterms , adică conține exact una dintre toate variabilele logice ale funcției, luate cu sau fără negații, atunci un astfel de CNF se numeșteforma normală conjunctivă perfectă(SKNF) a acestei funcții.
Teorema 3. Orice funcție booleană(nu este identic cu 1) pot fi transmise la SKNF, iar o astfel de reprezentare este singura.
Demonstrarea teoremei poate fi efectuată în mod similar cu demonstrația teoremei 2.1 pe baza următoarei leme Shannon privind descompunerea conjunctivă.
Lema lui Shannon . Orice funcție booleană f (x 1, x 2, …, x m) din m variabilele pot fi reprezentate astfel:
. (2.9)
Trebuie remarcat faptul că ambele forme de reprezentare a unei funcții logice (DNF și CNF) sunt teoretic egale în capacități: orice formulă logică poate fi reprezentată atât în DNF (cu excepția zeroului identic), cât și în CNF (cu excepția celui identic). ). În funcție de situație, reprezentarea unei funcții într-o formă sau alta poate fi mai scurtă.
În practică, DNF este cel mai des folosit, deoarece această formă este mai familiară unei persoane: încă din copilărie, el este mai obișnuit să adauge produse decât să înmulțească sume (în acest din urmă caz, intuitiv are dorința de a deschide parantezele și, astfel, de a trece la DNF).
Exemplul 4. Pentru funcția f (x 1 , x 2 , x 3 ), dat de tabel. 10, scrieți-l la SKNF.
Spre deosebire de SDNF, atunci când compilați SCNF în tabelul de adevăr al unei funcții logice, trebuie să vă uitați la combinațiile de variabile la care funcția ia valoarea 0 și să creați o conjuncție a termenilor maximi corespunzători,dar variabilele trebuie luate cu inversare inversă:
Trebuie remarcat faptul că este imposibil să treceți direct de la SDNF al unei funcții la SCNF-ul acesteia sau invers. Atunci când se încearcă astfel de transformări, rezultatele sunt funcții care sunt opuse celor dorite. Expresiile pentru funcțiile SDNF și SCNF pot fi obținute direct numai din tabelul său de adevăr.
Exemplul 5. Pentru funcția f (x 1 , x 2 , x 3 ), dat de tabel. 10, încercați să comutați de la SDNF la SKNF.
Folosind rezultatul exemplului 2.3 obținem:
După cum puteți vedea, sub inversiunea generală am obținut SCNF-ul unei funcții logice, care este inversul funcției obținute în exemplul 2.4:
deoarece conține toți termenii max care nu sunt în expresia pentru SCNF a funcției luate în considerare.
1. Folosind proprietățile operațiilor (vezi Tabelul 9) identitate (), sumă modulo 2 (), implicație (), trecem la operațiile AND, OR, NOT (în baza booleană).
2. Folosind proprietățile negației și legile lui De Morgan (vezi Tabelul 9), ne asigurăm că operațiile de negație se aplică numai variabilelor individuale și nu expresiilor întregi.
3. Folosind proprietățile operațiilor logice AND și OR (vezi Tabelul 9), obținem forma normală (DNF sau CNF).
4. Dacă este necesar, trecem la forme perfecte (SDNF sau SKNF). De exemplu, pentru a obține SCNF trebuie adesea să utilizați proprietatea: .
Exemplul 6. Convertiți o funcție logică în SKNF
Efectuând pașii algoritmului de mai sus în ordine, obținem:
Folosind proprietatea de absorbție, obținem:
Astfel, am obținut funcția CNF f (x 1 , x 2 , x 3 ). Pentru a-și obține SCNF, trebuie să repeți fiecare disjuncție în care lipsește orice variabilă, de două ori cu această variabilă și cu negația ei:
2.2.6. Minimizarea funcțiilor logice
Deoarece aceeași funcție logică poate fi reprezentată ca h formule personale, apoi găsirea formei celei mai simple R mule care definește o funcție booleană, simplifică circuitul logic care implementează funcția booleană a tion. Forma minima l O functie logicaîn anumite baze putem considera unul care conține numărul minim de suprapuneri de distracție La de bază, permițând parantezele. Cu toate acestea, este dificil să construiți un eficient l algoritm pentru o astfel de minimizare pentru a obține paranteza minimă noi.
Să luăm în considerare o problemă de minimizare mai simplă în sinteza circuitelor combinaționale, în care nu căutăm forma minimă parantetică a unei funcții, ci DNF-ul ei minim. Există algoritmi simpli și eficienți pentru această sarcină.
metoda lui Quine
Funcția de minimizat este reprezentată în SDNF și i se aplică toate operațiunile de lipire incomplete posibile
, (2.10)
și apoi absorbția
, (2.11)
iar această pereche de pași se aplică în mod repetat. Astfel, este posibil să se reducă rangul termenilor. Această procedură se repetă până când nu mai rămâne niciun termen care să poată fi legat de orice alt termen.
Rețineți că partea stângă a ecuației (2.10) ar putea fi imediat minimizată într-un mod mai simplu și mai evident:
Această metodă este proastă deoarece cu o astfel de minimizare directă, termenii conjunctivi fie dispar, deși există încă cazuri posibile de utilizare a acestora pentru lipire și absorbție cu termenii rămași.
Trebuie remarcat faptul că metoda lui Quine necesită multă muncă, astfel încât probabilitatea de a face greșeli în timpul transformărilor este destul de mare. Dar avantajul său este că teoretic poate fi folosit pentru orice număr de argumente și pe măsură ce numărul de variabile crește, transformările devin mai puțin complicate.
Metoda hărții Karnaugh
Metoda hărților (tabelelor) Carnot este o modalitate mai vizuală, mai puțin laborioasă și fiabilă de a minimiza funcțiile logice, dar utilizarea sa este practic limitată la funcții de 3-4 variabile, maxim 5-6 variabile.
Harta Carnot aceasta este o formă tabelară bidimensională de reprezentare a tabelului de adevăr al unei funcții booleene, care vă permite să găsiți cu ușurință DNF-urile minime ale funcțiilor logice într-o formă vizuală grafică. Fiecare celulă a tabelului este asociată cu termenul SDNF al funcției care este minimizat și în așa fel încât orice axe de simetrie ale tabelului să corespundă zonelor care sunt reciproc inverse față de o variabilă. Această aranjare a celulelor în tabel face ușoară determinarea termenilor de lipire ai SDNF (diferă prin semnul de inversare a unei singure variabile): ei sunt localizați simetric în tabel.
Tabele de adevăr și hărți Carnaugh pentru funcțiile AND și SAU ale două benzi e Variabilele sunt prezentate în Fig. 8. În fiecare celulă a cardului este scrisă o valoare A Valoarea unei funcții din setul de valori ale argumentelor corespunzătoare acestei celule N Tovarăşe
A) ȘI b) SAU
Orez. 8. Exemplu de hărți Karnaugh pentru funcții a două variabile
În harta Karnaugh există un singur 1 pentru funcția Și, deci nu poate fi lipit de nimic. Expresia pentru funcția minimă va conține doar termenul corespunzător acestui 1:
f = x y .
În harta Carnot pentru funcția SAU există deja trei 1-uri și puteți face două perechi lipite, cu 1 corespunzător termenului X y , este folosit de două ori. În expresia funcției minime, trebuie să scrieți termenii perechilor care sunt lipite, lăsând în ele toate variabilele care nu se schimbă pentru această pereche și eliminând variabilele care își schimbă valoarea. Pentru lipirea orizontală obținem X , iar pentru verticală y , ca rezultat obținem expresia
f = x + y.
În fig. 9 arată tabelele de adevăr a două funcții a trei variabile ( A ) și hărțile lor Carnot ( b și c). Funcția f 2 diferă de prima prin faptul că nu este definită pe trei seturi de variabile (în tabel aceasta este indicată printr-o liniuță).
La determinarea funcției DNF minime, se folosesc următoarele reguli. Toate celulele care conțin 1 sunt combinate în zone dreptunghiulare închise numite k-cuburi, unde k = log 2 K, K cantitatea 1 într-o zonă dreptunghiulară. În acest caz, fiecare zonă ar trebui să fie un dreptunghi cu numărul de celule 2 k, unde k = 0, 1, 2, 3, …. Pentru k = Se numeste 1 dreptunghi unul este un cub și conține 2 1 = 2 unități; pentru k = 2 dreptunghi conține 2 2 = 4 unități și se numește două cuburi; pentru k = 3 regiunea lui 2 3 = 8 unități se numesc trei cuburi ; etc. Pot fi numite unități care nu pot fi combinate în dreptunghiuri zero-cuburi , care conțin o singură unitate (2 0 = 1). După cum se vede, chiar și k zonele pot avea o formă pătrată (dar nu neapărat) și dacă sunt impare k numai dreptunghiuri.
|
b c |
||||||
Orez. 9. Exemplu de hărți Karnaugh pentru funcții a trei variabile
Aceste regiuni se pot suprapune, adică aceleași celule pot intra în regiuni diferite. Atunci funcția DNF minimă este scrisă ca disjuncția tuturor termenilor conjunctivi corespunzători k - cuburi.
Fiecare dintre zonele indicate pe harta Karnaugh este reprezentată într-un DNF minim printr-o conjuncție, numărul de argumente în care este k mai mic decât numărul total de argumente ale funcției m , adică acest număr este egal mk . Fiecare conjuncție a unui DNF minim este compusă numai din acele argumente care pentru zona corespunzătoare a hărții au valori fie fără inversiuni, fie numai cu inversiuni, adică nu își schimbă sensul.
Astfel, atunci când acoperiți celulele hărții cu zone închise, trebuie să ne străduim să vă asigurați că numărul de zone este minim și fiecare zonă conține cât mai multe celule posibil, deoarece în acest caz numărul de termeni din DNF minim va fi minim și numărul de argumente în conjuncția corespunzătoare va fi minim.
Pentru funcția conform hărții Karnaugh din Fig. 9, b găsim
întrucât pentru regiunea închisă superioară variabilele x 1 și x 2 au valori fara inversiuni, pentru cele mai mici x 1 contează cu inversiunea și x 3 fără inversare.
Valori nedefinite în harta din Fig. 9, V poate fi definit în continuare prin înlocuirea acestuia cu zero sau unu. Pentru această funcție, este clar că este mai profitabil să înlocuiți ambele valori nedefinite cu 1. În acest caz, se formează două zone, care sunt tipuri diferite de 2-cuburi. Atunci expresia pentru funcția DNF minimă va fi următoarea:
Când construiți zone închise, este permisă plierea hărții Carnaugh într-un cilindru atât pe orizontală, cât și pe verticală. R axele tikal cu unirea fețelor opuse R tu, adică unități situate de-a lungul marginilor hărții de simetrie Carnot h dar poate fi și combinat.
Hărțile Carnaugh pot fi desenate în diferite moduri (Fig. 10).
|
x 2 x 3 |
||||||||||
a b
Orez. 10. Diferite moduri de a descrie hărțile Carnaugh
pentru o funcție de 3 variabile
Dar cele mai convenabile opțiuni pentru hărțile Karnaugh pentru funcții de 2-4 variabile sunt cele prezentate în Fig. 11 tabele, pentru că arată pentru fiecare celulă A Avem toate variabilele în formă directă sau inversă.
a b
Orez. unsprezece. Cea mai convenabilă imagine a hărților Carnaugh
pentru funcțiile 3 ( a) și 4 (b) variabile
Pentru funcțiile cu 5 și 6 variabile, metoda prezentată în Fig. 10, V .
Orez. 12. Imagine a unei hărți Karnaugh pentru o funcție de 5 variabile
Orez. 13. Imagine a unei hărți Karnaugh pentru o funcție de 6 variabile
Alte lucrări similare care vă pot interesa.vshm> |
|||
| 9020. | PRINCIPIUL DUALITĂȚII. EXTENSIREA FUNCȚIILOR BOOLEANE ÎN VARIABILE. FORME NORMALE DISJUNCTIVE ȘI CONJUNCTIVE PERFECTE | 96,34 KB | |
| Această teoremă este de natură constructivă, deoarece permite fiecărei funcție să construiască o formulă care o implementează sub forma unui d.n perfect. f. Pentru a face acest lucru, în tabelul de adevăr pentru fiecare funcție, marchem toate rândurile în care | |||
| 6490. | Descrierea și minimizarea funcțiilor logice | 187,21 KB | |
| Relația dintre argumentele unei funcții și valorile acesteia este exprimată în formă verbală. Exemplu: O funcție cu trei argumente ia o valoare atunci când oricare două sau mai multe argumente ale funcției sunt egale. Constă în construirea unui tabel de adevăr care conține valorile funcției pentru toate seturile de valori ale argumentelor. În acest exemplu, folosind tabelul de adevăr, obținem următoarea intrare sub formă de DNF... | |||
| 6707. | Proiectarea bazelor de date relaționale. Probleme de proiectare în abordarea clasică. Principii de normalizare, forme normale | 70,48 KB | |
| Ce este un proiect de baze de date relaționale Acesta este un set de relații interconectate în care sunt definite toate atributele, sunt specificate cheile primare ale relațiilor și sunt specificate unele proprietăți suplimentare ale relațiilor care se referă la principiile menținerii integrității. Prin urmare, proiectarea bazei de date trebuie să fie foarte precisă și verificată. De fapt, un proiect de bază de date stă la baza unui viitor pachet software care va fi folosit destul de mult timp și de mulți utilizatori. | |||
| 4849. | Forme și metode de implementare a funcțiilor de stat | 197,3 KB | |
| Termenul „funcție” are departe de a fi același înțeles în literatura științifică națională și străină. În termeni filosofici și sociologici generali, este considerată ca „o manifestare externă a proprietăților unui obiect într-un sistem dat de relații”; ca un ansamblu de acţiuni obişnuite sau specifice ale indivizilor sau organismelor | |||
| 17873. | Formarea UUD logic pentru elevii clasei a III-a | 846,71 KB | |
| Aspecte psihologice și pedagogice ale problemei formării acțiunilor logice universale la elevii din ciclul primar Metode de evaluare a formării UUD-urilor logice. Elaborarea unui concept pentru dezvoltarea activităților educaționale universale în sistemul de învățământ general răspunde noilor nevoi sociale. Cea mai importantă sarcină a sistemului modern de învățământ este formarea activităților educaționale universale ale UUD. Formarea de activități educaționale universale este cheia prevenirii dificultăților școlare. | |||
| 2638. | Implementarea tehnică a conexiunilor logice în sistemele automate de blocare | 1,04 MB | |
| Implementarea tehnică a conexiunilor logice în sistemele de blocare automată Implementarea tehnică a algoritmilor de control pentru bateriile cu trei și patru cifre poate fi realizată utilizând contact rele și elemente logice discrete și integrale fără contact... | |||
| 10203. | APLICAREA CONCEPTULUI DE ABORDARE ORIENTATĂ LA RISC PENTRU CONSTRUIREA MODELELOR STRUCTURALE ȘI LOGICE DE Apariție ȘI DEZVOLTARE A URGENȚEI | 70,8 KB | |
| Analiza generală a riscurilor Mediul de producție devine saturat de sisteme tehnologice și tehnologii puternice care fac ca munca umană să fie productivă și mai puțin dificilă din punct de vedere fizic, dar mai periculoasă. Riscul se caracterizează prin caracterul neașteptat și brusc al apariției unei situații periculoase. În fiecare zi ne confruntăm cu numeroase riscuri, dar cele mai multe dintre ele rămân potențiale.Teoria riscului prevede o evaluare cantitativă a impactului negativ asupra unei persoane, precum și a prejudiciului asupra sănătății și vieții sale. | |||
| 11576. | Concept, tipuri și forme de tranzacții. Consecințele nerespectării formei cerute de tranzacții | 49,82 KB | |
| Recunoașterea unei tranzacții ca fiind nevalidă; tipuri de tranzacții nevalide. Valoarea aplicată a cursului constă în simplificarea conceptului de tranzacție, adică prezentarea publică a acesteia într-o formă mai accesibilă. | |||
| 6213. | Aproximarea funcției | 3,08 MB | |
| Prima constă în înlocuirea unei anumite funcții specificate analitic sau tabelar cu o altă funcție apropiată de cea inițială dar mai simplă și mai convenabilă pentru calcule. De exemplu, înlocuirea unei funcții cu un polinom vă permite să obțineți formule simple de integrare și diferențiere numerică; Înlocuirea tabelului cu o funcție de aproximare vă permite să obțineți valori în punctele sale intermediare. Apare și a doua problemă: restabilirea unei funcții pe un anumit segment din valorile funcției date pe acest segment într-un set discret de puncte. Raspunsul la aceasta intrebare... | |||
| 14058. | Evoluţia funcţiilor statului | 29,99 KB | |
| Statul rus, ca fenomen juridic, trebuie să asigure în primul rând punerea în aplicare a scopului statului, precum și a principalelor sale caracteristici constituționale ca stat laic social, federal, democratic, cu o formă republicană de guvernare. Scopul principal al statului este determinat de art. | |||
Exemplu. Găsiți formule CNF ![]()
~ ![]() ~
~
![]()
Forma normală disjunctivă perfectă a SDNF poate fi construită folosind următorul algoritm:
1. = 1. Algoritmul DNF
2. = 2. Algoritmul DNF
3. = 3. Algoritmul DNF
4. = 4. Algoritmul DNF
5. Omiteți termeni identic falși, adică termenii formei
6. Completați termenii rămași cu variabilele lipsă
7. Repetați punctul 4.
Exemplu. Găsiți formule SDNF.
![]() ~
~
![]()
![]()
![]()
![]()
Pentru a construi SCNF, puteți utiliza următoarea schemă:
Exemplu. Găsiți formule SDNF.
![]() ~
~
![]()
Este cunoscut (Teoremele 2.11, 2.12) că SDNF și SCNF sunt definite în mod unic prin formulă și, prin urmare, pot fi construite folosind tabelul de adevăr al formulei.
Schema de construire a SDNF și SCNF conform tabelului de adevăr este dată mai jos, pentru formula ![]() ~ :
~ :
| | ||||
| 1 0 1 0 1 1 0 1 | SDNF; SKNF. |
2.2. Exercițiu.
2.2.1 Mai jos sunt expresiile booleene. Simplificați expresiile variantei dvs. cât mai mult posibil folosind legile logicii lui Boole. Apoi utilizați tabelele de adevăr pentru a compara expresia simplificată cu cea originală.






2.2.2. Clarificați întrebarea echivalenței lui f 1 și f 2 reducându-le la SDNF (Tabelul 1).
2.2.3. Găsiți funcția duală pentru f 3 folosind principiul generalizat și boolean (Tabelul 1). Comparați rezultatele.
| № | f 1 | f 2 | f 3 |
| | |||
| |
|||
| | |||
| | |||
| | |||
| | |
||
| | |
||
| |
|||
| | |||
| | |||
| |
|||
| | |||
| | |
||
| | |||
| |
2.3. Întrebări de control.
2.3.1. Definiți o declarație.
2.3.2. Enumerați principalele operațiuni dintr-o declarație.
2.3.3. Ce este un tabel de adevăr?
2.3.4. Creați tabele de adevăr pentru următoarele formule:
~ ~ ![]() ~ ;
~ ;
2.3.5. Ținând cont de convențiile privind ordinea operațiilor, omiteți parantezele „extra” și semnul „ ” în formule:
![]() ;
;
2.3.6. Folosind transformări echivalente, dovediți adevărul identic al formulelor:
2.3.7. Găsiți formule duale:
![]()
![]()
![]() )
)
2.3.8. Reduceți următoarele formule la forma perfectă DNF (SDNF):
![]() ~
~
2.3.9. Reduceți următoarele formule la forma CNF perfectă (SCNF):
![]()
![]() ~
~
![]()
![]()
Lucrare de laborator nr 3
Subiect:„Minimizarea funcțiilor booleene. Logică"
Ţintă: Dobândirea abilităților practice în lucrul cu metode de minimizare a funcțiilor booleene.
3.1. Informații teoretice.
Forme minime
După cum sa arătat în, orice funcție booleană poate fi reprezentată în formă normală perfectă (disjunctivă sau conjunctivă). Mai mult decât atât, o astfel de reprezentare este primul pas în trecerea de la o specificație tabelară a unei funcții la expresia ei analitică. În cele ce urmează, vom proceda de la forma disjunctivă, iar rezultatele corespunzătoare pentru forma conjunctivă se obțin pe baza principiului dualității.
Problema canonică a sintetizării circuitelor logice pe o bază booleană se rezumă la minimizarea funcțiilor booleene, i.e. la reprezentarea lor în formă normală disjunctivă, care conține cel mai mic număr de litere (variabile și negațiile lor). Astfel de forme sunt numite minimale. În sinteza canonică, se presupune că atât semnalele, cât și inversiunile lor sunt furnizate la intrările circuitului.
Formula prezentată în formă normală disjunctivă este simplificată prin utilizarea repetată a operației de lipire și a operației de absorbție și (identitățile duale pentru forma normală conjunctivă au forma: și ). Aici, și poate fi înțeles ca orice formulă de algebră booleană. Ca urmare, ajungem la o expresie analitică în care transformările ulterioare nu mai sunt posibile, adică. obținem o formă fără fund.
Printre formele de fund există și o formă disjunctivă minimă și poate să nu fie unică. Pentru a vă asigura că o anumită formă de blocare este minimă, trebuie să găsiți toate formele de fund și să le comparați după numărul de litere pe care le conțin.
Să fie, de exemplu, funcția dată în formă disjunctivă normală perfectă:
Grupând termenii și aplicând operația de lipire, avem .
Cu o altă metodă de grupare obținem:
Ambele forme de fund nu sunt minime. Pentru a obține forma minimă, trebuie să ghiciți să repetați un termen din formula originală (acest lucru se poate face întotdeauna, deoarece ). În primul caz, un astfel de membru poate fi . Apoi . Adăugând termenul , obținem: . După ce ați trecut prin toate opțiunile posibile, vă puteți asigura că ultimele două forme sunt minime.
Lucrul cu formule la acest nivel este ca și cum ai rătăci în întuneric. Procesul de căutare a formelor minimale devine mai vizual și mai intenționat dacă folosiți unele reprezentări și simboluri grafice și analitice special dezvoltate în acest scop.
Cub multidimensional
Fiecare vârf al unui cub -dimensional poate fi asociat cu un constituent al unei unități. În consecință, submulțimea vârfurilor marcate este o mapare pe cubul -dimensional al unei funcții booleene de variabile în formă normală disjunctivă perfectă. În fig. 3.1 prezintă o astfel de mapare pentru funcția din clauza 3.7.

Fig. 3.1 Afișarea unei funcții prezentate în SDNF pe un cub tridimensional
Pentru a afișa o funcție de variabile prezentate în orice formă normală disjunctivă, este necesar să se stabilească o corespondență între minitermenii acesteia și elementele cubului -dimensional.
Un minitermen de rang (-1) poate fi considerat ca rezultat al lipirii a doi minitermen de rang (constituent al unității), i.e. ![]() , Pe un cub -dimensional, aceasta corespunde înlocuirii a două vârfuri care diferă doar prin valorile coordonatei care leagă aceste vârfuri cu o muchie (se spune că muchia acoperă vârfurile incidente cu aceasta). Astfel, minitermenii de ordinul (-1) corespund muchiilor cubului -dimensional. În mod similar, corespondența minitermenilor de ordinul (-2) se stabilește cu fețele unui cub -dimensional, fiecare dintre ele acoperă patru vârfuri (și patru muchii).
, Pe un cub -dimensional, aceasta corespunde înlocuirii a două vârfuri care diferă doar prin valorile coordonatei care leagă aceste vârfuri cu o muchie (se spune că muchia acoperă vârfurile incidente cu aceasta). Astfel, minitermenii de ordinul (-1) corespund muchiilor cubului -dimensional. În mod similar, corespondența minitermenilor de ordinul (-2) se stabilește cu fețele unui cub -dimensional, fiecare dintre ele acoperă patru vârfuri (și patru muchii).
Elementele unui cub -dimensional caracterizate prin dimensiuni se numesc -cuburi. Astfel, vârfurile sunt 0-cuburi, muchiile sunt 1-cuburi, fețele sunt 2-cuburi etc. Generalizând raționamentul de mai sus, putem presupune că un minitermen de ()-al-lea rang în formă normală disjunctivă pentru o funcție de variabile este reprezentat de un -cub, iar fiecare -cub acoperă toate acele -cuburi de dimensiune inferioară care sunt asociate cu vârfuri. Ca exemplu în Fig. 3.2 prezintă o funcție a trei variabile. Aici minitermenii corespund cu 1-cub (), iar minitermenul este reprezentat de un 2-cub ().

Fig.3.2 Acoperirea funcției ![]()
Deci, orice formă normală disjunctivă este mapată pe un cub -dimensional printr-un set de -cuburi care acoperă toate vârfurile corespunzătoare constituenților unității (0-cuburi). Afirmația inversă este, de asemenea, adevărată: dacă un anumit set de -cuburi acoperă mulțimea tuturor nodurilor corespunzătoare valorilor unitare ale unei funcții, atunci disjuncția minitermenilor corespunzătoare acestor -cuburi este o expresie a acestei funcții în normal disjunctiv. formă. Se spune că o astfel de colecție de -cuburi (sau minitermenii lor corespunzători) formează o acoperire a unei funcții.
Dorința unei forme minimale este înțeleasă intuitiv ca o căutare a unei astfel de acoperiri, al cărui număr de cuburi ar fi mai mic, iar dimensiunea lor ar fi mai mare. Acoperirea corespunzătoare formei minime se numește acoperire minimă. De exemplu, pentru funcția de acoperire din Fig. 3.3 îndeplinește formele minime ![]() Și
Și ![]() .
.

Orez. 3.3 Acoperiri de funcții.
stânga – ![]() ; pe dreapta –
; pe dreapta – ![]()
 Afișarea unei funcții pe un cub -dimensional este clară și simplă atunci când . Un cub cu patru dimensiuni poate fi reprezentat așa cum se arată în Fig. 3.4, care arată o funcție a patru variabile și acoperirea minimă a acesteia corespunzătoare expresiei
Afișarea unei funcții pe un cub -dimensional este clară și simplă atunci când . Un cub cu patru dimensiuni poate fi reprezentat așa cum se arată în Fig. 3.4, care arată o funcție a patru variabile și acoperirea minimă a acesteia corespunzătoare expresiei ![]() . Folosirea acestei metode necesită construcții atât de complexe încât toate avantajele sale se pierd.
. Folosirea acestei metode necesită construcții atât de complexe încât toate avantajele sale se pierd.
Orez. 3.4 Afișaj funcțional ![]() pe un cub cu patru dimensiuni
pe un cub cu patru dimensiuni
Hărți Carnot
O altă metodă pentru afișarea grafică a funcțiilor booleene folosește Hărți Carnot, care sunt tabele de corespondență special organizate. Coloanele și rândurile tabelului corespund tuturor seturilor posibile de valori a nu mai mult de două variabile, iar aceste seturi sunt aranjate într-o astfel de ordine încât fiecare dintre cele ulterioare diferă de precedentul prin valoarea uneia dintre variabile. . Datorită acestui fapt, celulele învecinate ale tabelului diferă pe orizontală și pe verticală prin valoarea unei singure variabile. Celulele situate la marginile tabelului sunt, de asemenea, considerate adiacente și au această proprietate. În fig. Figura 3.5 prezintă hărți Karnaugh pentru două, trei, patru variabile.
 |
|||||
 |
|||||
 |
|||||
Orez. 3.5 Hărți Carnaugh pentru două, trei și patru variabile
Ca și în tabelele de adevăr obișnuite, celulele mulțimilor în care funcția ia valoarea 1 sunt umplute cu unu (zerourile de obicei nu se potrivesc, ele corespund celulelor goale). De exemplu, în Fig. 3.6, A arată o hartă Karnaugh pentru o funcție, a cărei afișare pe un cub cu patru dimensiuni este dată în Fig. 3.4. Pentru a simplifica lucrurile, rândurile și coloanele corespunzătoare valorilor de 1 pentru o variabilă sunt evidențiate cu o acoladă care indică acea variabilă.
 |
|||
 |
|||
Orez. 3.6 Afișarea unei funcții a patru variabile pe o hartă Carnaugh
(a) și acoperirea minimă a acesteia (b)
Între mapările funcțiilor la n-cubul dimensional și harta Carnot există o corespondență unu-la-unu. Pe harta Carnot s-un cub corespunde unui set de 2 celule invecinate asezate intr-un rand, coloana, patrat sau dreptunghi (tinand cont de apropierea marginilor opuse ale hartii). Prin urmare, toate prevederile expuse mai sus (a se vedea paragraful. cub multidimensional), sunt valabile pentru hărțile Karnaugh. Deci, în fig. 3.6, b arată acoperirea unităților hărții corespunzătoare formei disjunctive minime ![]() funcția în cauză.
funcția în cauză.
Citirea termenilor de pe o hartă Karnaugh urmează o regulă simplă. Se formează celule s-cub, da miniter (n–s)- rangul, care le include pe acelea (n–s) variabile care păstrează aceleași valori pe aceasta s-cub, unde valoarea 1 corespunde variabilelor în sine, iar valoarea 0 corespunde negațiilor acestora. Variabile care nu își păstrează valorile pentru s-cub, sunt absente în miniterm. Diferite moduri de citire au ca rezultat reprezentări diferite ale funcției în formă normală disjunctivă (cea din extrema dreaptă este minimă) (Figura 3.7).
 |  |
||||||||
 |
|||||||||
Utilizarea hărților Karnaugh necesită construcții mai simple în comparație cu cartografierea n-cub dimensional, mai ales în cazul a patru variabile. Pentru a afișa funcții a cinci variabile, sunt utilizate două hărți Karnaugh pentru patru variabile, iar pentru o funcție de șase variabile sunt folosite patru astfel de hărți. Odată cu o creștere suplimentară a numărului de variabile, hărțile Karnaugh devin practic inutilizabile.
Celebru în literatură Carduri Veitch Ele diferă doar în ordinea diferită a seturilor de valori variabile și au aceleași proprietăți ca hărțile Karnaugh.
Complex de cuburi
Inconsecvența metodelor grafice cu un număr mare de variabile este compensată de diverse metode analitice de reprezentare a funcțiilor booleene. O astfel de reprezentare este complex de cuburi, folosind terminologia unui spațiu logic multidimensional în combinație cu simbolismul special dezvoltat.
). 0-cuburile corespunzătoare constituenților unității sunt reprezentate prin seturi de valori variabile pe care funcția este egală cu unitatea. Evident, în înregistrare


Orez. 3.8 Complex de cuburi ale unei funcții de trei variabile ( A) și reprezentarea sa simbolică ( b)
Se formează complexul de cuburi acoperire maximă a funcției. Excluzând din el pe toți cei s-cuburi care sunt acoperite de cuburi de dimensiune superioara, obtinem acoperiri corespunzatoare formelor de fund. Deci, pentru exemplul luat în considerare (Fig. 3.8) avem o acoperire fără fund
 ,
,
care corespunde funcţiei ![]() . În acest caz, această acoperire este minimă.
. În acest caz, această acoperire este minimă.
Pentru două funcții booleene, operația de disjuncție corespunde unirii complexelor lor de cuburi, iar operația de conjuncție corespunde intersecției complexelor lor de cuburi. Negația unei funcții corespunde complementului unui complex de cuburi, adică și este determinată de toate vârfurile la care funcția ia valoarea 0. Astfel, există o corespondență unu-la-unu (izomorfism) între algebra lui Funcții booleene și mulțimi booleene reprezentând complexe de cuburi.
Reprezentarea unei funcții sub formă de complexe de cuburi este mai puțin vizuală, dar cele mai importante avantaje ale acesteia sunt că restricțiile privind numărul de variabile sunt eliminate și codificarea informațiilor este facilitată atunci când se utilizează computere.
Minimizarea funcțiilor booleene
Formularea problemei. Minimizarea unui circuit pe o bază booleană se reduce la găsirea formei disjunctive minime care corespunde acoperirii minime. Numărul total de litere incluse în forma normală este exprimat prin costul acoperirii ![]() , unde este numărul de cuburi care formează acoperirea unei funcții date de n variabile. Acoperirea minimă este caracterizată de cea mai mică valoare a prețului său.
, unde este numărul de cuburi care formează acoperirea unei funcții date de n variabile. Acoperirea minimă este caracterizată de cea mai mică valoare a prețului său.
De obicei, problema minimizării este rezolvată în doi pași. În primul rând, căutăm o husă redusă care să includă toate -cuburile de dimensiune maximă, dar să nu conțină un singur cub acoperit de niciun cub din această husă. Forma normală disjunctivă corespunzătoare se numește redusă, iar minitermenii ei sunt numiți implicanți simpli. Pentru o anumită funcție, acoperirea redusă este unică, dar poate fi redundantă datorită faptului că unele dintre cuburi sunt acoperite de colecții de alte cuburi.
La a doua etapă, se face o tranziție de la formele normale disjunctive reduse la forme normale disjunctive, din care sunt selectate formele minime. Formele de fund se formează prin excluderea din acoperirea redusă a tuturor cuburilor redundante, fără de care setul de cuburi rămas încă formează o acoperire a unei anumite funcții, dar cu excluderea suplimentară a oricăruia dintre cuburi, nu mai acoperă setul tuturor vârfuri corespunzătoare unor valori individuale ale funcției, adică încetează să mai fie o acoperire.
Un cub de acoperire redusă care acoperă vârfuri ale unei anumite funcții care nu sunt acoperite de niciun alt cub nu poate fi redundant și va fi întotdeauna inclus în acoperirea minimă. Un astfel de cub, la fel ca implicantul său corespondent, se numește extremal (implicant esențial), iar vârfurile pe care le acoperă sunt numite vârfuri anulate. Setul de extremale formează miezul învelișului; este clar că atunci când se trece de la o acoperire redusă la una minimă, în primul rând, toate extremele trebuie izolate. Dacă setul de extremale nu formează o acoperire, atunci se completează pentru a se acoperi cu cuburi din învelișul redus.
Definițiile date sunt ilustrate în Fig. 3.9, unde acoperirea redusă (vezi Fig. 3.9a, ) iar acoperirile minime (Fig. 3.9b) și (vezi Fig. 3.9, b) sunt exprimate după cum urmează.