Integrale ale funcțiilor trigonometrice. Exemple de soluții. Integrarea funcțiilor trigonometrice Antiderivată a tangentei x

Integrale ale funcțiilor trigonometrice.
Exemple de soluții

În această lecție ne vom uita la integralele funcțiilor trigonometrice, adică umplerea integralelor va fi sinusuri, cosinus, tangente și cotangente în diverse combinații. Toate exemplele vor fi analizate în detaliu, accesibile și de înțeles chiar și pentru un ceainic.

Pentru a studia cu succes integralele funcțiilor trigonometrice, trebuie să aveți o bună înțelegere a celor mai simple integrale, precum și să stăpâniți câteva tehnici de integrare. Vă puteți familiariza cu aceste materiale în cadrul prelegerilor Integrală nedefinită. Exemple de soluțiiȘi .

Și acum avem nevoie de: Tabelul integralelor, Tabelul derivatelorȘi Director de formule trigonometrice. Toate materialele didactice pot fi găsite pe pagină Formule și tabele matematice. Recomand să imprimați totul. Mă concentrez în special pe formulele trigonometrice, ar trebui să fie în fața ochilor tăi– fără aceasta, eficiența muncii va scădea vizibil.

Dar mai întâi, despre ce sunt integralele în acest articol Nu. Nu există integrale ale formei, - cosinus, sinus, înmulțit cu vreun polinom (mai rar ceva cu tangentă sau cotangentă). Astfel de integrale sunt integrate pe părți, iar pentru a învăța metoda, vizitați lecția Integrare pe părți. Exemple de soluții De asemenea, aici nu există integrale cu „arcuri” - arctangente, arcsinus etc., de asemenea, ele sunt de cele mai multe ori integrate prin părți.

Când se găsesc integrale ale funcțiilor trigonometrice, se utilizează o serie de metode:

(4) Folosim formula tabelară , singura diferență este că în loc de „X” avem o expresie complexă.

Exemplul 2

Exemplul 3

Aflați integrala nedefinită.

Un clasic al genului pentru cei care se îneacă în competiție. După cum probabil ați observat, în tabelul de integrale nu există nicio integrală a tangentei și cotangentei, dar, cu toate acestea, astfel de integrale pot fi găsite.

(1) Folosim formula trigonometrică

(2) Aducem funcția sub semnul diferențial.

(3) Folosim integrala tabelului .

Exemplul 4

Aflați integrala nedefinită.

Acesta este un exemplu pentru o soluție independentă, soluția completă și răspunsul sunt la sfârșitul lecției.

Exemplul 5

Aflați integrala nedefinită.

Gradele noastre vor crește treptat =).
In primul rand solutia:

(1) Folosim formula

(2) Folosim identitatea trigonometrică principală , din care rezultă că .

(3) Împărțiți numărătorul la numitor termen cu termen.

(4) Folosim proprietatea de liniaritate a integralei nedefinite.

(5) Integram folosind tabelul.

Exemplul 6

Aflați integrala nedefinită.

Acesta este un exemplu pentru o soluție independentă, soluția completă și răspunsul sunt la sfârșitul lecției.

Există, de asemenea, integrale de tangente și cotangente, care sunt în puteri mai mari. Integrala tangentei cube este discutată în lecție Cum se calculează aria unei figuri plate? Integrale de tangentă (cotangente) la a patra și a cincea puteri pot fi obținute pe pagină Integrale complexe.

Reducerea gradului de integrand

Această tehnică funcționează atunci când funcțiile integrand sunt umplute cu sinusuri și cosinusuri chiar grade. Pentru a reduce gradul, utilizați formule trigonometrice , și , iar ultima formulă este adesea folosită în direcția opusă: .

Exemplul 7

Aflați integrala nedefinită.

Soluţie:

În principiu, nu este nimic nou aici, decât că am aplicat formula (scăderea gradului de integrand). Vă rugăm să rețineți că am scurtat soluția. Pe măsură ce câștigați experiență, integrala poate fi găsită pe cale orală, acest lucru economisește timp și este destul de acceptabil la terminarea sarcinilor. În acest caz, este recomandabil să nu descrieți regula , mai întâi luăm verbal integrala lui 1, apoi a lui .

Exemplul 8

Aflați integrala nedefinită.

Acesta este un exemplu pentru o soluție independentă, soluția completă și răspunsul sunt la sfârșitul lecției.

Aceasta este creșterea de grad promisă:

Exemplul 9

Aflați integrala nedefinită.

Mai intai solutia, apoi comentariile:

(1) Pregătiți integrantul pentru a aplica formula .

(2) Aplicam de fapt formula.

(3) Pătratăm numitorul și scoatem constanta din semnul integral. Ar fi putut fi făcut puțin diferit, dar, după părerea mea, a fost mai convenabil.

(4) Folosim formula

(5) În al treilea termen reducem din nou gradul, dar folosind formula .

(6) Prezentăm termeni similari (aici am împărțit termen cu termen și a făcut adăugarea).

(7) De fapt, luăm integrala, regula liniarității iar metoda de subsumare a unei funcţii sub semnul diferenţial se realizează oral.

(8) Pieptănarea răspunsului.

! Într-o integrală nedefinită, răspunsul poate fi adesea scris în mai multe moduri

În exemplul luat în considerare, răspunsul final ar fi putut fi scris diferit - deschizând parantezele și chiar făcând acest lucru înainte de a integra expresia, adică următorul sfârșit al exemplului este destul de acceptabil:

Este foarte posibil ca această opțiune să fie și mai convenabilă, tocmai am explicat-o așa cum obișnuiesc să o rezolv eu). Iată un alt exemplu tipic pentru o soluție independentă:

Exemplul 10

Aflați integrala nedefinită.

Acest exemplu poate fi rezolvat în două moduri și s-ar putea să reușiți două răspunsuri complet diferite(mai precis, vor arăta cu totul diferit, dar din punct de vedere matematic vor fi echivalente). Cel mai probabil, nu vei vedea cea mai rațională metodă și vei avea de suferit cu deschiderea parantezelor și folosind alte formule trigonometrice. Cea mai eficientă soluție este dată la sfârșitul lecției.

Pentru a rezuma paragraful, concluzionăm: orice integrală a formei , unde și – chiar numere, se rezolvă prin metoda reducerii gradului integrandului.
În practică, am dat peste integrale cu 8 și 10 grade și a trebuit să rezolv mizeria lor groaznică coborând gradul de mai multe ori, rezultând răspunsuri lungi, lungi.

Metoda de înlocuire a variabilei

După cum se menționează în articol Metoda modificării variabilei în integrală nedefinită, principala condiție pentru utilizarea metodei de înlocuire este faptul că în integrand există o anumită funcție și derivata ei:
(funcțiile nu sunt neapărat în produs)

Exemplul 11

Aflați integrala nedefinită.

Ne uităm la tabelul derivatelor și observăm formulele, , adică în integrandul nostru există o funcție și derivata ei. Cu toate acestea, vedem că în timpul diferențierii, cosinusul și sinusul se transformă reciproc unul în celălalt și se pune întrebarea: cum se efectuează o schimbare de variabilă și ce înțelegem prin sinus sau cosinus?! Întrebarea poate fi rezolvată prin înțepături științifice: dacă înlocuim incorect, atunci nu va ieși nimic bun.

Un ghid general: în cazuri similare, trebuie să desemnați funcția care se află în numitor.

Întrerupem soluția și facem o înlocuire

Totul este bine la numitor, totul depinde doar de , acum rămâne de aflat în ce se va transforma.
Pentru a face acest lucru, găsim diferența:

Sau, pe scurt:
Din egalitatea rezultată, folosind regula proporției, exprimăm expresia de care avem nevoie:

Asa de:

Acum întregul nostru integrand depinde doar de și putem continua să rezolvăm

Gata. Permiteți-mi să vă reamintesc că scopul înlocuirii este de a simplifica integrand în acest caz, totul s-a rezumat la integrarea funcției de putere conform tabelului;

Nu este o coincidență că am descris acest exemplu atât de detaliat, acest lucru a fost făcut în scopul de a repeta și întări materialele de lecție Metoda modificării variabilei în integrală nedefinită.

Și acum două exemple pentru propria ta soluție:

Exemplul 12

Aflați integrala nedefinită.

Exemplul 13

Aflați integrala nedefinită.

Soluții și răspunsuri complete la sfârșitul lecției.

Exemplul 14

Aflați integrala nedefinită.

Din nou, în integrand, există sinus și cosinus (o funcție cu derivată), dar într-un produs și apare o dilemă - ce înțelegem prin sinus sau cosinus?

Puteți încerca să efectuați o înlocuire folosind metoda științifică și, dacă nimic nu funcționează, atunci desemnați-o ca altă funcție, dar există:

Orientare generală: trebuie să desemnați funcția care, la figurat vorbind, se află într-o „poziție incomodă”.

Vedem că în acest exemplu cosinusul studentului „sufă” de la grad, iar sinusul stă liber, de unul singur.

Prin urmare, să facem o înlocuire:

Dacă cineva mai are dificultăți cu algoritmul pentru înlocuirea unei variabile și găsirea diferenţialului, atunci ar trebui să revii la lecție Metoda modificării variabilei în integrală nedefinită.

Exemplul 15

Aflați integrala nedefinită.

Să analizăm integrandul, ce ar trebui notat cu ?
Să ne amintim regulile noastre:
1) Funcția este cel mai probabil la numitor;
2) Funcția este într-o „poziție incomodă”.

Apropo, aceste linii directoare sunt valabile nu numai pentru funcțiile trigonometrice.

Sinusul se potrivește ambelor criterii (în special al doilea), așa că se sugerează un înlocuitor. În principiu, înlocuirea poate fi deja efectuată, dar mai întâi ar fi bine să ne dăm seama cu ce să faceți? În primul rând, „prindem” un cosinus:

Ne rezervăm pentru diferența noastră „viitoare”.

Și o exprimăm prin sinus folosind identitatea trigonometrică de bază:

Acum iată înlocuitorul:

Regula generala: Daca in integrand una dintre functiile trigonometrice (sinus sau cosinus) este in ciudat grad, atunci trebuie să „mușcăți” o funcție din gradul impar și să desemnați o altă funcție în spatele acesteia. Vorbim doar de integrale unde există cosinus și sinusuri.

În exemplul luat în considerare, am avut un cosinus la o putere impară, așa că am scos un cosinus din putere și l-am desemnat ca sinus.

Exemplul 16

Aflați integrala nedefinită.

Decolează grade =).
Acesta este un exemplu de rezolvat singur. Soluție completă și răspuns la sfârșitul lecției.

Substituție trigonometrică universală

Substituția trigonometrică universală este un caz comun al metodei de înlocuire a variabilei. Poți încerca să-l folosești atunci când „nu știi ce să faci”. Dar, de fapt, există câteva linii directoare pentru aplicarea acestuia. Integrale tipice în care trebuie aplicată substituția trigonometrică universală sunt următoarele integrale: , , , etc.

Exemplul 17

Aflați integrala nedefinită.

Substituția trigonometrică universală în acest caz este implementată în felul următor. Să înlocuim: . Nu folosesc litera , ci litera , aceasta nu este un fel de regulă, doar că, din nou, sunt obișnuit să rezolv lucrurile în acest fel.

Aici este mai convenabil să găsim diferența pentru aceasta, din egalitate, exprim:
Atașez un arctangent la ambele părți:

Arctangenta și tangenta se anulează reciproc:

Prin urmare:

În practică, nu trebuie să o descrieți atât de detaliat, ci pur și simplu să utilizați rezultatul final:

! Expresia este valabilă numai dacă sub sinusuri și cosinus avem pur și simplu „X”, pentru integrală (despre care vom vorbi mai târziu) totul va fi puțin diferit!

La înlocuire, sinusurile și cosinusurile se transformă în următoarele fracții:
, , aceste egalități se bazează pe formule trigonometrice binecunoscute: ,

Deci, designul final ar putea arăta astfel:

Să efectuăm o înlocuire trigonometrică universală:

Pentru a integra funcții raționale de forma R(sin x, cos x), se folosește o substituție, care se numește substituție trigonometrică universală. Apoi . Substituția trigonometrică universală duce adesea la calcule mari. Prin urmare, ori de câte ori este posibil, utilizați următoarele înlocuiri.

Integrarea funcţiilor dependente raţional de funcţiile trigonometrice

Să folosim formulele pentru conversia produsului funcțiilor trigonometrice în suma lor:

• sin α cos β = ½(sin(α+β)+sin(α-β))
• cos α cos β = ½(cos(α+β)+cos(α-β))
• sin α sin β = ½(cos(α-β)-cos(α+β))

Exemple
1. Calculați integrala ∫ cos 4 x·sin 3 xdx .
Facem înlocuirea cos(x)=t. Atunci ∫ cos 4 x sin 3 xdx =
2. Calculați integrala.
Făcând înlocuirea sin x=t , obținem

Integrarea expresiilor de forma R(sinx, cosx)

Exemplul nr. 1. Calculați integralele:

Soluţie.
a) Integrarea expresiilor de forma R(sinx, cosx), unde R este o funcție rațională a sin x și cos x, sunt convertite în integrale ale funcțiilor raționale folosind substituția trigonometrică universală tg(x/2) = t.
Atunci noi avem

• Dacă egalitatea R(-sin x, cos x) = -R(sin x, cos x)dx este satisfăcută, atunci se aplică substituția cos x = t.
• Dacă egalitatea R(sin x, -cos x) = -R(sin x, cos x)dx este valabilă, atunci substituția sin x = t.
• Dacă egalitatea R(-sin x, -cos x) = R(sin x, cos x)dx este valabilă, atunci substituția tgx = t sau ctg x = t.

Vor fi și probleme pe care să le rezolvați singur, la care puteți vedea răspunsurile.

Integrandul poate fi convertit din produsul funcțiilor trigonometrice în sumă

Să considerăm integralele în care integrandul este produsul dintre sinusuri și cosinusuri de gradul întâi al lui x înmulțit cu diferiți factori, adică integrale de forma

Folosind formule trigonometrice binecunoscute

(2)
(3)
(4)
se poate transforma fiecare dintre produsele în integrale de forma (31) într-o sumă algebrică și se integrează după formulele

(5)

(6)

Exemplul 1. Găsi

Soluţie. Conform formulei (2) la

Exemplul 2. Găsi integrală a unei funcții trigonometrice

Soluţie. Conform formulei (3) la

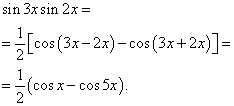
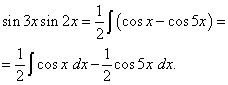
Exemplul 3. Găsi integrală a unei funcții trigonometrice

Soluţie. Conform formulei (4) la obținem următoarea transformare a integrandului:

Aplicând formula (6), obținem

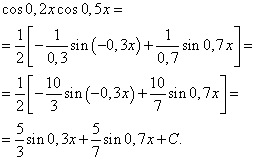
Integrală a produsului puterilor sinusului și cosinusului aceluiași argument

Să considerăm acum integralele funcțiilor care sunt produsul puterilor sinusului și cosinusului aceluiași argument, i.e.

(7)

În cazuri speciale, unul dintre indicatorii ( m sau n) poate fi zero.

La integrarea unor astfel de funcții, se folosește că o putere pară a cosinusului poate fi exprimată prin sinus, iar diferența sinusului este egală cu cos x dx(sau chiar puterea sinusului poate fi exprimată în termeni de cosinus, iar diferența de cosinus este egală cu - sin x dx ) .

Trebuie distinse două cazuri: 1) cel puțin unul dintre indicatori mȘi n ciudat; 2) ambii indicatori sunt egali.

Să aibă loc primul caz, și anume indicatorul n = 2k+ 1 - impar. Atunci, având în vedere că

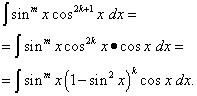
Integrandul este prezentat în așa fel încât o parte a acestuia este o funcție numai a sinusului, iar cealaltă este diferența de sinus. Acum se utilizează înlocuirea variabilă t= păcat X soluţia se reduce la integrarea polinomului faţă de t. Dacă numai gradul m este ciudat, atunci ei fac la fel, izolând factorul sin X, exprimând restul integrandului în termeni de cos Xși crezând t=cos X. Această tehnică poate fi folosită și când integrând puterile câte ale sinusului și cosinusului , Când cel puțin unul dintre indicatori este impar . Ideea este că câtul puterilor sinusului și cosinusului este un caz special al produsului lor : Când o funcție trigonometrică se află la numitorul unui integrand, gradul acesteia este negativ. Dar există și cazuri de funcții trigonometrice parțiale, când puterile lor sunt doar pare. Despre ei - în paragraful următor.

Dacă ambii indicatori mȘi n– chiar, atunci, folosind formule trigonometrice

reduceți exponenții sinusului și cosinusului, după care se obține o integrală de același tip ca mai sus. Prin urmare, integrarea ar trebui continuată conform aceleiași scheme. Dacă unul dintre exponenții pare este negativ, adică se ia în considerare câtul puterilor pare ale sinusului și cosinusului, atunci această schemă nu este potrivită . Apoi se folosește o schimbare de variabilă în funcție de modul în care poate fi transformat integrantul. Un astfel de caz va fi luat în considerare în paragraful următor.

Exemplul 4. Găsi integrală a unei funcții trigonometrice

Soluţie. Exponentul cosinus este impar. Prin urmare, să ne imaginăm

t= păcat X(Apoi dt=cos X dx ). Apoi primim

Revenind la vechea variabilă, găsim în sfârșit

Exemplul 5. Găsi integrală a unei funcții trigonometrice

.

Soluţie. Exponentul cosinus, ca în exemplul anterior, este impar, dar mai mare. Să ne imaginăm

și faceți o schimbare de variabilă t= păcat X(Apoi dt=cos X dx ). Apoi primim

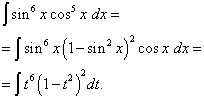
Să deschidem parantezele

și primim

Revenind la vechea variabilă, obținem soluția

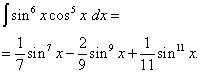
Exemplul 6. Găsi integrală a unei funcții trigonometrice

Soluţie. Exponenții sinusului și cosinusului sunt pari. Prin urmare, transformăm funcția integrand după cum urmează:

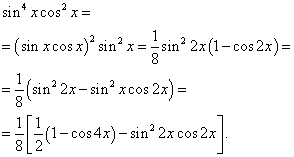
Apoi primim

În a doua integrală facem o schimbare de variabilă, setare t= sin2 X. Apoi (1/2)dt= cos2 X dx . Prin urmare,

În sfârșit, obținem

Folosind metoda de înlocuire a variabilelor

Metoda de înlocuire a variabilei la integrarea funcțiilor trigonometrice, poate fi utilizat în cazurile în care integrandul conține doar sinus sau numai cosinus, produsul dintre sinus și cosinus, în care fie sinus, fie cosinus este în gradul I, tangent sau cotangent, precum și câtul dintre chiar şi puteri de sinus şi cosinus ale unuia şi aceluiaşi argument. În acest caz, este posibil să se efectueze permutări nu numai păcat X = tși păcatul X = t, dar și tg X = t si ctg X = t .

Exemplul 8. Găsi integrală a unei funcții trigonometrice

.

Soluţie. Să schimbăm variabila: , apoi . Integrandul rezultat poate fi integrat cu ușurință folosind tabelul de integrale:

.

Exemplul 9. Găsi integrală a unei funcții trigonometrice

Soluţie. Să transformăm tangenta în raportul dintre sinus și cosinus:

Să schimbăm variabila: , apoi . Integrandul rezultat este tabel integral cu semnul minus:

.

Revenind la variabila inițială, obținem în sfârșit:

.

Exemplul 10. Găsi integrală a unei funcții trigonometrice

Soluţie. Să schimbăm variabila: , apoi .

Să transformăm integrantul pentru a aplica identitatea trigonometrică :

Schimbăm variabila, fără a uita să punem semnul minus în fața integralei (vezi mai sus, ce este egal cu dt). În continuare, factorizăm integrandul și integrăm folosind tabelul:

Revenind la variabila inițială, obținem în sfârșit:

.

Găsiți singur integrala unei funcții trigonometrice și apoi uitați-vă la soluție

Substituție trigonometrică universală

Substituție trigonometrică universală poate fi utilizat în cazurile în care integrantul nu se încadrează în cazurile discutate în paragrafele precedente. Practic, atunci când sinusul sau cosinusul (sau ambele) se află în numitorul unei fracții. S-a dovedit că sinusul și cosinusul pot fi înlocuite cu o altă expresie care conține tangenta jumătății unghiului inițial, după cum urmează:

Dar rețineți că substituția trigonometrică universală implică adesea transformări algebrice destul de complexe, deci este cel mai bine utilizată atunci când nicio altă metodă nu funcționează. Să ne uităm la exemple în care, împreună cu substituția trigonometrică universală, se utilizează substituția sub semn diferențial și metoda coeficienților nedeterminați.

Exemplul 12. Găsi integrală a unei funcții trigonometrice

.

Soluţie. Soluţie. Să profităm substituție trigonometrică universală. Apoi
.

Înmulțim fracțiile din numărător și numitor cu , și le scoatem pe cele două și le punem în fața semnului integral. Apoi