Диофанттың өмірбаяны. Диофанттың өмірбаяны Диофанттың қысқаша өмірбаяны

Кіріспе

Бір жарым мың жылдан астам уақыт ішінде Грекиядағы математика ғылымының айтарлықтай жетістіктерге жеткенін көруге болады.

Математика тарихында біз қарастырған Александрия мектебінің өмір сүрген кезеңі «Бірінші Александрия мектебі» деп аталады. Біздің дәуіріміздің басынан Александриялық математиктердің еңбектеріне сүйене отырып, идеалистік философияның қарқынды дамуы басталды: Платон мен Пифагордың идеялары қайтадан жанданды және неоплатонистер мен неопифагоршылардың бұл философиясы тез арада ғылыми маңыздылығын төмендетті. математикалық ойдың жаңа өкілдерінің еңбектері. Бірақ математикалық ой өшпейді, бірақ кейде Диофант сияқты жекелеген математиктердің еңбектерінде пайда болады.

Алгебраның дамуына таңбалық белгілердің әлі жеткілікті түрде қолданыла қоймауы кедергі болды, оның тұспалдарын біз Диофанттың еңбектерінде бірінші рет кездестіреміз, ол тек жеке белгілер мен белгілердің қысқартуларын қолданды.

Жұмыстың мақсаты - Диофанттың арифметикасын зерттеу.

Диофанттың өмірбаяны

Диофант ғылым тарихындағы ең қиын жұмбақтардың бірін ұсынады. Біз оның қай уақытта өмір сүргенін де, сол салада қызмет еткен бұрынғыларын да білмейміз. Оның шығармалары өтпес қараңғылықтың ортасындағы жарқыраған от іспетті.

Диофант өмір сүре алатын уақыт кезеңі жарты мыңжылдық! Бұл интервалдың төменгі шегі еш қиындықсыз анықталады: Диофант өзінің көпбұрышты сандар туралы кітабында б.з.б. Екінші жағынан, Александриялық Теонның атақты астроном Птолемейдің «Алмагестіне» берген түсініктемелерінде Диофанттың жұмысынан үзінді берілген. Теон біздің дәуіріміздің 4-ші ғасырдың ортасында өмір сүрген. Бұл осы интервалдың жоғарғы шегін анықтайды. Сонымен, 500 жыл!

Француз ғылым тарихшысы, Диофанттың ең толық мәтінін шығарушы Пол Таннери бұл олқылықты азайтуға тырысты. Escurial кітапханасынан ол 11 ғасырдағы Византия ғалымы Майкл Пселлостың хатынан үзінділерді тапты, онда «ең білімді Анатолий бұл ғылымның ең маңызды бөліктерін жинағаннан кейін (біз ғылыми дәрежелерді енгізу туралы айтып отырмыз) белгісіз және олардың белгілері), оларды досы Диофантқа арнады. Анатолий Александриялық шын мәнінде «Арифметикаға кіріспе» құрастырды, оның үзінділері Ямблих пен Евсевийдің сақталған еңбектерінде келтірілген. Бірақ Анатолий біздің дәуіріміздің 3-ші ғасырдың ортасында Александрияда өмір сүрді. және одан да дәлірек - 270 жылға дейін, ол Лаодакия епископы болғанға дейін. Демек, оның бәрі Александрия деп атайтын Диофантпен достығы осыдан бұрын болған болуы керек. Сонымен, атақты Александриялық математик пен Анатолийдің Диофант есімді досы бір адам болса, Диофанттың өмір сүрген уақыты біздің дәуіріміздің 3-ші ғасырдың ортасы.

Диофанттың «Арифметикасының» өзі «Кіріспе» мәтінінен көрініп тұрғандай, арифметика мен оны оқытуға қызығушылық танытқан «құрметті Дионисийге» арналған. Ол кезде Дионисий есімі өте кең таралған болса да, Таннери «қадірлі» Дионисийді көрнекті лауазымдарды атқарған дәуірдің атақты адамдарынан іздеу керек деп ұсынды. Сонымен, 247 жылы белгілі бір Дионисий Александрияның епископы болды, ол 231 жылдан бері қаладағы христиан гимназиясын басқарды! Сондықтан Таннери бұл Дионисийді Диофант өз жұмысын арнаған адаммен сәйкестендірді және Диофант біздің дәуіріміздің 3-ші ғасырдың ортасында өмір сүрген деген қорытындыға келді. Бізде жақсы нәрсе болмағандықтан, бұл күнді қабылдай аламыз.

Бірақ Диофанттың тұрғылықты жері белгілі - бұл әйгілі Александрия, эллиндік әлемнің ғылыми ойының орталығы.

Ескендір Зұлқарнайынның алып империясы ыдырағаннан кейін, Египет б.з.б. өзінің қолбасшысы Птолемей Лагусқа барды, ол астананы жаңа қалаға - Александрияға көшірді. Көп ұзамай бұл көптілді сауда қаласы ежелгі дәуірдің ең әдемі қалаларының біріне айналды. Рим кейінірек көлемі жағынан одан асып түсті, бірақ ұзақ уақыт бойы оның теңдігі болмады. Дәл осы қала көптеген ғасырлар бойы ежелгі дүниенің ғылыми және мәдени орталығына айналды. Бұл Птолемей Лагустың Мұражайды, Музалар ғибадатханасын, ең көрнекті ғалымдар шақырылған және олардың негізгі қызметі рефлексия мен әңгімелесу болатындай мазмұнды тағайындайтын бірінші Ғылым академиясы сияқты нәрсені құруымен байланысты болды. студенттермен. Музейде әйгілі кітапхана салынды, оның ең жақсы күндерінде 700 000-нан астам қолжазбалар болды. Әлемнің түкпір-түкпірінен ғалымдар мен білімге құштар жастардың Александрияға ағылып, әйгілі философтарды тыңдау, астрономия мен математиканы үйрену және кітапхананың салқын залдарында бірегей қолжазбаларды зерттеуге мүмкіндік алуы ғажап емес. .

Мұражай Птолемей әулетінен аман қалды. Біздің эрамызға дейінгі алғашқы ғасырларда. ол Рим жаулап алуларына байланысты Птоломей үйінің жалпы құлдырауымен байланысты уақытша құлдырауға түсті (Александрия ақыры б.з.д. 31 ж. жаулап алынды), бірақ содан кейін біздің дәуіріміздің бірінші ғасырларында. ол Рим императорларының қолдауымен қайта жанданды. Александрия әлемнің ғылыми орталығы болып қала берді. Бұл жағынан Рим ешқашан оған қарсылас болған емес: римдік ғылым (біз жаратылыстану ғылымдарын айтамыз) жай ғана болған жоқ, ал римдіктер Вергилийдің өсиеттеріне адал болып қалды, ол былай деп жазды:

Басқалары өмір беретін қоланы жақсырақ соғады, -

Мен олар мәрмәрден тірі тұлға жасайды деп сенемін,

Соттарда аспанның қимылдары шешен болады

Таяқтарымен олар жұлдыздарды сызып, есептейді,

Сен, Роман, халықтарды билейсің.

Ал егер б.з.б. III-II ғасырларда. Мұражай Евклид, Аполлоний, Эратосфен, Гиппарх есімдерімен жарқырайды, содан кейін біздің эрамыздың 1-3 ғасырларында. Мұнда Герон, Птоломей, Диофант сынды ғалымдар еңбек етті.

Диофанттың жеке басы туралы бәрін сарқыту үшін біз бізге жеткен жұмбақ өлеңді ұсынамыз:

Диофанттың күлі қабірде жатыр; оған таң қалдырыңыз - және тас

Марқұмның жасы дана өнері арқылы сөйлейді.

Тәңірдің қалауымен ол балалық шағында өмірінің алтыдан бір бөлігін өткізді.

Ал мен бес жарымда бетімнен қылтиып кездестім.

Сүйген қызына құда түскеніне жетінші күн ғана еді.

Онымен бес жыл бірге болған данышпан баласын күтті;

Әкесінің сүйікті ұлы өмірінің жартысын ғана өткізді.

Оны әкесінен ерте бейітінің жанынан алып кеткен.

Екі жыл бойы ата-ана ауыр қайғыны жоқтады,

Міне, мен мұңды өмірімнің шегін көрдім.

Осы жерден Диофанттың 84 жыл өмір сүргенін есептеу оңай. Дегенмен, бұл үшін сізге Диофанттың өнерін меңгерудің қажеті жоқ! Бір белгісізмен 1-дәрежелі теңдеуді шеше білу жеткілікті, ал мысырлық хатшылар мұны б.з.б. 2 мың жыл бұрын жасай алған.

Қалалық білім беру мекемесі

«No10 лицей» Пермь қ

Диофант. Диофантиндік теңдеулер

Тапсырма орындалды

Ильина Яна,

11 сынып оқушысы

Жетекші

Золотухина Л.В.

математика мұғалімі

Пермь, 2010 ж

Кіріспе……………………………………………………………………………….3

1. Диофант………………………………………………………………………………4.

2. Сандар мен таңбалар………………………………………………6

3. Диофантин теңдеуі…………………………………………8.

4. Шешімдер……………………………………………………..12

Қорытынды…………………………………………………………………………………15

Әдебиеттер……………………………………………………16

Кіріспе

Қазіргі мектеп оқушылары әртүрлі теңдеулерді шешеді. Бірыңғай мемлекеттік емтихан тапсырмаларының С бөлімінде Диофантин теңдеуі деп аталатын қызықты теңдеу бар. Диофант өз еңбектерінде рационал сандардағы анықталмаған теңдеулерді шешу мәселесін қойып қана қоймай, оларды шешудің кейбір жалпы әдістерін де берді. Математикадан емтихан тапсырғалы отырған бүгінгі он бірінші сынып оқушылары үшін бұл әдістердің пайдасы зор.

Диофант математиканың дамуына Архимед сияқты үлкен үлес қосты. Архимед осылай істеді, мысалы: эллипстің аудандарын, параболаның кесіндісін, шардың бетін, шардың және басқа денелердің көлемдерін анықтағанда интегралдық қосындылар әдісін және өту әдісін қолданды. шегіне дейін, бірақ ол еш жерде бұл әдістерге жалпы дерексіз сипаттама бермеген. 16-17 ғасырлардағы ғалымдарға Архимедтің әдістерін сол жерден оқшаулау үшін оның еңбектерін мұқият зерттеп, жаңаша ретке келтіруге тура келді. Диофантпен де жағдай ұқсас. Оның әдістерін Вьете мен Ферма түсінді және жаңа мәселелерге қолданды, яғни. сол уақытта Архимед шешілді.

1. Диофант

Диофант ғылым тарихындағы ең қиын жұмбақтардың бірін ұсынады. Біз оның қай уақытта өмір сүргенін де, сол салада қызмет еткен бұрынғыларын да білмейміз. Оның шығармалары өтпес қараңғылықтың ортасындағы жарқыраған от іспетті. Диофант өмір сүре алатын уақыт кезеңі жарты мыңжылдық! Бұл интервалдың төменгі шегі еш қиындықсыз анықталады: Диофант өзінің көпбұрышты сандар туралы кітабында б.з.б. e. Екінші жағынан, Александриялық Теонның атақты астроном Птолемейдің «Алмагестіне» берген түсініктемелерінде Диофанттың жұмысынан үзінді берілген. Теон біздің дәуіріміздің 4-ші ғасырдың ортасында өмір сүрген. e. Бұл осы интервалдың жоғарғы шегін анықтайды. Сонымен, 500 жыл!

Бірақ Диофанттың тұрғылықты жері белгілі - бұл әйгілі Александрия, эллиндік әлемнің ғылыми ойының орталығы.

Диофанттың жеке басы туралы бәрін сарқыту үшін біз бізге жеткен жұмбақ өлеңді ұсынамыз:

Диофанттың күлі қабірде жатыр; оған таң қалдырыңыз - және тас
Марқұмның жасы дана өнері арқылы сөйлейді.
Тәңірдің қалауымен ол балалық шағында өмірінің алтыдан бір бөлігін өткізді.
Ал мен бес жарымда бетімнен қылтиып кездестім.
Сүйген қызына құда түскеніне жетінші күн ғана еді.
Онымен бес жыл бірге болған данышпан баласын күтті;
Әкесінің сүйікті ұлы өмірінің жартысын ғана өткізді.
Оны әкесінен ерте бейітінің жанынан алып кеткен.
Екі жыл бойы ата-ана ауыр қайғыны жоқтады,
Міне, мен мұңды өмірімнің шегін көрдім.

Осы жерден Диофанттың 84 жыл өмір сүргенін есептеу оңай. Дегенмен, бұл үшін сізге Диофанттың өнерін меңгерудің қажеті жоқ! Бір белгісізмен 1-дәрежелі теңдеуді шеше білу жеткілікті, ал мысырлық хатшылар мұны б.з.б. 2 мың жыл бұрын жасай алған. e.

Бірақ ең жұмбақ - Диофанттың жұмысы. «Арифметикаға» біріктірілген 13 кітаптың алтауы бізге жетті. Бұл кітаптардың стилі мен мазмұны сандар теориясы мен алгебра бойынша классикалық ежелгі еңбектерден күрт ерекшеленеді, олардың мысалдарын біз Евклидтің элементтерінен, оның деректерінен және Архимед пен Аполлоний шығармаларынан леммалардан білеміз. «Арифметика» бізге мүлдем белгісіз болып қалған көптеген зерттеулердің нәтижесі екені сөзсіз. Біз оның тамыры туралы болжай аламыз және оның әдістері мен нәтижелерінің байлығы мен сұлулығына таңданамыз.

Диофанттың «Арифметикасы» есептердің жинағы (барлығы 189), олардың әрқайсысы шешіммен (немесе бірнеше шешу әдістерімен) және қажетті түсіндірмелермен жабдықталған. Сондықтан, бір қарағанда теориялық жұмыс емес сияқты. Дегенмен, мұқият оқу проблемалардың мұқият таңдалғанын және өте нақты, қатаң ойластырылған әдістерді көрсетуге қызмет ететінін көрсетеді. Ежелгі дәуірде әдеттегідей, әдістер жалпы түрде тұжырымдалмайды, бірақ ұқсас мәселелерді шешу үшін қайталанады.

2. Сандар мен белгілер

Диофант негізгі анықтамалардан және ол қолданатын әріп таңбаларының сипаттамасынан бастайды.

Классикалық грек математикасында Евклид элементтерінде άριJμός санымен аяқталды - « аритмос«немесе» арифмос"; сондықтан сандар туралы ғылым үшін «арифметика» атауы) бірліктердің жиынтығы ретінде түсінілді, яғни. бүтін сан. Бөлшектерді де, иррационалды да сандар деп атаған жоқ. Қатаң айтқанда, Принсипияда бөлшек жоқ. Бірлік бөлінбейтін болып саналады және бірлік бөлшектерінің орнына бүтін сандардың қатынасы қарастырылады; иррационалдықтар салыстыруға келмейтін кесінділердің қатынасы ретінде пайда болады, мысалы, біз қазір √2 деп белгілейтін сан классикалық гректер үшін квадраттың диагоналінің оның қабырғасына қатынасы болды. Теріс сандар туралы әңгіме болған жоқ. Тіпті олардың баламасы да болмады. Біз Диофанттан мүлде басқа суретті табамыз.

Диофант санның дәстүрлі анықтамасын бірліктердің жиынтығы ретінде береді, бірақ кейінірек оның мәселелерін іздейді оң рационалдышешімдерді және әрбір осындай шешімді сан деп атайды (άριJμός - “ аритмос »).

Бірақ іс мұнымен бітпейді. Диофант теріс сандарды енгізеді: ол оларды λει̃ψις арнайы термині деп атайды - « лейпсис" - λει̃πω етістігінен алынған - " лейпо», бұл жетіспеушілік, жетіспеушілік дегенді білдіреді, сондықтан терминнің өзін «жетпеушілік» деген сөзбен аударуға болады. Айтпақшы, орыстың атақты ғылым тарихшысы И.Тимченко осылай істейді. Диофант оң санды ΰπαρξις сөзі деп атайды - « iparxis”, бұл бар болу, болу дегенді білдіреді және көпше түрде бұл сөз мүлікті немесе мүлікті білдіруі мүмкін. Осылайша, Диофанттың салыстырмалы сандарға арналған терминологиясы Шығыс пен Еуропадағы орта ғасырларда қолданылған терминдерге жақын. Бұл жай ғана грек тілінен араб, санскрит, латын, содан кейін Еуропаның әртүрлі тілдеріне аудармасы болса керек.

λει̃ψις термині « лейпсис" - Диофанттың көптеген аудармашылары сияқты "алып тасталды" деп аудару мүмкін емес, өйткені азайту операциясы үшін Диофант мүлдем басқа терминдерді пайдаланады, атап айтқанда άφελει̃ν - " афелеин"немесе άφαιρει̃ν -" afirerain", олар άφαιρεω етістігінен жасалған - " афирео«- ала кету. Теңдеулерді түрлендіру кезінде Диофанттың өзі «екі жағына λει̃ψις қосу» стандартты өрнекті жиі қолданады.

Диофанттың терминдерін «жағымды» және «теріс» деп аударсақ, шындықтан таймайтынымызға оқырманның көзін жеткізу үшін Диофант мәтінінің филологиялық талдауына осылайша егжей-тегжейлі тоқталдық.

Диофант салыстырмалы сандар үшін белгілер ережесін тұжырымдайды:

«Теріске көбейтілген теріс оңды береді, ал оңға көбейтілген теріс теріс мәнді береді, ал теріс үшін айырушы белгі - инверттелген және қысқартылған (әріп) ψ».

«Мен сізге көбейтуді түсіндіргеннен кейін ұсынылған терминдердің бөлінуі де түсінікті болды; Енді осындай терминдерді қосу, азайту және көбейтуге жаттыға бастаған дұрыс. Оң немесе бірдей оң және теріс болып табылатын басқа мүшелерге коэффициенттері әртүрлі оң және теріс мүшелерді қосыңыз, ал оң және басқа теріс мүшелерден басқа оң және бірдей оң және теріс мүшелерді азайтыңыз».

Диофант тек рационалды оң шешімдерді іздегенімен, аралық есептеулерде теріс сандарды ықыласпен қолданатынын ескеріңіз.

Осылайша, Диофанттың сан өрісін арифметиканың барлық төрт амалын еш кедергісіз орындауға болатын рационал сандар өрісіне дейін кеңейткенін атап өтуге болады.

3. Диофантин теңдеуі

Анықтама – алгебралық теңдеулер немесе бүтін коэффициенттері бар, белгісіздер саны теңдеулер санынан асатын және бүтін немесе рационал шешімдер ізделетін алгебралық теңдеулер жүйесі.

балта + бойынша = 1

Қайда АЖәне б- қос жай бүтін сандар

Қосалқы сандарбарлық осы сандардың ортақ бөлгіштері тек + 1 және - 1 болатындай бірнеше бүтін сандар. Жай сандар жұбының ең кіші еселігі олардың көбейтіндісіне тең.

шексіз көп шешімдері бар:

Егер x0Және y0- бір шешім, содан кейін сандар

X = x0 + млрд

сағ = y0 -а

(n- кез келген бүтін сан) да шешімдер болады.

Тағы бір мысал Д. у.

x2 + y2 = z2

Бұл теңдеудің оң бүтін шешімдері катеттердің ұзындықтарын көрсетеді X , сағжәне гипотенуза zқабырғаларының ұзындығы бүтін тікбұрышты үшбұрыштар Пифагор сандары деп аталады.

Қабырғаларының ұзындығы осы сандарға пропорционал (немесе тең) үшбұрыш тікбұрышты болатындай натурал сандардың үштіктері.

Формулалардың көмегімен қарапайым Пифагор сандарының барлық үштіктерін алуға болады

X = м2 - n2

сағ = 2mn

z = м2 + n2

Қайда мЖәне n- бүтін сандар ( м > n > 0).

Бұл теңдеу жазықтықта анықталады Р 2 алгебралық қисықΓ. Біз ұтымды шешім деп атаймыз (2) рационалды нүктеқисығы Γ. Бұдан әрі біз геометрия тіліне жиі жүгінетін боламыз, дегенмен Диофанттың өзі оны еш жерде қолданбайды. Дегенмен, геометриялық тіл қазір математикалық ойлаудың ажырамас бөлігіне айналғаны сонша, оның көмегімен көптеген фактілерді түсіну және түсіндіру оңайырақ болады.

Ең алдымен, (2) теңдеулердің немесе алгебралық қисықтардың бірдей классификациясын беру қажет. Ең табиғи және ең ерте пайда болатыны олардың реті бойынша жіктелуі болып табылады.

Естеріңізге сала кетейік қалпында(2) қисығы – көпмүше мүшелерінің максимум реті f (x , ж), мұнда терминнің реті өкілеттіктердің қосындысы ретінде түсініледі xЖәне ж. Бұл ұғымның геометриялық мағынасы түзу сызықтың реттілік қисығын қиып өтуі nдәл сағатта nұпай. Нүктелерді санау кезінде, әрине, қиылысу нүктелерінің көптігін, сондай-ақ күрделі және «шексіз алыс» нүктелерді ескеру қажет. Мәселен, мысалы, шеңбер x 2 + ж 2 = 1 және түзу x + ж= 2 екі күрделі нүктеде және гиперболада қиылысады x 2 – ж 2 = 1 және түзу ж =x- шексіздіктегі екі нүктеде түзу сызықпен бірдей гипербола x=1 санының 2-көбейтіндісінің бір ортақ нүктесі бар.

Дегенмен, мақсаттар үшін диофантиндік талдау(бұл атау анықталмаған теңдеулерді шешу есептерінен пайда болған математика саласына берілді; бірақ қазір оны жиі диофант геометриясы деп атайды) реті бойынша жіктеу тым өрескел болып шықты.

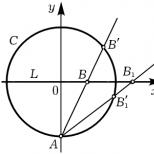
Күріш. 1.

Мұны мысалмен түсіндірейік. Шеңбер берілсін C : x 2 + ж 2 = 1 және рационал коэффициенттері бар кез келген түзу, мысалы, Л : ж=0. Осы шеңбер мен түзудің рационал нүктелерін бір-бірден сәйкестікке қоюға болатынын көрсетейік. Мұны, мысалы, келесідей жасауға болады: нүктені түзетіңіз А(0,–1) шеңберлер және әрбір рационал нүктені тағайындаңыз БТүзу Лнүкте B»шеңбер C, қиылысында жатыр Cжәне түзу AB(Cурет 1). Бұл нүктенің координаталары B»ұтымды болады, біз оны оқырманға өзі дәлелдеуге мүмкіндік береміз немесе Диофанттың ұқсас дәлелін оқимыз (ол келесі абзацта ұсынылады). Кез келген конус қимасының рационал нүктелері арасында, егер оның үстінде кем дегенде бір рационал нүкте жатса және рационал сызық арасында бірдей сәйкестік орнатуға болатыны анық. Диофантиндік талдау тұрғысынан шеңберді көреміз Cжәне түзу Лажыратылмайды: олардың рационал шешімдер жиыны эквивалентті. Және бұл екі қисықтың реттері әртүрлі болғанына қарамастан.

Алгебралық қисықтарды тек 19 ғасырда ғана Абель мен Риман енгізген. Бұл жіктеу Γ қисығының ерекше нүктелерінің санын ескереді.

Γ қисығының (2) теңдеуінде көпмүше деп есептейміз f (x , ж) рационал сандар өрісінде азайтылмайтын, яғни. ол рационал коэффициенттері бар көпмүшелердің көбейтіндісіне кеңеймейді. Белгілі болғандай, нүктедегі Γ қисығына жанаманың теңдеуі П (x 0 , ж 0) болады

ж – ж 0 = к (x – x 0),

Егер нүктеде Птуынды fx"немесе ж»нөлден ерекшеленеді, содан кейін еңіс кжанаманың өте нақты мағынасы бар (егер ж» (x 0 , ж 0) = 0, a fx" (x 0 , ж 0) ≠ 0, содан кейін к=∞ және жанама Птік болады).

Егер нүктеде Пекі жартылай туынды да жойылады,

fx" (x 0 , ж 0) = 0 және ж» (x 0 , ж 0) = 0,

содан кейін көрсетіңіз Пшақырды арнайы .

Мысалы, қисық сызықта ж 2 = x 2 + x 3 ұпай (0, 0) ерекше болады, өйткені онда fx" = –2x – 3x 2 және ж» = 2жнөлге барыңыз.

Күріш. 2.

Ең қарапайым сингулярлық нүктелер қос нүктелер болып табылады, оларда туындылардың кем дегенде біреуі болады f xx "" , f xy ""Және f жж ""нөлден ерекшеленеді. Суретте. 2-суретте қисық екі түрлі жанама болатын қос нүкте көрсетілген. Басқа күрделірек ерекше нүктелер суретте көрсетілген. 3.

Күріш. 3.

4. Шешімдер

Ереже 1. Егер с d-ге бөлінбесе, онда ax + vy = c теңдеуінің бүтін сандардағы шешімі жоқ. N.O.D.(a,b) = d.

2-ереже. a және b қосындысы бар ax+vy = c теңдеуінің шешімін табу үшін алдымен ax+y = 1 теңдеуінің шешімін (X o; y o) табу керек; CX o, Su o сандары ax + vy = c теңдеуінің шешімін құрайды.

Бүтін сандардағы теңдеуді шешу (x,y)

5x - 8y = 19 ... (1)

Бірінші жол. Таңдау әдісі арқылы белгілі бір шешімді табу және жалпы шешімді жазу.

Біз білеміз, егер N.O.D.(a;b) =1, яғни. a және b қос жай сандар, содан кейін (1) теңдеу

х және у бүтін сандарында шешімі бар. N.O.D.(5;8) =1. Таңдау әдісі арқылы белгілі бір шешімді табамыз: X o = 7; y o =2.

Сонымен, (7;2) сандар жұбы (1) теңдеудің нақты шешімі болып табылады.

Бұл теңдік орындалатынын білдіреді: 5 x 7 – 8 x 2 = 19 ... (2)

Сұрақ: Бір шешім берілгенде, қалған барлық шешімдерді қалай жазу керек?

(1) теңдеуінен (2) теңдігін алып тастап, мынаны алайық: 5(х -7) – 8(у - 2) =0.

Демек, x – 7 =. Алынған теңдіктен (x – 7) санының бүтін болатыны, егер (y – 2) 5-ке бөлінетін болса ғана анық болады, яғни. y – 2 = 5n, мұндағы n – кейбір бүтін сан. Сонымен, y = 2 + 5n, x = 7 + 8n, мұндағы n Z.

Осылайша, бастапқы теңдеудің барлық бүтін шешімдерін келесі түрде жазуға болады:

Екінші жол . Бір белгісізге теңдеуді шешу.

Бұл теңдеуді ең кіші (модульдік) коэффициенті бар белгісізге қатысты шешеміз. 5x - 8y = 19 x =.

5-ке бөлгендегі қалдық: 0,1,2,3,4. Осы сандарды у орнына қойып көрейік.

Егер у = 0 болса, онда x = =.

Егер у = 1 болса, онда x = =.

Егер у = 2 болса, онда x = = = 7 Z.

Егер у = 3 болса, онда x = =.

Егер у = 4 болса, онда x = =.) Қорытынды

Сонымен қатар, ғылым тарихшыларының көпшілігі, математиктерге қарағанда, Диофанттың еңбектерін осы уақытқа дейін жете бағаламады. Олардың көпшілігі Диофанттың бір ғана шешім табумен шектелгеніне сенді және бұл үшін әртүрлі мәселелер үшін әртүрлі жасанды әдістерді қолданды. Бірақ шын мәнінде, диофант теңдеулерінің көпшілігінде біз ұқсас шешім алгоритмдерін байқаймыз.

Бүгінгі күні, біз көріп отырғанымыздай, алгоритмдерін есте сақтау оңай болатын бірнеше түрлі шешімдер бар. Бұрын айтылғандай, бұл теңдеу әдетте Бірыңғай мемлекеттік емтихандағы C6 тапсырмасында кездеседі. Диофантиндік теңдеулерді шешу алгоритмдерін зерттеу бұл тапсырманы шешуге көмектеседі, бұл маңызды ұпай санына тұрарлық.

Әдебиеттер тізімі

1. Александриялық Диофант. Арифметика және көпбұрышты сандар туралы кітап (Ежелгі грек тілінен аудармасы И. Н. Веселовский; редакциялау және түсініктемелер И. Г. Башмакова). М., «Ғылым», 1974 ж.

2. B. L. Van der Waerden, Ояну ғылымы (аудармасы И. Н. Веселовский). М., Физматғыз, 1959 ж.

3. Г.Г.Цейтен, Антикалық және орта ғасырлардағы математика тарихы (П. Юшкевичтің аудармасы). М.–Л., Гостехиздат, 1932 ж

4. А.В.Васильев, бүтін сан. Петербург, 1919 ж

5. И.В.Ященко, С.А.Шестаков, П.И.Захаров, математика, Бірыңғай мемлекеттік емтихан, МТСНМО, 2010 ж.

Сегізаяқта 8 аяқ, теңіз жұлдызында 5 аяқ бар.

Барлығы 39 мүше болса, аквариумда қанша теңіз жануары бар?

Александриялық Диофант - ежелгі грек математигі, ол біздің дәуіріміздің 3 ғасырында өмір сүрген.

Оның өмірінің егжей-тегжейлері туралы ештеңе дерлік белгісіз. Бір жағынан, Диофант Hypsicles (б.з.б. 2 ғ.) келтіреді; екінші жағынан, Теон Александриялық (шамамен 350 ж.) Диофант туралы жазады, одан оның өмірі осы кезеңнің шегінде өтті деген қорытынды жасауға болады. Диофанттың өмір сүрген уақытын нақтылау оның «Арифметикасының» «ең құрметті Дионисийге» арналғандығына негізделген. Бұл Дионисий 3 ғасырдың ортасында өмір сүрген Александрия епископы Дионисийден басқа ешкім емес деп саналады. n. e.

Палатина антологиясында эпиграмма-тапсырма бар, одан Диофант 84 жыл өмір сүрді деген қорытынды жасауға болады:

Диофанттың күлі қабірде жатыр; оған және тасқа таң қалды

Марқұмның жасы дана өнері арқылы сөйлейді.

Тәңірдің қалауымен ол балалық шағында өмірінің алтыдан бір бөлігін өткізді.

Ал мен бес жарымда бетімнен қылтиып кездестім.

Жетінші күн өткенде ол сүйіктісіне құда түсіпті.

Онымен бес жыл бірге болған данышпанның ұлы болды;

Әкесінің сүйікті ұлы өмірінің жартысын ғана өткізді.

Оны әкесінен ерте бейітінің жанынан алып кеткен.

Екі жыл бойы ата-ана ауыр қайғыны жоқтады,

Міне, мен мұңды өмірімнің шегін көрдім.

Теңдеулерді шешудің заманауи әдістерін қолдана отырып, Диофанттың қанша жыл өмір сүргенін есептеуге болады. Теңдеуді құрайық және шешейік:

Бұл теңдеудің шешімі 84 саны. Осылайша Диофант 84 жыл өмір сүрді.

Диофанттың негізгі жұмысы 13 кітаптан тұратын «Арифметика». Өкінішке орай, 13 кітаптың алғашқы 6-сы ғана сақталған.

Бірінші кітаптың алдында Диофант пайдаланған белгілерді сипаттайтын кең көлемдегі кіріспе бар. Диофант белгісізді «сан» (?ριθμ?ς) деп атайды және оны ς әрпімен, белгісіздің квадратын таңбамен (δ?ναμις – «дәреже») қысқаша белгілейді. Куб-куб деп аталатын алтыншыға дейінгі белгісіздің келесі дәрежелері үшін және оларға қарама-қарсы дәрежелер үшін арнайы белгілер қарастырылған. Диофанттың қосу белгісі жоқ: ол жай ғана оң мүшелерді бір-бірінің қасына жазады, ал әрбір мүшеде алдымен белгісіздің дәрежесі, содан кейін сандық коэффициент жазылады. Шегерілген мүшелер де қатар жазылады және олардың бүкіл тобының алдына инверттелген Ψ әрпі түріндегі арнайы белгі қойылады. Теңдік белгісі екі әріппен белгіленеді ?σ (?σος қысқартылған – «тең»). Ұқсас мүшелерді келтіру ережесі және теңдеудің екі жағына бірдей санды немесе өрнекті қосу немесе азайту ережесі тұжырымдалған: әл-Хорезми кейін оны «әл-жабр және әл-муқабала» деп атады. Белгі ережесі енгізілді: минус есе минус плюс береді; Бұл ереже шегерілген мүшелері бар екі өрнекті көбейту кезінде қолданылады. Мұның бәрі геометриялық интерпретацияларға сілтеме жасамай, жалпы түрде тұжырымдалған.

Жұмыстың көпшілігі шешімдері бар есептер жинағы (алты кітапта барлығы 189 бар), жалпы әдістерді суреттеу үшін шебер таңдалған. «Арифметиканың» негізгі мәселесі – анықталмаған теңдеулердің оң рационал шешімдерін табу. Рационал сандарды Диофант натурал сандармен бірдей түсіндіреді, бұл ежелгі математиктерге тән емес.

Біріншіден, Диофант 2 белгісіздегі 2 ретті теңдеулер жүйесін зерттейді; ол бұрыннан белгілі болса, басқа шешімдерді табу әдісін көрсетеді. Содан кейін ол жоғары дәрежелі теңдеулерге ұқсас әдістерді қолданады.

10 ғасырда «Арифметика» араб тіліне аударылды, содан кейін ислам елдерінің математиктері (Әбу Камил және т.б.) Диофанттың кейбір зерттеулерін жалғастырды. Еуропада арифметикаға қызығушылық Рафаэль Бомбелли Ватикан кітапханасында осы жұмысты тауып, оның «Алгебрасында» (1572) 143 есепті жариялағаннан кейін артты. 1621 жылы Баче де Мезириак жасаған «Арифметиканың» классикалық, мұқият түсіндірмеленген латын тіліндегі аудармасы пайда болды. Диофанттың әдістері Франсуа Вьет пен Пьер Фермаға үлкен әсер етті; Гаусс пен Эйлер зерттеулерінің бастапқы нүктесі болды. Алайда қазіргі заманда анықталмаған теңдеулер әдетте Диофант сияқты рационалды емес, бүтін сандармен шешіледі.

20 ғасырда Диофант деген атпен арифметиканың тағы 4 кітабының арабша мәтіні ашылды. Кейбір математика тарихшылары осы мәтінді талдай келе, олардың авторы Диофант емес, Диофанттың әдістерін жақсы білетін комментатор, ең алдымен Гипатия деген гипотезаны алға тартты.

Диофанттың «Көпбұрышты сандар туралы» (Περ? πολυγ?νων ?ριθμ?ν) трактаты толық сақталған жоқ; сақталған бөлігінде геометриялық алгебра әдістерін қолдану арқылы бірқатар көмекші теоремалар шығарылады.

Диофанттың «Беттерді өлшеу туралы» (?πιπεδομετρικ?) және «Көбейту туралы» (Περ? πολλαπλασιασμο?) шығармаларынан да фрагменттері ғана сақталған.

Диофанттың «Поризмдер» кітабы арифметикада қолданылатын бірнеше теоремалар арқылы ғана белгілі.

Бүгінгі күні теңдеу пішінде

Қайда П- бүтін функция (мысалы, бүтін коэффициенттері бар көпмүше), ал айнымалылар ежелгі грек математигі - Диофантиннің құрметіне аталатын бүтін мәндерді қабылдайды.

Ең танымал диофант теңдеуі

Оның шешімдері Пифагор үштіктері: (3; 4; 5), (6; 8; 10), (5; 12; 13), (12; 35; 37)...

Диофант теңдеуінің бүтін сандардағы шешілмейтіндігін дәлелдеу

сағ (Ферманың соңғы теоремасы) ағылшын математигі Эндрю Уайлс 1994 жылы аяқтады.

Диофант теңдеуінің тағы бір мысалы - Пелл теңдеуі

параметр қайда nнақты шаршы емес.

Гильберттің оныншы есебі – Дэвид Гильберт 1900 жылы 8 тамызда екінші халықаралық математиктер конгресінде ұсынған 23 есептің бірі. Гильберттің баяндамасында оныншы есептің тұжырымы ең қысқасы:

Ерікті белгісіздер және бүтін рационал сандық коэффициенттері бар диофант теңдеуі берілсін. Бұл теңдеудің рационал бүтін сандарда шешілетіндігін анықтау үшін соңғы санды операциялардан кейін мүмкін болатын әдісті көрсетіңіз.

Бұл есептің алгоритмдік шешілмейтіндігін дәлелдеу шамамен жиырма жылға созылды және оны 1970 жылы Юрий Матиясевич аяқтады.

Көбінесе Александриялық Паппаның (III ғ.) қызметінің арқасында ежелгі ғалымдар мен олардың еңбектері туралы мәліметтер бізге жетті. Аполлонийден кейін (б.з.б. 2 ғасырдан) антикалық ғылымда құлдырау басталды. Жаңа терең идеялар пайда болмайды. 146 жж. e. Рим Грецияны басып алды, ал б.з.б. 31 ж. e. - Александрия. Жалпы тоқырау мен құлдырау аясында ежелгі ұлы математиктердің соңғысы, «алгебраның атасы» Александриялық Диофанттың алып тұлғасы күрт көзге түседі.

Келесі математикалық объектілер Диофанттың атымен аталған:

• диофантиндік талдау
• Диофантиндік жуықтаулар
• Диофантиндік теңдеулер

Алгебралық еңбектердің алғашқы авторларының бірі болып саналатын Александриядан шыққан ежелгі грек математигі. Орта ғасырларда оны «алгебраның атасы» деп атаған.

Ол бізге жетті 6 бастап кітаптар 13 4-дәрежеге дейінгі бірқатар алгебралық теңдеулердің шешімін беретін «Арифметика/Арифметика» трактатынан.

«Диофант алгебралық символизмнің жетекші идеясына ие - сандар орнына белгілерді пайдалану; бірақ ол оны толық пайдалана алмады. Ол «4 = 4х + 20 абсурдтық теңдеуді шешу мүмкін емес. Мүмкін емес пе? Абсурд теңдеу? Теңдеу теріс мәнге әкеледі: x = - 4. Диофант білмеген нөл ұғымынсыз теріс сан ұғымы логикалық тұрғыдан мүмкін емес. Диофанттың тамаша жаңалықтарын кейінгі ұрпақтар елемеген сияқты. Оның еңбегі еленіп, дұрыс бағаланғанға дейін он бес жүз жыл өтті: оның трактаты 17 ғасырда алгебраның гүлденуінде басты рөл атқарды. Бүгінгі күні барлығына белгілі a+bx=c түріндегі сызықтық алгебралық теңдеулер оның есімімен аталады».

Питер Бернштейн, құдайларға қарсы: Тәуекелді қолға түсіру, М., Olympus Business, 2006, 10-бет. XLVII-L.

«Арифметика есептер қатары ретінде берілген. Алғы сөзде Диофантоқушыларына проблемалық кітап ретінде жазғанын хабарлайды. Ол белгісіз үшін арнайы таңбаны, сондай-ақ оның шаршысы мен кубы үшін бөлек белгілерді пайдаланды; Бұл динамианың (қуат, күш) және кибостың (текше) жиырылулары сияқты. Белгілеу өте жақсы құрылымдалмаған. Диофант қосуды таңбаларды бір-бірінің қасына қою ретінде ғана жазады (біз мұны қазір көбейту үшін жасаймыз), бірақ ол азайту үшін арнайы таңбаны пайдаланады. Теңдік белгісі де бар, бірақ оны кейінірек көшіруші енгізген болуы мүмкін. Арифметика негізінен теңдеулерді шешуге арналған. Бірінші сақталған кітапта сызықтық теңдеулер талқыланады; қалған бесеуі квадрат теңдеулердің әртүрлі түрлерін, көбінесе бірнеше белгісіздерге, сондай-ақ кейбір арнайы текше теңдеулерге қатысты. Тән ерекшелігі - жауаптар әрқашан бүтін немесе рационал сандар. Бүгінгі таңда егер оның шешімдері бүтін сандармен немесе рационал сандармен шектелсе, оны Диофантин теңдеуін атаймыз».

Ян Стюарт, Ақиқат және сұлулық: симметрияның дүниежүзілік тарихы, М., «Астрель»; «Корпус», 2010, б. 68.

Мүмкін, Диофант 84 жыл өмір сүрді, бұл оған берілген эпитафиялық тапсырмадан: «Диофант өмірінің алтыншы бөлігін сәби кезінде, он екінші бөлігін жасөспірім кезінде өткізді; содан кейін ол үйленіп, өмірінің жетінші бөлігін және тағы бес жыл баласыз некеде өмір сүрді, содан кейін ол әкесінің жарты жасына ғана жеткен ұлы болды; әкесі ұлынан төрт жасқа артық өмір сүрді».

Шамасы, Диофант вавилондықтар мен мысырлықтардың ежелгі еңбектеріне сүйенген.

Александриялық Диофант(ежелгі грек Διόφαντος ὁ Ἀλεξανδρεύς ; лат. Диофант) — біздің эрамызға дейінгі 3 ғасырда өмір сүрген ежелгі грек математигі. e. Көбінесе «алгебраның атасы» деп аталады. «Арифметика» – анықталмаған теңдеулердің оң рационал шешімдерін табуға арналған кітаптың авторы. Қазіргі кезде «диофантиндік теңдеулер» әдетте бүтін коэффициенттері бар теңдеулерді білдіреді, олардың шешімдері бүтін сандар арасында табылуы керек.

Өмірбаяны [ | ]

Латын аудармасы Арифметика (1621)

Оның өмірінің егжей-тегжейлері туралы ештеңе дерлік белгісіз. Бір жағынан, Диофант Hypsicles (б.з.б. 2 ғ.) келтіреді; екінші жағынан, Теон Александриялық (шамамен 350 ж.) Диофант туралы жазады, одан оның өмірі осы кезеңнің шегінде өтті деген қорытынды жасауға болады. Диофанттың өмір сүру уақытын ықтимал нақтылау оның негізінде жатыр Арифметика«Ең құрметті Дионисийге» арналған. Бұл Дионисий 3 ғасырдың ортасында өмір сүрген Александрия епископы Дионисийден басқа ешкім емес деп саналады. n. e.

Ол келесі теңдеуді шешуге тең:

Бұл теңдеу береді x = 84 (\displaystyle x=84), яғни Диофанттың жасы 84 жасқа тең. Алайда ақпараттың дұрыстығын растау мүмкін емес.

АрифметикаДиофанта[ | ]

Диофанттың негізгі жұмысы - Арифметика 13 кітапта. Өкінішке орай, алғашқы 13 кітаптың тек 6 (немесе 10, төменде қараңыз) ғана сақталған.

Бірінші кітаптың алдында Диофант пайдаланған белгілерді сипаттайтын кең көлемдегі кіріспе бар. Диофант белгісіз «сан» деп атайды ( ἀριθμός ) және әріппен белгіленеді ς , шаршы белгісіз – таңба Δ Υ (қысқа δύναμις - «дәреже»), белгісіз текше - таңба Κ Υ (қысқа κύβος - «текше»). Куб-куб деп аталатын алтыншыға дейінгі белгісіздің келесі дәрежелері үшін және олардың қарама-қарсы градустары үшін минус алтыншыға дейін арнайы белгілер қарастырылған.

Диофанттың қосу белгісі жоқ: ол жай ғана оң мүшелерді бір-бірінің қасына дәреженің кему ретімен жазады және әрбір мүшеге алдымен белгісіздің дәрежесі, содан кейін сандық коэффициент жазылады. Шегерілген мүшелер де қатар жазылады және олардың бүкіл тобының алдына инверттелген Ψ әрпі түріндегі арнайы белгі қойылады. Теңдік белгісі екі әріппен белгіленеді ἴσ (қысқа ἴσος - «тең»).

Ұқсас мүшелерді келтіру ережесі және теңдеудің екі жағына бірдей санды немесе өрнекті қосу немесе азайту ережесі тұжырымдалған: әл-Хорезми кейін оны «алгебра және әлмукабала» деп атай бастады. Белгілер ережесі енгізілді: «минус плюс минус береді», «минус минус плюс береді»; Бұл ереже шегерілген мүшелері бар екі өрнекті көбейту кезінде қолданылады. Мұның бәрі геометриялық интерпретацияларға сілтеме жасамай, жалпы түрде тұжырымдалған.

Жұмыстың басым бөлігі шешімдері бар есептер жинағы (алты кітапта барлығы 189, араб бөлігіндегі төртеуімен бірге - 290 бар), жалпы әдістерді суреттеуге шебер таңдалған. Негізгі мәселелер Арифметика- анықталмаған теңдеулердің оң рационал шешімдерін табу. Рационал сандарды Диофант натурал сандар сияқты қарастырады, бұл ежелгі математиктерге тән емес.

Біріншіден, Диофант екі белгісіздегі екінші ретті теңдеулер жүйесін зерттейді; ол бұрыннан белгілі болса, басқа шешімдерді табу әдісін көрсетеді. Содан кейін ол жоғары дәрежелі теңдеулерге ұқсас әдістерді қолданады. VI кітапта қабырғалары ұтымды тікбұрышты үшбұрыштарға қатысты есептер қарастырылады.

Әсер ету Арифметикаматематиканы дамытуға арналған[ | ]

10 ғасырда Арифметикаараб тіліне аударылды, содан кейін ислам елдерінің математиктері (Әбу Камил және т.б.) Диофанттың кейбір зерттеулерін жалғастырды. Еуропада қызығушылық АрифметикаРафаэль Бомбелли бұл еңбекті латын тіліне аударып, басып шығарғаннан кейін өсті және оның 143 мәселесін өз кітабында жариялады. Алгебра(1572). 1621 жылы латын тіліндегі классикалық аудармасы пайда болды Арифметика, Баче де Мезирьяк орындаған.

Диофанттың әдістері Франсуа Вьет пен Пьер Фермаға қатты әсер етті; бірақ қазіргі заманда анықталмаған теңдеулер әдетте Диофант сияқты рационал сандармен емес, бүтін сандармен шешіледі. Пьер Ферма Баше де Мезирьяк өңдеген Диофанттың «Арифметиканы» оқығанда, ол Диофант қарастырған теңдеулердің бірінің бүтін сандармен шешімі жоқ деген қорытындыға келді және оның шетінде «шынында да керемет дәлелді тапқанын» атап өтті. бұл теорема ... дегенмен, кітаптың шеттері оны қосу үшін тым тар». Бұл мәлімдеме қазір Ферманың соңғы теоремасы ретінде белгілі.

20 ғасырда Диофант деген атпен тағы төрт кітаптың арабша мәтіні табылды. Арифметика. И.Г.Башмакова мен Е.И.Славутин бұл мәтінді талдай отырып, оның авторы Диофант емес, Диофанттың әдістерін жақсы білетін комментатор, ең алдымен Гипатия деген гипотезаны алға тартты. Дегенмен, алғашқы үш және соңғы үш кітаптағы есептерді шешу әдістемесіндегі айтарлықтай олқылықты араб тіліндегі аударманың төрт кітабы жақсы толтырады. Бұл бізді бұрынғы зерттеулердің нәтижелерін қайта қарауға мәжбүр етеді. . [ ]

Диофанттың басқа да жұмыстары[ | ]

Диофанттың трактаты Көпбұрышты сандар туралы (Περὶ πολυγώνων ἀριθμῶν ) толық сақталмаған; сақталған бөлігінде геометриялық алгебра әдістерін қолдану арқылы бірқатар көмекші теоремалар шығарылады.

Диофанттың шығармаларынан Беттерді өлшеу туралы (ἐπιπεδομετρικά ) Және Көбейту туралы (Περὶ πολλαπλασιασμοῦ ) сонымен қатар үзінділері ғана сақталған.

Диофант кітабы Поризмдерқолданылатын бірнеше теоремалар арқылы ғана белгілі Арифметика.