Дұрыс емес интегралдардың жинақтылық белгілері. Дұрыс емес интегралдар Анықтамасы және негізгі қасиеттері

12.11 теорема (дұрыс емес интегралдарды салыстыруға арналған тест). f(x) және g(x) функциялары [a, ">) интервалында үзіліссіз болсын және ондағы 0 fix) ?(x) шартын қанағаттандырсын. Содан кейін интегралдың жинақтылығынан

интегралдың жинақтылығы бойынша жүреді

және керісінше, (12.64) интегралының дивергенциясы (12.63) интегралының дивергенциясын білдіреді.

Дәлелдеу.Белгілеуді енгізейік:

Функция P(K)төмендемейді; шын мәнінде, егер және мен 2, содан кейін

Дж түзету) dx>0, содан кейін

Мәндер тізбегін алыңыз (/? „) -> “>; содан кейін функция мәндерінің сәйкес тізбегі (F(Rn))монотонды және төмендемейді. (12.63) интегралы жинақталсын, содан кейін (67) тізбегі Рол)) шектеулі; бірақ содан кейін реттілік те шектеулі (Ф(/?n)) және демек, 7.13 теоремасының күші бойынша ол жинақталады. Сондықтан шектеу бар F(R)сағ Р-+ ">, яғни. интегралды (12.64) жинақталады.

Енді теореманың екінші бөлігін дәлелдейміз; (12.64) интегралы диверсификациялансын. Егер (12.63) интеграл жинақталады деп алсақ, онда жоғарыда дәлелденген (12.64) интегралы да жинақталуы керек, бұл шартқа қайшы келеді. Теорема дәлелденді. ?

Түсініктеме.Осыған ұқсас салыстыру критерийі екінші текті дұрыс емес интегралдар үшін де жарамды. f(x) және функциялары болса g (X)жарты аралықта үздіксіз [a> b)және сингулярлық нүктенің кейбір маңындағы барлық нүктелер үшін борындалды

шарттар 0 (x), онда Jg(x)dx интегралының жинақтылығынан мынандай нәтиже шығады

J/(x)dx интегралы, ал J/(x)dx интегралының дивергенциясынан - дивергенция

Jg(x)dx интегралының көпірі.

Дұрыс емес интегралдардың жинақтылығын зерттеуге мысалдарды қарастырайық.

27-мысал. Т. ^-.

X 3 (1 + e L)

Шешім.Осы интегралдағы интегралды функциямен салыстырайық

Dg. Бұл анық -g- -

X r* (1+0 x Дж

J-jdx град жинақталады; сондықтан салыстыру критерийінің күшімен жинақталады және 1 X

ny интеграл.

28-мысал. I-.

Шешім.Осы интегралдың интегралды 1/x функциясымен салыстыру,

1 интервалында (1 + в х)/x > 1/x екенін көреміз

алшақтайды, демек, берілген интеграл салыстыру критерийі бойынша да алшақтайды.

Қорытындылай келе, бірінші текті дұрыс емес интегралдың жинақтылығының Коши критерийін дәлелсіз келтіреміз.

12.10.4. Дұрыс емес интегралдардың абсолютті және шартты жинақтылығы

Анықтама 5. J/(x)dx дұрыс емес интеграл деп аталады мүлдем

жинақтау, егер J|/(x)|dx интегралы жинақталса.

Анықтама 6. J /(x) dx дұрыс емес интегралы деп аталады шартты түрде ұқсас

жану, егер ол жинақталса және J|/(x)|dx интегралы ауытқыса.

Интегралдың абсолютті жинақтылығы оның анықталған интегралдың 3-бағасы және Коши критерийі арқылы жинақталуын білдіретінін ескеріңіз.

12.13 теоремасы (Дирихле-Абель сынағы*). f(x) функциясы үзіліссіз және шектелген антитуынды болсын Ф(x) [a, ">) интервалында, g(x) функциясының осы интервалда үзіліссіз туындысы болса, өспейді және x -> ©o ретінде нөлге ұмтылады. Содан кейін дұрыс емес интеграл

жинақталады.

Дәлелдеу. J /(x)g(x)dx интегралына бөліктер бойынша интегралдауды қолданамыз

ерікті сегментте R R"[мен А, °°). Бізде бар:

Теорема 12.12. Дұрыс емес интегралдың (12.64) жинақтылығы үшін кез келген e > 0 үшін мұндай санды табуға болатыны қажет және жеткілікті. А> 0, бұл кез келген үшін R"және /?", үлкенірек А,келесі теңсіздік орындалады:

Теорема бойынша F(x)шектеулі, яғни. |F(x)| K. g(x) функциясы өспейді және х -» «> ретінде нөлге ұмтылады, демек. g(x)> 0 және g"(x)

Абель Нильс Хенрик (1802-1829) норвег математигі.

Өйткені, теорема гипотезасы бойынша, g(x) -» 0 ретінде x -> ©°, үшін ерікті сан e > 0 нөмірді таба аласыз A>осылайша R"> Lтеңсіздік орындалады g(R") Мұны (12.68) бағалауға ауыстырсақ, мынаны аламыз:

ол интегралдың жинақтылығының Коши критерийіне сәйкес келеді (12.66). Теорема дәлелденді. ?

Дұрыс емес интегралдардың жинақтылығы үшін Дирихлет-Абель тестін қолдану мысалдарын қарастырыңыз.

29-мысал. f^^dx, a > 0.

Шешім.Біз / (x) \u003d sin x қоямыз, g(x)= l/x"; теореманың барлық шарттарының орындалғанын тексеру оңай, яғни бұл интеграл жинақталады. a > 1 үшін бұл интеграл

ral абсолютті түрде жақындайды. Шынында да, |күнә x/xP 1/d L, интегралды J(l/x e)dx

жинақталады, яғни. салыстыру арқылы (12.11 теорема), бұл интеграл да абсолютті жинақталады.

Мысал 30. Jsin x 2 dx - Френель интегралы, о

Шешім.Бұл интегралды қосынды түрінде көрсетеміз:

sin x 2 (0, 1J) кесіндісінде үзіліссіз функция болғандықтан (12.69) бірінші интеграл бар.(12.69) оң жағындағы бұрыс интегралдың жинақтылығын анықтау үшін / (x) \ қоямыз. u003d x sin x 2, g(x) = 1/x. Сонда f(x) функциясы үшін антитуынды F(x) = -cosx 2 /!|1, ">" интервалында шектелген, #(x) оң болса, x -» °° ретінде нөлге ұмтылады және (1, ©o) бойынша үздіксіз туындысы бар. Демек, Дирихле – Абель критерийі бойынша (12.69) екінші интеграл жинақталады, яғни. Френель интегралы да жинақталады.

Бірінші текті дұрыс емес интегралдар.Шын мәнінде, бұл бірдей анықталған интеграл, бірақ интегралдардың шексіз жоғарғы немесе төменгі интегралдау шегі бар немесе екі интегралдау шегі де шексіз болатын жағдайларда.

Екінші текті дұрыс емес интегралдар.Шындығында, бұл бірдей анықталған интеграл, бірақ интеграл шектелмеген функциялардан алынған жағдайларда, интегралдың шексіздікке айнала отырып, ақырлы кесіндінің ақырлы нүктелерінде интегралдауы болмайды.

Салыстыру үшін.Анықталған интеграл түсінігін енгізу кезінде функция деп ұйғарылды f(x) кесіндісінде үздіксіз [ а, б], ал интегралдау интервалы шекті, яғни ол шексіздікпен емес, сандармен шектеледі. Кейбір міндеттер бұл шектеулерден бас тарту қажеттілігіне әкеледі. Дұрыс емес интегралдар осылай пайда болады.

Дұрыс емес интегралдың геометриялық мағынасыөте қарапайым болып шығады. Функцияның графигі болғанда ж = f(x) осінен жоғары орналасқан Өгіз, анықталған интеграл ауданды өрнектейді қисық сызықты трапеция, шектелген қисық ж = f(x) , абсцисса және ордината x = а , x = б. Өз кезегінде, дұрыс емес интеграл сызықтар арасында шектелмеген (шексіз) қисық сызықты трапецияның ауданын өрнектейді. ж = f(x) (төмендегі сурет қызыл түспен) x = ажәне абсцисса осі.

Дұрыс емес интегралдар басқа шексіз интервалдар үшін де осылай анықталады:

Шексіз қисық сызықты трапеция ауданы соңғы сан болуы мүмкін, бұл жағдайда дұрыс емес интеграл жинақты деп аталады. Аудан да шексіз болуы мүмкін, бұл жағдайда дұрыс емес интеграл дивергент деп аталады.

Дұрыс емес интегралдың орнына интегралдың шегін пайдалану.Дұрыс емес интегралды есептеу үшін анықталған интегралдың шегін пайдалану керек. Егер бұл шек бар болса және ақырлы болса (шексіздікке тең емес), онда дұрыс емес интеграл жинақты деп аталады, әйтпесе ол дивергентті болады. Шектеу белгісінің астындағы айнымалының неге бейімділігі бірінші түрдегі немесе екінші түрдегі дұрыс емес интегралмен айналысатынымызға байланысты. Бұл туралы қазір білейік.

Бірінші текті дұрыс емес интегралдар – шексіз шекті және олардың жинақтылығы

Шексіз жоғарғы шегі бар дұрыс емес интегралдар

Сонымен, дұрыс емес интегралдың жазбасы әдеттегі анықталған интегралдан интегралдаудың жоғарғы шегі шексіз болуымен ерекшеленеді.

Анықтама. -ден интегралдаудың шексіз жоғарғы шегі бар бұрыс интеграл үздіксіз функция f(x) арасында а бұрын ∞ интегралдаудың жоғарғы шегімен осы функцияның интегралының шегі деп аталады б және интеграцияның төменгі шегі а интеграцияның жоғарғы шегі шексіз өскен жағдайда, яғни.

.

Егер бұл шек бар болса және шексіздікке емес, қандай да бір санға тең болса, онда дұрыс емес интеграл жинақты деп аталады, ал оның мәні ретінде шекке тең сан алынады. Әйтпесе дұрыс емес интеграл дивергент деп аталадыжәне оған ешқандай мән берілмейді.

Мысал 1. Дұрыс емес интегралды есептеңіз(егер ол жақындаса).

Шешім. Дұрыс емес интегралдың анықтамасына сүйене отырып, табамыз

Шектеу бар және 1-ге тең болғандықтан, берілген дұрыс емес интеграл жинақталадыжәне 1-ге тең.

Келесі мысалда интеграл 1-мысалдағыдай дерлік, тек х дәрежесі екі емес, альфа әрпі, ал жинақтылық үшін дұрыс емес интегралды зерттеу міндеті. Яғни, сұраққа жауап беру керек: бұл дұрыс емес интеграл альфаның қандай мәндерінде жинақталады және ол қандай мәндерде алшақтайды?

Мысал 2. Дұрыс емес интегралдың жинақтылығын зерттеңіз(төменгі интеграция шегі нөлден үлкен).

Шешім. Алдымен солай делік, содан кейін

Алынған өрнекте біз шегіне өтеміз:

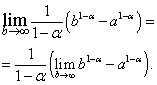
Оң жақтағы шегі бар екенін және нөлге тең болғанын көру оңай, яғни, және жоқ кезде, яғни.

Бірінші жағдайда, яғни, қашан . Егер болса, онда және жоқ.

Зерттеуіміздің қорытындысы мынадай: дұрыс емес интеграл жинақталадыжәне алшақтайдыкезінде.

Бұрыс интегралдың зерттелетін түріне Ньютон-Лейбниц формуласын қолдану , біз келесі өте ұқсас формуланы шығара аламыз:

.

Бұл жалпыланған Ньютон-Лейбниц формуласы.

Мысал 3. Дұрыс емес интегралды есептеу(егер ол жақындаса).

Бұл интегралдың шегі бар:

Бастапқы интегралды өрнектейтін қосынды болып табылатын екінші интеграл:

Бұл интегралдың шегі де бар:

.

Екі интегралдың қосындысын табамыз, ол да екі шексіз шегі бар бастапқы дұрыс емес интегралдың мәні болып табылады:

Екінші текті дұрыс емес интегралдар – шектелмеген функциялардан және олардың жинақтылығынан

Функция болсын f(x) бастап сегментіне орнатыңыз а бұрын б және оған шектеусіз. Функция нүктеде шексіздікке барады делік б , ал сегменттің барлық басқа нүктелерінде ол үздіксіз.

Анықтама. Функцияның дұрыс емес интегралы f(x) сегментінде а бұрын б интегралдаудың жоғарғы шегімен осы функцияның интегралының шегі деп аталады в , егер ұмтылған кезде в Кімге б функция шексіз және нүктеде артады x = б функциясы анықталмаған, яғни.

.

Егер бұл шек бар болса, онда екінші текті дұрыс емес интегралды конвергентті, әйтпесе дивергентті деп атайды.

Ньютон-Лейбниц формуласын қолданып, шығарамыз.

Жинақтау үшін дұрыс емес интегралдарды зерттеу мысалдары

1-мысал
.

Осылайша, бұл интеграл a > 1 үшін жинақталады және £ 1 үшін ажырайды.

2-мысал Конвергенцияны зерттеңіз. Интегралды анықтама бойынша есептейміз:
.

Осылайша, бұл интеграл а үшін жинақталады<1 и расходится при a³1.

3-мысал Конвергенцияны зерттеңіз .

<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два

.

Бірінші I1 интегралының жинақталуын эквивалентті функция арқылы зерттейміз: (өйткені n>0), ал интеграл m>-1 болғанда жинақталады (2-мысал). Сол сияқты, I2 интегралы үшін:

Ал m+n үшін интеграл жинақталады<-1 (пример2). Следовательно, исходный интеграл сходится при выполнении одновременно двух условий m>-1 және m+n<-1, и будет расходится при нарушении хотя бы одного из них.

4-мысал Конвергенцияны зерттеңіз.

Интеграл шексіз үлкен болуы мүмкін (егер m<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два:

x®0 кезінде arctgx »x болғандықтан, I1 интегралы m+1>-1 үшін жинақталатын интегралға эквивалент болады, яғни m>-2 үшін (1-мысал).

Бірінші түрдегі I2 бұрыс интегралдағы интеграл үшін эквивалентті таңдаймыз:

x® ¥ үшін arctgx » p/2 болғандықтан. Демек, екінші салыстыру критерийі бойынша I2 интегралы m + n үшін жинақталады.<-1, и расходится в противном случае.

I1 және I2 интегралдарының жинақтылық шарттарын біріктіріп, бастапқы интегралдың жинақтылығының шарттарын аламыз: m>-2 және m+n<-1 одновременно.

Түсініктеме. 2-4 мысалдарда конвергенция үшін қажетті және жеткілікті шарттарды қамтамасыз ететін 2 салыстыру критерийі қолданылды, бұл параметр мәндері бойынша белгілі бір шартта жинақтылықты орнату арқылы интегралдың алшақтығын дәлелдемеуге мүмкіндік береді. алынған конвергенция шарттары бұзылса.

5-мысал Конвергенцияны зерттеңіз.

Бұл интегралда 0 сингулярлық нүкте бар, онда интеграл p үшін шексіз бола алады.<0, поэтому снова разобьем исходный интеграл на два:

.

I1 интегралы екінші текті дұрыс емес интеграл, ал интеграл x®0 кезінде xp функциясына эквивалентті (e-x ®1 x®0 кезінде), яғни I1 p>-1 үшін жинақталады (1-мысал).

I2 интегралы бірінші текті дұрыс емес интеграл. Келесіге тең функцияны таңдаңыз интеграл, ол экспоненциалды функцияны қамтымайтындай, сәтсіз аяқталады. Сондықтан алдыңғы мысалдардағыдай 2-ші салыстыру критерийін қолдану мүмкін емес. Бірінші салыстыру критерийін қолданайық, ол үшін біз келесі белгілі фактіні қолданамыз:

a>0 және кез келген p үшін. Бұдан және xpe-ax функциясының үзіліссіз болуынан, бұл функция шектелген, яғни xpe-ax болатындай тұрақты M>0 бар.< M. Возьмем, например, a=1/2, и оценим интеграл I2 сверху:

Яғни, I2 интегралы кез келген p үшін жинақталады.

Осылайша, бастапқы интеграл p>-1 үшін жинақталады.

6-мысал Конвергенцияны зерттеңіз.

Айнымалыны өзгертейік: t = lnx, және аламыз

Интегралдың екіге бөлінуі 5-мысалдағыдай орындалады. I1 интегралы 5-мысалдағы I1 интегралына толығымен эквивалентті, сондықтан q үшін жинақталады.<1.

I2 интегралын қарастырайық. 1-б<0 этот интеграл полностью эквивалентен интегралу I2 в примере 5 (доказательство сходимости аналогично, а условие 1-p<0 нужно для выполнения және a=(1-p)/2.).

Сонымен, I2 p>1 үшін жинақталады. Бірақ бұл интегралдың жинақтылығын зерттеу аяқталмаған, өйткені пайдаланылған жинақтылық критерийі жинақтылық үшін жеткілікті шарттарды ғана береді. Сондықтан конвергенцияны 1-p £ 0 ретінде зерттеу қажет.

p=1 жағдайын қарастырайық. Сонда I2 интегралы q>1 кезінде жинақталатын (бұл жағдайда I1 интегралының алшақтатылатынын ескеріңіз) және басқаша алшақтататын -ға эквивалентті болады.

б үшін<1 оценим интеграл I2 и покажем его расходимость. Для этого вспомним, что 1-p>0 үшін, демек, кейбір A>1-ден бастап, Т- QЕ(1- П) Т³M=const>0. Сонда I2 интегралы бағалауды қанағаттандырады

,

Оң жағындағы интеграл алшақтайтын жерде, бұл I2 интегралының дивергенциясын дәлелдейді.

Алынған нәтижелерді қорытындылай келе, бастапқы интеграл q үшін жинақталатынын аламыз<1 и p>1, әйтпесе интеграл алшақтайды.

6-мысал Абсолютті және шартты жинақтылықты тексеріңіз.

Бастапқы интегралды екіге бөлейік:

.

Конвергенция. I1 интегралы мынаған эквивалент , яғни p үшін жинақталады<2 (пример 1) , причем абсолютно, так как подынтегральная функция положительна на отрезке интегрирования.

I2 интегралы p>0 үшін Дирихлет-Абель критерийіне жақындайды, өйткені антитуынды sin(x) шектелген, ал 1/xp функциясы х шексіздікке ұмтылатындықтан монотонды түрде нөлге ұмтылады.

p £ 0 үшін интегралдың ажырайтынын көрсетейік. Ол үшін Коши критерийін, дәлірек айтсақ, оны теріске шығаруды қолданамыз

.

Келесі мәндерді R1 және R2 ретінде алайық: R1=2pk және R2=2pk+p/2, содан кейін

, p>0 үшін.

Осылайша, интеграл 0-ге жинақталады

Абсолютті конвергенция I1 интегралының абсолютті жинақтылығы қазірдің өзінде орнатылған, I2 абсолютті жинақтылығын қарастырайық. Интегралды жоғарыдан есептейік:

, яғни интеграл p>1 үшін жинақталады.

p £ 1 үшін дивергенцияны дәлелдеу үшін интегралды төменнен бағалаймыз

.

Функциялар айырымының соңғы интегралын интегралдар айырымына бөлеміз

.

Егер екі интеграл да жинақталса, онда айырымның интегралы жинақталады, егер интегралдың біреуі ажыратылса, екіншісі жинақталса, онда айырымның интегралы жинақталады. Екі интегралдың да дивергенциясы болған жағдайда, айырымның интегралының жинақтылығы қосымша зерттеуге жатады. Бізді сипатталған жағдайлардың екіншісі қызықтырады.

Дивергент (1-мысал) б<1. сходится по признаку Дирихле-Абеля при 1>p>0 (Жиындықты қараңыз), демек, интеграл төменнен дивергентті интегралмен бағаланады, яғни ол дивергенцияланады.

p³1 жағдайы бізді қызықтырмайды, өйткені параметрдің осы мәндері үшін интеграл алшақтайды.

Осылайша, бастапқы интеграл абсолютті 0-ге жинақталады

Егер интегралда интегралдаудың (ақырлы) интервалында екінші текті үзіліс болса, екінші текті дұрыс емес интеграл туралы айтылады.

10.2.1 Анықтамасы және негізгі қасиеттері

$\left[ a, \, b \right ]$ интегралдау интервалын белгілейік, төменде бұл сандардың екеуі де шекті деп қабылданады. Егер тек 1 бос орын болса, ол не $a$ нүктесінде, не $b$ нүктесінде, немесе $(a,\,b)$ аралығының ішінде болуы мүмкін. Алдымен $a$ нүктесінде екінші текті үзіліс болған жағдайды, ал басқа нүктелерде интеграл үзіліссіз болатын жағдайды қарастырайық. Сондықтан біз интегралды талқылаймыз

\begin(теңдеу) I=\int _a^b f(x)\,dx, (22) \label(intr2) \end(теңдеу)

Мұндағы $f(x) \оң жақ көрсеткі \infty $ $x \оң жақ көрсеткі a+0$ болғанда. Бұрынғыдай, ең алдымен, бұл өрнекке мән беру керек. Ол үшін интегралды қарастырыңыз

\[ I(\epsilon)=\int _(a+\epsilon)^b f(x)\,dx. \]

Анықтама. Шектеу болсын

\[ A=\lim _(\epsilon \rightarrow +0)I(\epsilon)=\lim _(\epsilon \rightarrow +0)\int _(a+\epsilon)^b f(x)\,dx. \]

Сонда екінші текті дұрыс емес интеграл (22) жинақталады және оған $A$ мәні тағайындалады, $f(x)$ функциясының өзі $\left[ a, \ интервалында интегралданатын деп айтылады. , b\right]$.

Интегралдау интервалының жоғарғы шегінде интегралдың екінші түрінің үзілуі болған кездегі нұсқаны қарастырайық. Бұл жағдайды $x=-t$ айнымалысын өзгертіп, одан кейін интеграцияның шектерін қайта реттеу арқылы алдыңғы жағдайға келтіруге болады.

Интегралда $c \in (a,\,b)$ нүктесінде интегралдау интервалының ішінде екінші текті үзіліс болған жағдайды қарастырайық. Бұл жағдайда бастапқы интеграл

\begin(теңдеу) I=\int _a^bf(x)\,dx (23) \label(intr3) \end(теңдеу)

сомасы ретінде ұсынылған

\[ I=I_1+I_2, \quad I_1=\int _a^cf(x)\,dx +\int _c^df(x)\,dx. \]

Анықтама. Егер $I_1, \, I_2$ интегралдарының екеуі де жинақталса, онда дұрыс емес интеграл (23) жинақталған деп аталады және оған $I_1, \, I_2$ интегралдарының, $f(x) функциясының қосындысына тең мән беріледі. $ $\left [a, \, b\right]$ интервалында интегралданатын деп аталады. $I_1,\, I_2$ интегралдарының кем дегенде біреуі дивергентті болса, дұрыс емес интеграл (23) дивергентті деп аталады.

2-ші текті жинақтаушы бұрыс интегралдар жай анықталған интегралдардың барлық стандартты қасиеттеріне ие.

1. $f(x)$, $g(x)$ $\left[ a, \,b \right ]$ интервалында интегралданатын болса, онда олардың $f(x)+g(x)$ қосындысы сондай-ақ осы аралықта интегралды және \[ \int _a^(b)\left(f(x)+g(x)\right)dx=\int _a^(b)f(x)dx+\int _a^( b)g (x)dx. \] 2. Егер $f(x)$ $\left[ a, \, b \right ]$ интервалында интегралданатын болса, онда кез келген $C$ тұрақтысы үшін $C\cdot f(x)$ функциясы да болады. осы интервалда интегралды , және \[ \int _a^(b)C\cdot f(x)dx=C \cdot \int _a^(b)f(x)dx. \] 3. Егер $f(x)$ осы интервалда $\left[ a, \, b \right ]$ және $f(x)>0$ интервалында интегралданатын болса, онда \[ \int _a^( b ) f(x)dx\,>\,0. \] 4. Егер $f(x)$ $\left[ a, \, b \right ]$ интервалында интегралданатын болса, онда кез келген $c\in (a, \,b)$ үшін интегралдар \[ \ int _a^ (c) f(x)dx, \quad \int _c^(b) f(x)dx \] де жинақталады және \[ \int _a^(b)f(x)dx=\int _a ^(c ) f(x)dx+\int _c^(b) f(x)dx \] (интегралдың аралықтағы қосындысы).

Интегралды қарастырайық

\begin(теңдеу) I=\int _0^(1)\frac(1)(x^k)\,dx. (24) \label(mod2) \end(теңдеу)

Егер $k>0$ болса, интеграл $\infty$ $x \rightarrow +0$ түрінде болады, сондықтан интеграл екінші түрдегі дұрыс емес. Функциямен таныстырамыз

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx. \]

Бұл жағдайда антитуынды белгілі, сондықтан

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k )|_(\epsilon)^1= \frac(1)(1-k)-\frac(\epsilon ^(1-k))(1-k). \]

$k \neq 1$ үшін,

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x)\,dx\,=lnx|_(\epsilon)^1= -ln \epsilon. \]

$k = 1$ үшін. $\epsilon \rightarrow +0$ әрекетін қарастыра отырып, интеграл (20) $k үшін жинақталады деген қорытындыға келеміз.

10.2.2 2-ші түрдегі дұрыс емес интегралдарды жинақтау критерийлері

Теорема (салыстырудың бірінші белгісі). $f(x)$, $g(x)$ $x\in (a,\,b)$ және $0 үшін үздіксіз болсын 1. Егер интеграл \[ \int _a^(b)g(x) dx \] жинақталады, содан кейін \[ \int _a^(b)f(x)dx интегралы да жинақталады. \] 2. Егер \[ \int _a^(b)f(x)dx \] интегралы ауытқыса, онда \[ \int _a^(b)g(x)dx интегралы да ажырайды. \]

Теорема (салыстырудың екінші белгісі). $f(x)$, $g(x)$ $x\in (a,\,b)$ үшін үздіксіз және оң болсын және шекті шек болсын.

\[ \theta = \lim_(x \rightarrow a+0) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \]

Содан кейін интегралдар

\[ \int _a^(b)f(x)dx, \quad \int _a^(b)g(x)dx \]

бір уақытта біріктіру немесе ажырату.

1. Шектері шексіз бұрыс интегралдар

Интегралдың интегралдық қосындылардың шегі ретіндегі анықтамасын еске түсірейік:

Анықтамада интегралдау интервалы ақырлы, ал онда f (x) функциясы үзіліссіз болады. Бұл жорамалдарды бұзу дұрыс емес интегралдарға әкеледі.

Анықтама.Егер интеграл шексіз өсумен ақырлы шекке ұмтылса «б», онда бұл шек f (x) функциясының шексіз жоғарғы шекарасы бар бұрыс интеграл деп аталады және символмен белгіленеді.

Бұл жағдайда дұрыс емес интеграл бар немесе жинақталады деп аталады.

Көрсетілген шек жоқ немесе бар болса, бірақ шексіз болса, онда интеграл жоқ немесе ауытқиды деп аталады.

Шексіз төменгі шегі бар бұрыс интеграл осылай анықталады:

Екі шексіз шекарасы бар бұрыс интеграл мына формуламен анықталады:

мұндағы c – х осіндегі кез келген тұрақты нүкте.

Сонымен, бұрыс интегралдар шексіз төменгі шекпен, шексіз жоғарғы шекпен, сондай-ақ екі шексіз шекарамен болуы мүмкін.

Конвергенция белгілері. Абсолютті және шартты жинақтылық

Интеграл әрбір интеграл бар болғанда ғана бар: және .

Мысал.Интегралдың жинақтылығын зерттеңіз

c = 0 деп есептесек, мынаны аламыз:

анау. интеграл жинақталады.

Кейде дұрыс емес интегралды есептеудің қажеті жоқ, бірақ оны басқа интегралмен салыстыру арқылы жинақталатынын немесе ажырайтынын білу жеткілікті.

Дұрыс емес интегралдар үшін салыстыру теоремасы.

f (x) функциясының аралықта бірінші текті бірнеше (ақырлы сан) үзіліс нүктелері болсын, бұл «кедергі» үзіліс нүктелері бар кесіндіні бірнеше кесіндіге бөлу арқылы оңай жойылады, әрбір жеке бөлім бойынша анықталған интегралдар есептелсін. және нәтижелерді қосыңыз.

Қарастырыңыз анықталған интегралсегментінің ұштарының біріне жақындаған кезде шектелмеген функциядан, мысалы, .

(Мұндай жағдайларда әдетте: ''Функцияның интеграциялық сегменттің оң жағында шексіз үзіліс бар'' деп айтылады.)

Бұл жерде интегралдың әдеттегі анықтамасы өз мағынасын жоғалтатыны анық.

Анықтама. a £ x үшін үзіліссіз болатын f(x) функциясының бұрыс интегралы< b и неограниченной при x ® b - 0, называется предел:

Сол сияқты интервалдың сол жағында шексіз үзіліссіз функцияның дұрыс емес интегралы анықталады:

Сондықтан [ -1, 0] ауданында интеграл алшақтайды.

Бұл интегралдың кесіндіде де ажырайтынын білдіреді.

Осылайша, бұл интеграл барлық сегментте алшақтайды [-1, 1]. Назар аударыңыз, егер х = 0 нүктесіндегі интегралдың үзіліссіздігіне назар аудармай, осы интегралды есептей бастасақ, біз дұрыс емес нәтиже аламыз. Шынымен,

, бұл мүмкін емес.

Сонымен, үзіліссіз функцияның дұрыс емес интегралын зерттеу үшін оны бірнеше интегралға «бөліп», оларды зерттеу керек.