Merkkejä väärien integraalien konvergenssista. Väärät integraalit Määritelmä ja perusominaisuudet

Lause 12.11 (virheellisten integraalien vertailutesti). Olkoot funktiot f(x) ja g(x) jatkuvia välillä [a, ">) ja täyttävät sen ehdon 0 fix) ?(x). Sitten integraalin konvergenssista

seuraa integraalin konvergenssia

ja päinvastoin, integraalin (12.64) divergenssi tarkoittaa integraalin (12.63) hajoamista.

Todiste. Otetaan käyttöön merkintä:

Toiminto P(K) on ei-laskeva; itse asiassa, jos ja minä 2 sitten

J korjata) dx>0 ja sitten

Ota arvosarja (/? „) -> ">; sitten vastaava funktioarvojen sarja (F(Rn)) on monotoninen ja ei vähene. Olkoon integraali (12.63) konvergoi ja sitten sekvenssi (67 ( R se)) on rajoitettu; mutta silloin myös sarja on rajoitettu (F(/?n)) ja siten Lauseen 7.13 nojalla se konvergoi. Siksi on olemassa raja F(R) klo R-+ ">, eli integraali (12.64) konvergoi.

Todistamme nyt lauseen toisen osan; anna integraalin (12.64) hajota. Jos oletetaan, että integraali (12.63) suppenee, niin edellä todistetun mukaan integraalin (12.64) täytyy myös konvergoida, mikä on ristiriidassa ehdon kanssa. Lause on todistettu. ?

Kommentti. Samanlainen vertailukriteeri pätee myös toisen tyyppisille väärille integraaleille. Jos funktiot f(x) ja g (X) jatkuva puolivälissä [a> b) ja kaikille pisteille jossain yksittäisen pisteen naapurustossa b täyttynyt

ehdot 0 (x), niin integraalin Jg(x)dx konvergenssista seuraa, että

integraali J/(x)dx, ja integraalin J/(x)dx divergenssistä - hajonta

integraalin Jg(x)dx silta.

Tarkastellaanpa esimerkkejä väärien integraalien konvergenssin tutkimisesta.

Esimerkki 27. T . ^-.

X 3 (1 + e L)

Ratkaisu. Verrataan tässä integraalissa olevaa integrandia funktioon

Dg. On selvää, että -g--

X r* (1+0 x J

J-jdx grad konvergoi; siksi vertailukriteerin perusteella lähentyy ja 1 X

ny integraali.

Esimerkki 28. I-.

Ratkaisu. Vertaamalla tämän integraalin integradia funktioon 1/x,

näemme, että (1 + In x)/x > 1/x välillä 1

poikkeaa, joten annettu integraali poikkeaa myös vertailukriteerin perusteella.

Lopuksi esitämme ilman todisteita Cauchyn kriteerin ensimmäisen tyyppisen virheellisen integraalin konvergenssille.

12.10.4. Väärien integraalien absoluuttinen ja ehdollinen konvergenssi

Määritelmä 5. Kutsutaan väärä integraali J/(x)dx ehdottomasti

lähentyvä, jos integraali J|/(x)|dx konvergoi.

Määritelmä 6. Kutsutaan väärä integraali J /(x) dx ehdollisesti samanlainen

kytevä, jos se konvergoi ja integraali J|/(x)|dx hajoaa.

Huomaa, että integraalin absoluuttinen konvergenssi merkitsee sen konvergenssia määrätyn integraalin estimaatin 3 ja Cauchyn kriteerin perusteella.

Lause 12.13 (Dirichlet-Abel-testi*). Olkoon funktio f(x) jatkuva ja sillä on rajoitettu antiderivaata F(x) välillä [a, ">), kun taas funktiolla g(x) on jatkuva derivaatta tällä välillä, se ei kasva ja pyrkii nollaan x -> ©o. Sitten väärä integraali

lähentyy.

Todiste. Integraaliin J /(x)g(x)dx sovelletaan osien integrointia

mielivaltaisella segmentillä R R" Kanssa [ A, °°). Meillä on:

Lause 12.12. Väärän integraalin (12.64) konvergenssiin on välttämätöntä ja riittävää, että mille tahansa e > 0:lle löytyy tällainen luku A> 0, mikä tahansa R" ja /?", suurempi kuin A, seuraava epätasa-arvo pätee:

Lauseen mukaan F(x) rajoitettu, ts. |F(x)| K. Funktio g(x) ei kasva ja pyrkii nollaan x -» «>, siis. g(x)> 0 ja g"(x)

Abel Niels Henrik (1802-1829) norjalainen matemaatikko.

Koska lauseen hypoteesin mukaan g(x) -» 0 x -> ©°, mielivaltainen numero e > 0 löydät numeron A> sellainen, että klo R"> L eriarvoisuus toteutuu g(R") Korvaamalla tämän estimaatiin (12.68), saadaan:

joka vastaa Cauchyn kriteeriä integraalin (12.66) konvergenssille. Lause on todistettu. ?

Harkitse esimerkkejä Dirichlet-Abel-testin käytöstä virheellisten integraalien konvergenssiin.

Esimerkki 29. f^^dx, a > 0.

Ratkaisu. Laitamme / (x) \u003d sin x, g(x)= l/x"; on helppo varmistaa, että kaikki lauseen ehdot täyttyvät, eli tämä integraali konvergoi. Jos a > 1, tämä integraali

ral konvergoi täysin. Todellakin, |synti x/xP 1/d L, integraali J(l/x e)dx

konvergoi, ts. verrattuna (Lause 12.11), tämä integraali myös konvergoi absoluuttisesti.

Esimerkki 30. Jsin x 2 dx - Fresnel-integraali, o

Ratkaisu. Esitämme tämän integraalin summana:

Koska sin x 2 on jatkuva funktio janalla (0, 1J), ensimmäinen integraali kohdassa (12.69) on olemassa. Määrittääksemme virheellisen integraalin konvergenssin (12.69) oikealla puolella, asetamme / (x) \ u003d x sin x 2, g(x) = 1/x. Sitten funktiolle f(x) antiderivaata F(x) = -cosx 2 /! on rajoittunut väliin |1, ">), kun taas #(x) on positiivinen, pyrkii nollaan muodossa x -» °° ja sillä on jatkuva derivaatta (1, ©o). Siten Dirichlet - Abel -kriteerin mukaan toinen integraali kohdassa (12.69) konvergoi, ts. Fresnel-integraali myös konvergoi.

Ensimmäisen tyyppiset väärät integraalit. Itse asiassa tämä on sama kiinteä integraali, mutta tapauksissa, joissa integraaleilla on ääretön ylä- tai alaintegrointiraja tai molemmat integrointirajat ovat äärettömiä.

Toisen tyyppiset väärät integraalit. Itse asiassa tämä on sama määrällinen integraali, mutta tapauksissa, joissa integraali otetaan rajoittamattomista funktioista, integrandilla ei ole integrointia äärettömän janan äärellisissä pisteissä, ja se kääntyy äärettömään.

Vertailun vuoksi. Kun otettiin käyttöön määrätyn integraalin käsite, oletettiin, että funktio f(x) on jatkuva segmentillä [ a, b], ja integrointiväli on äärellinen, eli sitä rajoittavat luvut, ei ääretön. Jotkut tehtävät johtavat tarpeeseen luopua näistä rajoituksista. Näin virheelliset integraalit näkyvät.

Väärän integraalin geometrinen merkitys osoittautuu melko yksinkertaiseksi. Kun funktion kaavio y = f(x) on akselin yläpuolella Härkä, määrätty integraali ilmaisee alueen kaareva trapetsi, rajattu käyrä y = f(x) , abskissa ja ordinaatit x = a , x = b. Väärä integraali puolestaan ​​ilmaisee viivojen välissä olevan rajattoman (äärettömän) kaarevan puolisuunnikkaan alueen y = f(x) (kuvassa alla punaisella) x = a ja abskissa-akseli.

Väärät integraalit määritellään samalla tavalla muille äärettömille intervalleille:

Äärettömän kaarevan puolisuunnikkaan pinta-ala voi olla äärellinen luku, ja tässä tapauksessa väärää integraalia kutsutaan konvergentiksi. Alue voi olla myös ääretön, jolloin väärää integraalia kutsutaan divergentiksi.

Integraalin rajan käyttäminen väärän integraalin sijaan. Väärän integraalin laskemiseksi sinun on käytettävä kiinteän integraalin rajaa. Jos tämä raja on olemassa ja se on äärellinen (ei yhtä suuri kuin ääretön), niin väärää integraalia kutsutaan konvergentiksi, muuten se on divergentti. Se, mihin rajamerkin alla oleva muuttuja pyrkii, riippuu siitä, onko kyseessä ensimmäisen vai toisen tyyppinen väärä integraali. Otetaan nyt siitä selvää.

Ensimmäisen tyyppiset väärät integraalit - äärettömillä rajoilla ja niiden lähentymisellä

Väärät integraalit, joilla on ääretön yläraja

Joten väärän integraalin tietue eroaa tavallisesta määrätystä integraalista siinä, että integroinnin yläraja on ääretön.

Määritelmä. Väärä integraali, jonka integroinnin yläraja on ääretön jatkuva toiminto f(x) välillä a ennen ∞ kutsutaan tämän funktion integraalin rajaksi integroinnin ylärajan kanssa b ja integraation alaraja a edellyttäen, että integraation yläraja kasvaa loputtomasti, eli

.

Jos tämä raja on olemassa ja se on yhtä suuri kuin jokin luku, ei ääretön, niin väärää integraalia kutsutaan konvergentiksi, ja sen arvoksi otetaan rajaa vastaava luku. Muuten väärää integraalia kutsutaan divergentiksi eikä sille anneta mitään arvoa.

Esimerkki 1. Laske väärä integraali(jos se lähentyy).

Ratkaisu. Väärän integraalin määritelmän perusteella löydämme

Koska raja on olemassa ja on yhtä kuin 1, niin annettu väärä integraali konvergoi ja on yhtä suuri kuin 1.

Seuraavassa esimerkissä integrandi on lähes sama kuin esimerkissä 1, vain x:n aste ei ole kaksi, vaan kirjain alfa, ja tehtävänä on tutkia epäsopivaa integraalia konvergenssin kannalta. Eli kysymys jää vastattavaksi: millä alfa-arvoilla tämä väärä integraali konvergoi ja millä arvoilla se eroaa?

Esimerkki 2. Tutki väärän integraalin konvergenssia(alempi integrointiraja on suurempi kuin nolla).

Ratkaisu. Oletetaan ensin, että sitten

Tuloksena olevassa lausekkeessa siirrymme rajaan osoitteessa :

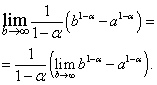
On helppo nähdä, että oikean puolen raja on olemassa ja on yhtä suuri kuin nolla, kun ts., ja ei ole olemassa, kun ts.

Ensimmäisessä tapauksessa, eli kun . Jos sitten eikä ole olemassa.

Tutkimuksemme johtopäätös on seuraava: väärä integraali konvergoi klo ja eroaa osoitteessa .

Newton-Leibnizin kaavan soveltaminen tutkittuun virheellisen integraalin tyyppiin , voimme johtaa seuraavan hyvin samanlaisen kaavan:

.

Tämä on yleistetty Newton-Leibnizin kaava.

Esimerkki 3. Laske väärä integraali(jos se lähentyy).

Tämän integraalin raja on olemassa:

Toinen integraali, joka on alkuperäistä integraalia ilmaiseva summa:

Tämän integraalin raja on myös olemassa:

.

Löydämme kahden integraalin summan, joka on myös alkuperäisen virheellisen integraalin arvo kahdella äärettömällä rajalla:

Toisen tyyppiset väärät integraalit - rajoittamattomista funktioista ja niiden lähentymisestä

Anna toiminnon f(x) asetettu segmentille alkaen a ennen b ja siihen rajattomasti. Oletetaan, että funktio menee pisteessä äärettömään b , kun taas segmentin kaikissa muissa kohdissa se on jatkuva.

Määritelmä. Toiminnon virheellinen integraali f(x) kohdasta alkaen a ennen b kutsutaan tämän funktion integraalin rajaksi integroinnin ylärajan kanssa c , jos pyrittäessä c Vastaanottaja b funktio kasvaa loputtomasti ja pisteessä x = b toimintoa ei ole määritelty, eli

.

Jos tämä raja on olemassa, niin toisen tyyppistä väärää integraalia kutsutaan konvergentiksi, muuten divergentiksi.

Newton-Leibnizin kaavaa käyttäen johdetaan.

Esimerkkejä konvergenssin sopimattomien integraalien tutkimisesta

Esimerkki 1
.

Siten tämä integraali konvergoi > 1:lle ja hajoaa £ 1:lle.

Esimerkki 2 Tutki lähentymistä. Laskemme integraalin määritelmän mukaan:
.

Siten tämä integraali konvergoi a:lle<1 и расходится при a³1.

Esimerkki 3 Tutki lähentymistä .

<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два

.

Tutkimme ensimmäisen integraalin I1 konvergenssia vastaavalla funktiolla: (koska n>0), ja integraali konvergoituu, kun m>-1 (esimerkki 2). Vastaavasti integraalille I2:

Ja integraali konvergoi m+n:lle<-1 (пример2). Следовательно, исходный интеграл сходится при выполнении одновременно двух условий m>-1 ja m+n<-1, и будет расходится при нарушении хотя бы одного из них.

Esimerkki 4 Tutki lähentymistä.

Integrandi voi olla äärettömän suuri (jos m<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два:

Koska arctgx »x kohdassa x®0, niin integraali I1 vastaa integraalia , joka konvergoi m+1>-1:lle eli m>-2:lle (esimerkki 1).

Ensimmäisen tyypin I2 virheellisen integraalin integrandille valitsemme vastaavan:

koska arctgx » p/2 for x® ¥. Siksi toisen vertailukriteerin mukaan integraali I2 konvergoi m + n:lle<-1, и расходится в противном случае.

Yhdistämällä integraalien I1 ja I2 konvergenssiehdot saadaan alkuperäisen integraalin konvergenssiehdot: m>-2 ja m+n<-1 одновременно.

Kommentti. Esimerkeissä 2-4 käytettiin 2-vertailukriteeriä, joka tarjoaa tarvittavat ja riittävät edellytykset konvergenssille, jonka avulla ei voida todistaa integraalin hajoamista asettamalla konvergenssi tietyssä ehdossa parametrien arvoille. jos saatuja konvergenssiehtoja rikotaan.

Esimerkki 5 Tutki lähentymistä.

Tämä integraali sisältää singulaaripisteen 0, jossa integrandista voi tulla ääretön p:lle<0, поэтому снова разобьем исходный интеграл на два:

.

Integraali I1 on toisen tyyppinen väärä integraali, ja integrandi on ekvivalentti kohdassa x®0 funktiolle xp (e-x®1 kohdassa x®0), eli I1 konvergoi p>-1:lle (esimerkki 1).

Integraali I2 on ensimmäisen tyyppinen virheellinen integraali. Valitse vastaava funktio integrand, joten se ei sisällä eksponentiaalista funktiota, epäonnistuu. Siksi on mahdotonta käyttää vertailukriteeriä 2, kuten edellisissä esimerkeissä. Sovelletaan ensimmäistä vertailukriteeriä, johon käytämme seuraavaa hyvin tunnettua tosiasiaa:

Jos a>0 ja mikä tahansa p. Tästä ja siitä, että funktio xpe-ax on jatkuva, seuraa, että tämä funktio on rajoitettu, eli on olemassa vakio M>0, että xpe-ax< M. Возьмем, например, a=1/2, и оценим интеграл I2 сверху:

Toisin sanoen integraali I2 konvergoi mille tahansa p:lle.

Siten alkuperäinen integraali konvergoi p>-1:lle.

Esimerkki 6 Tutki lähentymistä.

Muutetaan muuttuja: t = lnx, ja saadaan

Integraalin jakaminen kahdeksi suoritetaan samalla tavalla kuin esimerkissä 5. Integraali I1 on täysin ekvivalentti esimerkin 5 integraalin I1 kanssa ja siksi konvergoi q:lle<1.

Tarkastellaan integraalia I2 . Ellei 1-p<0 этот интеграл полностью эквивалентен интегралу I2 в примере 5 (доказательство сходимости аналогично, а условие 1-p<0 нужно для выполнения ja a=(1-p)/2.).

Joten I2 konvergoi p>1:lle. Tämä integraalin konvergenssitutkimus ei kuitenkaan ole valmis, koska käytetty konvergenssikriteeri antaa vain riittävät edellytykset konvergenssille. Siksi tarvitaan tutkimus konvergenssista 1-p £ 0.

Tarkastellaan tapausta p=1. Tällöin integraali I2 on ekvivalentti , joka konvergoi q>1:lle (huomaa, että integraali I1 hajoaa tässä tapauksessa) ja hajoaa muuten.

Sille p<1 оценим интеграл I2 и покажем его расходимость. Для этого вспомним, что Jos 1-p>0, ja siksi alkaen jostain A>1:stä, T- KE(1- P) T³M=const>0. Tällöin integraali I2 täyttää estimaatin

,

Kun oikeanpuoleinen integraali hajoaa, mikä todistaa integraalin I2 divergentin.

Summaamalla saadut tulokset saadaan, että alkuperäinen integraali konvergoi q:lle<1 и p>1, muuten integraali hajoaa.

Esimerkki 6 Tutki absoluuttista ja ehdollista konvergenssia.

Jaetaan alkuperäinen integraali kahteen osaan:

.

Lähentyminen. Integraali I1 vastaa , eli konvergoi p:lle<2 (пример 1) , причем абсолютно, так как подынтегральная функция положительна на отрезке интегрирования.

Integraali I2 konvergoi p>0:n Dirichlet-Abel-kriteerin ympärille, koska antiderivatiivinen sin(x) on rajallinen ja funktio 1/xp pyrkii monotonisesti nollaan, kun x pyrkii äärettömyyteen.

Osoitetaan, että p £ 0:lla integraali hajoaa. Tätä varten käytämme Cauchyn kriteeriä tai pikemminkin sen kieltämistä

.

Otetaan seuraavat arvot R1:ksi ja R2:ksi: R1=2pk ja R2=2pk+p/2,

, p>0.

Siten integraali konvergoi 0:aan

Absoluuttinen konvergenssi Integraalin I1 absoluuttinen konvergenssi on jo määritetty, tarkastelkaamme I2:n absoluuttista konvergenssia. Arvioidaan integraali ylhäältä:

, eli integraali konvergoi p>1:lle.

Todistaaksemme divergenssin p £ 1:lle arvioimme integraalin alhaalta

.

Jaamme funktioiden eron viimeisen integraalin integraalien erotukseksi

.

Jos molemmat integraalit suppenevat, erotuksen integraali konvergoi; jos toinen integraaleista hajoaa ja toinen konvergoi, erotuksen integraali hajoaa. Molempien integraalien hajoamisen tapauksessa erotuksen integraalin konvergenssi on lisäselvityksen kohteena. Olemme kiinnostuneita toisesta kuvatuista tapauksista.

Divergentti (esimerkki 1) s<1. сходится по признаку Дирихле-Абеля при 1>p>0 (katso Konvergenssi), joten integraali estimoidaan alhaalta divergentillä integraalilla, eli se hajoaa.

Tapaus p³1 ei kiinnosta meitä, koska integraali poikkeaa näillä parametrin arvoilla.

Siten alkuperäinen integraali konvergoi absoluuttisesti arvoon 0

Jos integrandissa on toisen tyyppinen epäjatkuvuus integraation (ääreisellä) intervallilla, puhutaan toisen tyyppisestä väärästä integraalista.

10.2.1 Määritelmä ja perusominaisuudet

Merkitään integroinnin väliä $\left[ a, \, b \right ]$, molempien näiden lukujen oletetaan olevan äärellisiä alla. Jos aukkoa on vain 1, se voi olla joko pisteessä $a$ tai pisteessä $b$ tai välin $(a,\,b)$ sisällä. Tarkastellaan ensin tapausta, jossa pisteessä $a$ on toisen tyyppinen epäjatkuvuus ja integrandi on jatkuva muissa pisteissä. Joten keskustelemme integraalista

\begin(yhtälö) I=\int _a^b f(x)\,dx, (22) \label(intr2) \end(yhtälö)

missä $f(x) \rightarrow \infty $ kun $x \rightarrow a+0$. Kuten ennenkin, ensimmäinen asia, joka on tehtävä, on antaa tälle ilmaisulle merkitys. Tätä varten harkitse integraalia

\[ I(\epsilon)=\int _(a+\epsilon)^b f(x)\,dx. \]

Määritelmä. Olkoon raja

\[ A=\lim _(\epsilon \rightarrow +0)I(\epsilon)=\lim _(\epsilon \rightarrow +0)\int _(a+\epsilon)^b f(x)\,dx. \]

Sitten toisen tyyppisen virheellisen integraalin (22) sanotaan konvergoivan ja sille annetaan arvo $A$, itse funktion $f(x)$ sanotaan olevan integroitavissa väliin $\left[ a, \ , b\right]$.

Tarkastellaan varianttia, kun integrandin toisen lajin epäjatkuvuus on integrointivälin ylärajalla. Tämä tapaus voidaan vähentää edelliseen muuttamalla muuttujaa $x=-t$ ja järjestämällä sitten integroinnin rajat uudelleen.

Tarkastellaan tapausta, jossa integrandilla on toisen tyyppinen epäjatkuvuus integrointivälin sisällä, pisteessä $c \in (a,\,b)$. Tässä tapauksessa alkuperäinen integraali

\begin(yhtälö) I=\int _a^bf(x)\,dx (23) \label(intr3) \end(yhtälö)

esitetään summana

\[ I=I_1+I_2, \quad I_1=\int _a^cf(x)\,dx +\int _c^df(x)\,dx. \]

Määritelmä. Jos molemmat integraalit $I_1, \, I_2$ konvergoivat, niin väärää integraalia (23) kutsutaan konvergentiksi ja sille annetaan arvo, joka on yhtä suuri kuin integraalien $I_1, \, I_2$ summa, funktio $f(x) $ kutsutaan integroitavaksi välissä $\left [a, \, b\right]$. Jos ainakin yksi integraaleista $I_1,\, I_2$ on divergentti, virheellisen integraalin (23) sanotaan olevan divergentti.

Suppenevilla toisen tyyppisillä epäsopivilla integraaleilla on kaikki tavallisten määrällisten integraalien standardiominaisuudet.

1. Jos $f(x)$, $g(x)$ ovat integroitavissa välille $\left[ a, \,b \right ]$, niin niiden summa $f(x)+g(x)$ on myös integroitavissa tälle aikavälille ja \[ \int _a^(b)\left(f(x)+g(x)\right)dx=\int _a^(b)f(x)dx+\int _a^( b)g (x)dx. \] 2. Jos $f(x)$ on integroitavissa väliin $\left[ a, \, b \right ]$, niin mille tahansa vakiolle $C$ on myös funktio $C\cdot f(x)$ integroitavissa tällä välillä ja \[ \int _a^(b)C\cdot f(x)dx=C \cdot \int _a^(b)f(x)dx. \] 3. Jos $f(x)$ on integroitavissa väliin $\left[ a, \, b \right ]$ ja $f(x)>0$ tällä välillä, niin \[ \int _a^( b ) f(x)dx\,>\,0. \] 4. Jos $f(x)$ on integroitavissa väliin $\left[ a, \, b \right ]$, niin minkä tahansa $c\in (a, \,b)$ integraalit \[ \ int _a^ (c) f(x)dx, \quad \int _c^(b) f(x)dx \] myös konvergoivat ja \[ \int _a^(b)f(x)dx=\int _a ^(c ) f(x)dx+\int _c^(b) f(x)dx \] (integraalin summaus välissä).

Harkitse integraalia

\begin(yhtälö) I=\int _0^(1)\frac(1)(x^k)\,dx. (24) \label(mod2) \end(yhtälö)

Jos $k>0$, integrandilla on tapana olla $\infty$ muodossa $x \rightarrow +0$, joten integraali on väärä toista lajia. Esittelemme toiminnon

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx. \]

Tässä tapauksessa antijohdannainen tunnetaan, joten

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k )|_(\epsilon)^1= \frac(1)(1-k)-\frac(\epsilon ^(1-k))(1-k). \]

$k \neq 1$,

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x)\,dx\,=lnx|_(\epsilon)^1= -ln \epsilon. \]

$k = 1$. Kun otetaan huomioon $\epsilon \rightarrow +0$ käyttäytyminen, päättelemme, että integraali (20) konvergoi $k:lle

10.2.2 Kriteerit 2. tyypin virheellisten integraalien konvergenssille

Lause (ensimmäinen vertailun merkki). Olkoon $f(x)$, $g(x)$ jatkuvia kohteille $x\in (a,\,b)$ ja $0 1. Jos integraali \[ \int _a^(b)g(x) dx \] konvergoi, niin integraali \[ \int _a^(b)f(x)dx myös konvergoi. \] 2. Jos integraali \[ \int _a^(b)f(x)dx \] hajoaa, niin integraali \[ \int _a^(b)g(x)dx myös hajoaa. \]

Lause (toinen vertailun merkki). Olkoon $f(x)$, $g(x)$ jatkuva ja positiivinen kohteelle $x\in (a,\,b)$, ja olkoon äärellinen raja

\[ \theta = \lim_(x \rightarrow a+0) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \]

Sitten integraalit

\[ \int _a^(b)f(x)dx, \quad \int _a^(b)g(x)dx \]

lähentyvät tai eroavat samaan aikaan.

1. Väärät integraalit äärettömällä rajalla

Muista integraalin määritelmä integraalisummien rajana:

Määritelmä olettaa, että integrointiväli on äärellinen ja funktio f (x) on siinä jatkuva. Näiden oletusten rikkominen johtaa vääriin integraaleihin.

Määritelmä. Jos integraali pyrkii äärelliseen rajaan, jossa on rajoittamaton kasvu "b", niin tätä rajaa kutsutaan virheelliseksi integraaliksi, jolla on funktion f (x) ääretön yläraja ja jota merkitään symbolilla

Tässä tapauksessa väärän integraalin sanotaan olevan olemassa tai suppenevan.

Jos määritettyä rajaa ei ole olemassa tai se on olemassa, mutta se on ääretön, niin integraalin sanotaan olevan olemassa tai se eroaa.

Väärä integraali äärettömän alarajan kanssa määritellään samalla tavalla:

Väärä integraali, jolla on kaksi ääretöntä rajaa, määritellään kaavalla:

missä c on mikä tahansa kiinteä piste x-akselilla.

Väärät integraalit voivat siis olla äärettömän alarajalla, äärettömällä ylärajalla ja myös kahdella äärettömällä rajalla.

Merkkejä lähentymisestä. Absoluuttinen ja ehdollinen konvergenssi

Integraali on olemassa vain, kun jokainen integraali on olemassa: ja .

Esimerkki. Tutki integraalin konvergenssia

Jos oletetaan c = 0, saamme:

nuo. integraali konvergoi.

Joskus ei tarvitse laskea epäkorkeaa integraalia, vaan riittää, kun tietää, konvergoiko vai hajoaako se vertaamalla sitä toiseen integraaliin.

Vertailulause väärille integraaleille.

Olkoon funktiolla f (x) useita (äärellisen määrän) ensimmäisen tyyppisiä epäjatkuvuuspisteitä välissä, tämä "este" voidaan helposti poistaa jakamalla epäjatkuvuuspisteitä sisältävä jana useiksi segmenteiksi, laske jokaisen erillisen osion määrälliset integraalit ja lisää tulokset.

Harkitse selvä integraali funktiosta, joka on rajoittamaton, kun lähestytään segmentin yhtä päätä, esimerkiksi .

(Tällaisissa tapauksissa yleensä sanotaan: "Funktiolla on ääretön epäjatkuvuus integrointisegmentin oikeassa päässä".)

On selvää, että tavallinen integraalin määritelmä menettää merkityksensä tässä.

Määritelmä. Funktion f(x) virheellinen integraali, joka on jatkuva £ x:lle< b и неограниченной при x ® b - 0, называется предел:

Samoin määritetään funktion virheellinen integraali, jolla on ääretön epäjatkuvuus segmentin vasemmassa päässä:

Siksi alueella [ -1, 0] integraali hajoaa.

Tämä tarkoittaa, että integraali hajoaa myös segmentillä.

Siten tämä integraali hajoaa koko segmentillä [-1, 1]. Huomaa, että jos alkaisimme laskea tätä integraalia kiinnittämättä huomiota integrandin epäjatkuvuuteen pisteessä x = 0, saisimme virheellisen tuloksen. Todella,

, mikä on mahdotonta.

Joten epäjatkuvan funktion virheellisen integraalin tutkimiseksi on välttämätöntä "murtaa" se useiksi integraaleiksi ja tutkia niitä.